Menu Close

Question-143130

Tinku Tara 0 Comments
Pin




Question Number 143130 by liberty last updated on 10/Jun/21
Commented by liberty last updated on 10/Jun/21
Answered by EDWIN88 last updated on 10/Jun/21
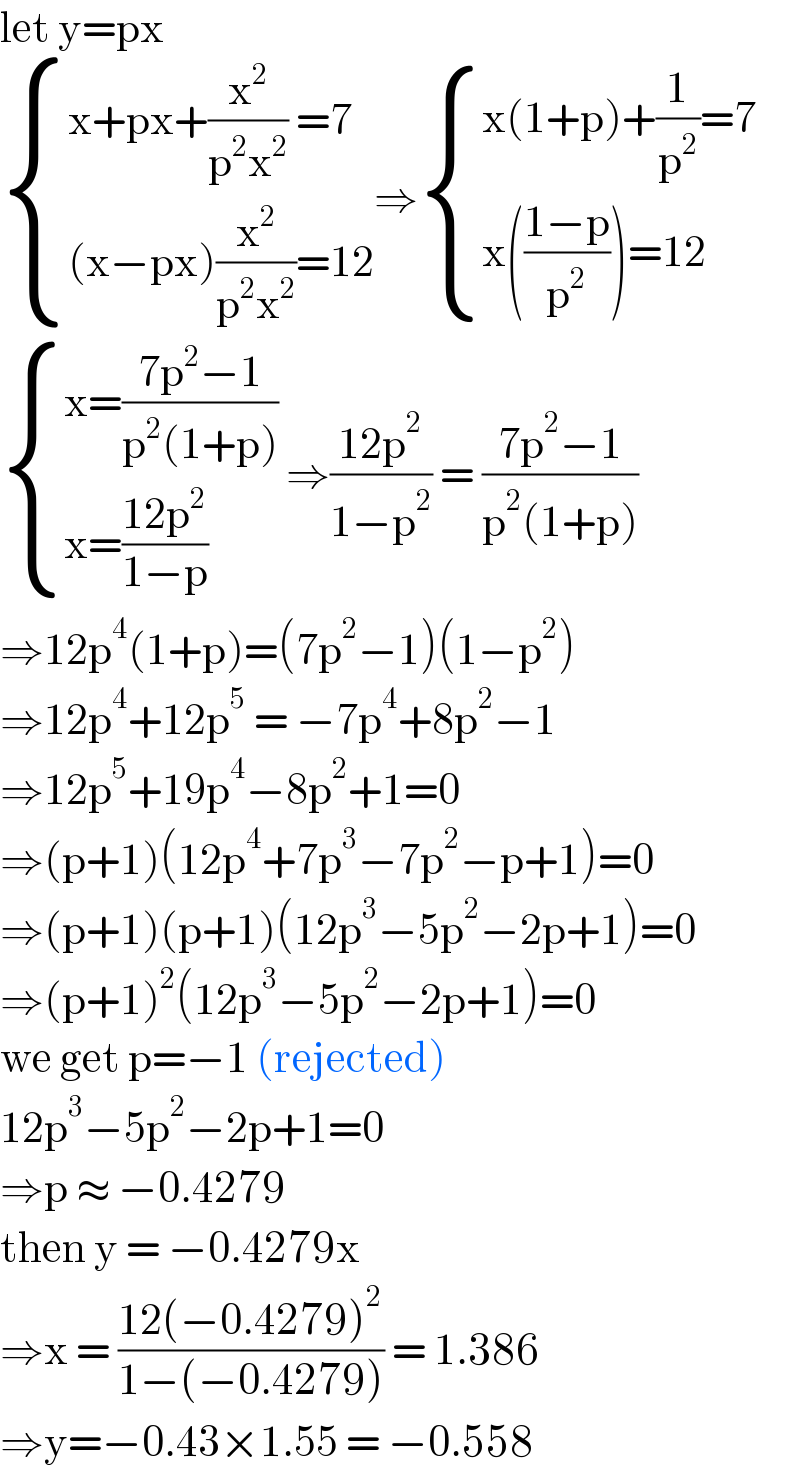
let y=px { ((x+px+(x^2 /(p^2 x^2 )) =7)),(((x−px)(x^2 /(p^2 x^2 ))=12)) :}⇒ { ((x(1+p)+(1/p^2 )=7)),((x(((1−p)/p^2 ))=12)) :} { ((x=((7p^2 −1)/(p^2 (1+p))))),((x=((12p^2 )/(1−p)))) :} ⇒((12p^2 )/(1−p^2 )) = ((7p^2 −1)/(p^2 (1+p))) ⇒12p^4 (1+p)=(7p^2 −1)(1−p^2 ) ⇒12p^4 +12p^5 = −7p^4 +8p^2 −1 ⇒12p^5 +19p^4 −8p^2 +1=0 ⇒(p+1)(12p^4 +7p^3 −7p^2 −p+1)=0 ⇒(p+1)(p+1)(12p^3 −5p^2 −2p+1)=0 ⇒(p+1)^2 (12p^3 −5p^2 −2p+1)=0 we get p=−1 (rejected) 12p^3 −5p^2 −2p+1=0 ⇒p ≈ −0.4279 then y = −0.4279x ⇒x = ((12(−0.4279)^2 )/(1−(−0.4279))) = 1.386 ⇒y=−0.43×1.55 = −0.558
$$\mathrm{let}\:\mathrm{y}=\mathrm{px} \\ $$$$\begin{cases}{\mathrm{x}+\mathrm{px}+\frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{p}^{\mathrm{2}} \mathrm{x}^{\mathrm{2}} }\:=\mathrm{7}}\\{\left(\mathrm{x}−\mathrm{px}\right)\frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{p}^{\mathrm{2}} \mathrm{x}^{\mathrm{2}} }=\mathrm{12}}\end{cases}\Rightarrow\begin{cases}{\mathrm{x}\left(\mathrm{1}+\mathrm{p}\right)+\frac{\mathrm{1}}{\mathrm{p}^{\mathrm{2}} }=\mathrm{7}}\\{\mathrm{x}\left(\frac{\mathrm{1}−\mathrm{p}}{\mathrm{p}^{\mathrm{2}} }\right)=\mathrm{12}}\end{cases} \\ $$$$\begin{cases}{\mathrm{x}=\frac{\mathrm{7p}^{\mathrm{2}} −\mathrm{1}}{\mathrm{p}^{\mathrm{2}} \left(\mathrm{1}+\mathrm{p}\right)}}\\{\mathrm{x}=\frac{\mathrm{12p}^{\mathrm{2}} }{\mathrm{1}−\mathrm{p}}}\end{cases}\:\Rightarrow\frac{\mathrm{12p}^{\mathrm{2}} }{\mathrm{1}−\mathrm{p}^{\mathrm{2}} }\:=\:\frac{\mathrm{7p}^{\mathrm{2}} −\mathrm{1}}{\mathrm{p}^{\mathrm{2}} \left(\mathrm{1}+\mathrm{p}\right)} \\ $$$$\Rightarrow\mathrm{12p}^{\mathrm{4}} \left(\mathrm{1}+\mathrm{p}\right)=\left(\mathrm{7p}^{\mathrm{2}} −\mathrm{1}\right)\left(\mathrm{1}−\mathrm{p}^{\mathrm{2}} \right) \\ $$$$\Rightarrow\mathrm{12p}^{\mathrm{4}} +\mathrm{12p}^{\mathrm{5}} \:=\:−\mathrm{7p}^{\mathrm{4}} +\mathrm{8p}^{\mathrm{2}} −\mathrm{1} \\ $$$$\Rightarrow\mathrm{12p}^{\mathrm{5}} +\mathrm{19p}^{\mathrm{4}} −\mathrm{8p}^{\mathrm{2}} +\mathrm{1}=\mathrm{0} \\ $$$$\Rightarrow\left(\mathrm{p}+\mathrm{1}\right)\left(\mathrm{12p}^{\mathrm{4}} +\mathrm{7p}^{\mathrm{3}} −\mathrm{7p}^{\mathrm{2}} −\mathrm{p}+\mathrm{1}\right)=\mathrm{0} \\ $$$$\Rightarrow\left(\mathrm{p}+\mathrm{1}\right)\left(\mathrm{p}+\mathrm{1}\right)\left(\mathrm{12p}^{\mathrm{3}} −\mathrm{5p}^{\mathrm{2}} −\mathrm{2p}+\mathrm{1}\right)=\mathrm{0} \\ $$$$\Rightarrow\left(\mathrm{p}+\mathrm{1}\right)^{\mathrm{2}} \left(\mathrm{12p}^{\mathrm{3}} −\mathrm{5p}^{\mathrm{2}} −\mathrm{2p}+\mathrm{1}\right)=\mathrm{0} \\ $$$$\mathrm{we}\:\mathrm{get}\:\mathrm{p}=−\mathrm{1}\:\left(\mathrm{rejected}\right) \\ $$$$\mathrm{12p}^{\mathrm{3}} −\mathrm{5p}^{\mathrm{2}} −\mathrm{2p}+\mathrm{1}=\mathrm{0} \\ $$$$\Rightarrow\mathrm{p}\:\approx\:−\mathrm{0}.\mathrm{4279} \\ $$$$\mathrm{then}\:\mathrm{y}\:=\:−\mathrm{0}.\mathrm{4279x} \\ $$$$\Rightarrow\mathrm{x}\:=\:\frac{\mathrm{12}\left(−\mathrm{0}.\mathrm{4279}\right)^{\mathrm{2}} }{\mathrm{1}−\left(−\mathrm{0}.\mathrm{4279}\right)}\:=\:\mathrm{1}.\mathrm{386} \\ $$$$\Rightarrow\mathrm{y}=−\mathrm{0}.\mathrm{43}×\mathrm{1}.\mathrm{55}\:=\:−\mathrm{0}.\mathrm{558} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *