Question Number 143191 by mohammad17 last updated on 11/Jun/21
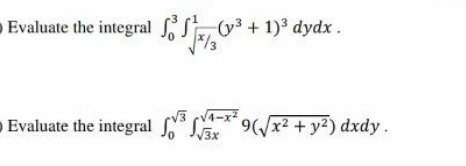
Answered by mathmax by abdo last updated on 11/Jun/21
![∫_0 ^3 ∫_(√(x/3)) ^1 (y^3 +1)^3 dydx =∫_0 ^3 (∫_(√(x/3)) ^1 (y^9 +3y^6 +3y^3 +1)dy)dx =∫_0 ^3 [(y^(10) /(10))+(3/7)y^7 +(3/4)y^4 +y]_(√(x/3)) ^1 dx =∫_0 ^3 ((1/(10))+(3/7)+(3/4)+1−(1/(10))((x/3))^5 −(3/7)((x/3))^(7/2) −(3/4)((x/3))^2 −(√(x/3)))dx =3((1/(10))+(3/7)+(3/4)+1)−(1/(10.3^5 ))∫_0 ^3 x^5 dx−(3/(7.3^(7/2) ))∫_0 ^3 x^(7/2) dx −(3/(4.3^2 ))∫_0 ^3 x^2 dx−(1/3^(1/2) )∫_0 ^3 x^(1/2) dx =(3/(10))+(9/7)+(9/4)+3−(1/(10.3^5 .6))3^6 −(3/(7.3^(7/2) .(9/2)))3^(9/2) −(3/(4.3^2 .3))3^2 −(1/(3^(1/2) .(3/2)))3^(3/2) =....](https://www.tinkutara.com/question/Q143243.png)
$$\int_{\mathrm{0}} ^{\mathrm{3}} \:\int_{\sqrt{\frac{\mathrm{x}}{\mathrm{3}}}} ^{\mathrm{1}} \:\left(\mathrm{y}^{\mathrm{3}} \:+\mathrm{1}\right)^{\mathrm{3}} \mathrm{dydx}\:=\int_{\mathrm{0}} ^{\mathrm{3}} \left(\int_{\sqrt{\frac{\mathrm{x}}{\mathrm{3}}}} ^{\mathrm{1}} \left(\mathrm{y}^{\mathrm{9}} \:+\mathrm{3y}^{\mathrm{6}} \:+\mathrm{3y}^{\mathrm{3}} \:+\mathrm{1}\right)\mathrm{dy}\right)\mathrm{dx} \\ $$$$=\int_{\mathrm{0}} ^{\mathrm{3}} \left[\frac{\mathrm{y}^{\mathrm{10}} }{\mathrm{10}}+\frac{\mathrm{3}}{\mathrm{7}}\mathrm{y}^{\mathrm{7}} \:+\frac{\mathrm{3}}{\mathrm{4}}\mathrm{y}^{\mathrm{4}} \:+\mathrm{y}\right]_{\sqrt{\frac{\mathrm{x}}{\mathrm{3}}}} ^{\mathrm{1}} \:\mathrm{dx} \\ $$$$=\int_{\mathrm{0}} ^{\mathrm{3}} \left(\frac{\mathrm{1}}{\mathrm{10}}+\frac{\mathrm{3}}{\mathrm{7}}+\frac{\mathrm{3}}{\mathrm{4}}+\mathrm{1}−\frac{\mathrm{1}}{\mathrm{10}}\left(\frac{\mathrm{x}}{\mathrm{3}}\right)^{\mathrm{5}} −\frac{\mathrm{3}}{\mathrm{7}}\left(\frac{\mathrm{x}}{\mathrm{3}}\right)^{\frac{\mathrm{7}}{\mathrm{2}}} −\frac{\mathrm{3}}{\mathrm{4}}\left(\frac{\mathrm{x}}{\mathrm{3}}\right)^{\mathrm{2}} −\sqrt{\frac{\mathrm{x}}{\mathrm{3}}}\right)\mathrm{dx} \\ $$$$=\mathrm{3}\left(\frac{\mathrm{1}}{\mathrm{10}}+\frac{\mathrm{3}}{\mathrm{7}}+\frac{\mathrm{3}}{\mathrm{4}}+\mathrm{1}\right)−\frac{\mathrm{1}}{\mathrm{10}.\mathrm{3}^{\mathrm{5}} }\int_{\mathrm{0}} ^{\mathrm{3}} \:\mathrm{x}^{\mathrm{5}} \:\mathrm{dx}−\frac{\mathrm{3}}{\mathrm{7}.\mathrm{3}^{\frac{\mathrm{7}}{\mathrm{2}}} }\int_{\mathrm{0}} ^{\mathrm{3}} \:\mathrm{x}^{\frac{\mathrm{7}}{\mathrm{2}}} \:\mathrm{dx} \\ $$$$−\frac{\mathrm{3}}{\mathrm{4}.\mathrm{3}^{\mathrm{2}} }\int_{\mathrm{0}} ^{\mathrm{3}} \:\mathrm{x}^{\mathrm{2}} \:\mathrm{dx}−\frac{\mathrm{1}}{\mathrm{3}^{\frac{\mathrm{1}}{\mathrm{2}}} }\int_{\mathrm{0}} ^{\mathrm{3}} \:\mathrm{x}^{\frac{\mathrm{1}}{\mathrm{2}}} \:\mathrm{dx} \\ $$$$=\frac{\mathrm{3}}{\mathrm{10}}+\frac{\mathrm{9}}{\mathrm{7}}+\frac{\mathrm{9}}{\mathrm{4}}+\mathrm{3}−\frac{\mathrm{1}}{\mathrm{10}.\mathrm{3}^{\mathrm{5}} .\mathrm{6}}\mathrm{3}^{\mathrm{6}} −\frac{\mathrm{3}}{\mathrm{7}.\mathrm{3}^{\frac{\mathrm{7}}{\mathrm{2}}} .\frac{\mathrm{9}}{\mathrm{2}}}\mathrm{3}^{\frac{\mathrm{9}}{\mathrm{2}}} \\ $$$$−\frac{\mathrm{3}}{\mathrm{4}.\mathrm{3}^{\mathrm{2}} .\mathrm{3}}\mathrm{3}^{\mathrm{2}} −\frac{\mathrm{1}}{\mathrm{3}^{\frac{\mathrm{1}}{\mathrm{2}}} .\frac{\mathrm{3}}{\mathrm{2}}}\mathrm{3}^{\frac{\mathrm{3}}{\mathrm{2}}} =…. \\ $$
