Question-143332

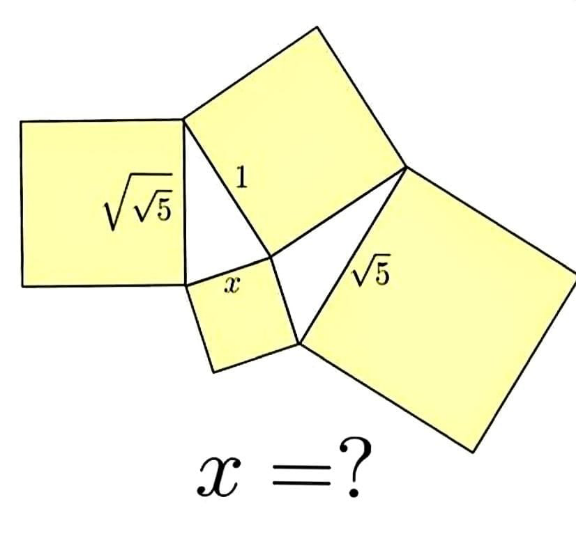
Question Number 143332 by bramlexs22 last updated on 13/Jun/21

Commented by soumyasaha last updated on 13/Jun/21

$$\:\mathrm{x}\:=\:\sqrt{\frac{\mathrm{3}+\sqrt{\mathrm{5}}}{\mathrm{2}}} \\ $$

Commented by mr W last updated on 13/Jun/21

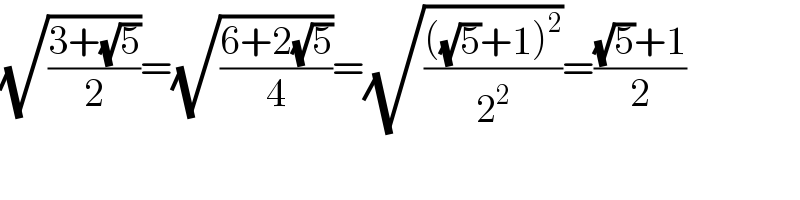
(√((3+(√5))/2))=(√((6+2(√5))/4))=(√((((√5)+1)^2 )/2^2 ))=(((√5)+1)/2)

$$\sqrt{\frac{\mathrm{3}+\sqrt{\mathrm{5}}}{\mathrm{2}}}=\sqrt{\frac{\mathrm{6}+\mathrm{2}\sqrt{\mathrm{5}}}{\mathrm{4}}}=\sqrt{\frac{\left(\sqrt{\mathrm{5}}+\mathrm{1}\right)^{\mathrm{2}} }{\mathrm{2}^{\mathrm{2}} }}=\frac{\sqrt{\mathrm{5}}+\mathrm{1}}{\mathrm{2}} \\ $$

Answered by nimnim last updated on 13/Jun/21

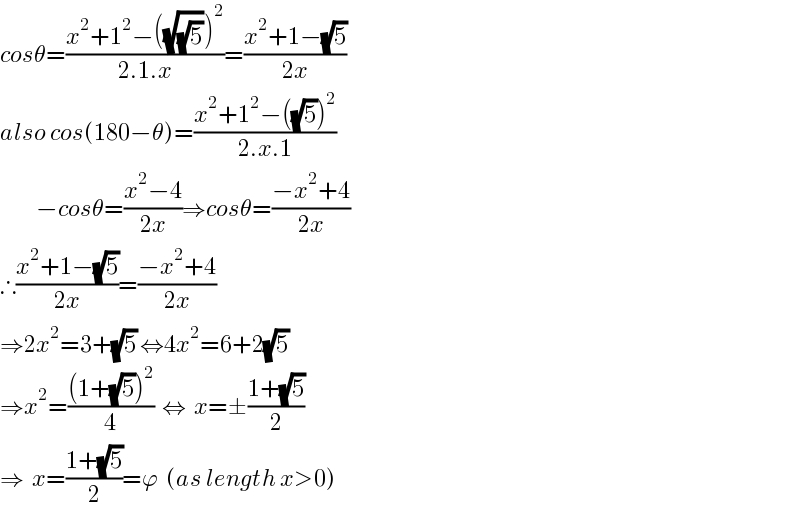
cosθ=((x^2 +1^2 −((√(√5)))^2 )/(2.1.x))=((x^2 +1−(√5))/(2x)) also cos(180−θ)=((x^2 +1^2 −((√5))^2 )/(2.x.1)) −cosθ=((x^2 −4)/(2x))⇒cosθ=((−x^2 +4)/(2x)) ∴((x^2 +1−(√5))/(2x))=((−x^2 +4)/(2x)) ⇒2x^2 =3+(√5) ⇔4x^2 =6+2(√5) ⇒x^2 =(((1+(√5))^2 )/4) ⇔ x=±((1+(√5))/2) ⇒ x=((1+(√5))/2)=ϕ (as length x>0)

$${cos}\theta=\frac{{x}^{\mathrm{2}} +\mathrm{1}^{\mathrm{2}} −\left(\sqrt{\sqrt{\mathrm{5}}}\right)^{\mathrm{2}} }{\mathrm{2}.\mathrm{1}.{x}}=\frac{{x}^{\mathrm{2}} +\mathrm{1}−\sqrt{\mathrm{5}}}{\mathrm{2}{x}} \\ $$$${also}\:{cos}\left(\mathrm{180}−\theta\right)=\frac{{x}^{\mathrm{2}} +\mathrm{1}^{\mathrm{2}} −\left(\sqrt{\mathrm{5}}\right)^{\mathrm{2}} }{\mathrm{2}.{x}.\mathrm{1}} \\ $$$$\:\:\:\:\:\:\:\:\:−{cos}\theta=\frac{{x}^{\mathrm{2}} −\mathrm{4}}{\mathrm{2}{x}}\Rightarrow{cos}\theta=\frac{−{x}^{\mathrm{2}} +\mathrm{4}}{\mathrm{2}{x}} \\ $$$$\therefore\frac{{x}^{\mathrm{2}} +\mathrm{1}−\sqrt{\mathrm{5}}}{\mathrm{2}{x}}=\frac{−{x}^{\mathrm{2}} +\mathrm{4}}{\mathrm{2}{x}} \\ $$$$\Rightarrow\mathrm{2}{x}^{\mathrm{2}} =\mathrm{3}+\sqrt{\mathrm{5}}\:\Leftrightarrow\mathrm{4}{x}^{\mathrm{2}} =\mathrm{6}+\mathrm{2}\sqrt{\mathrm{5}} \\ $$$$\Rightarrow{x}^{\mathrm{2}} =\frac{\left(\mathrm{1}+\sqrt{\mathrm{5}}\right)^{\mathrm{2}} }{\mathrm{4}}\:\:\Leftrightarrow\:\:{x}=\pm\frac{\mathrm{1}+\sqrt{\mathrm{5}}}{\mathrm{2}} \\ $$$$\Rightarrow\:\:{x}=\frac{\mathrm{1}+\sqrt{\mathrm{5}}}{\mathrm{2}}=\varphi\:\:\left({as}\:{length}\:{x}>\mathrm{0}\right) \\ $$

Commented by nimnim last updated on 13/Jun/21

Answered by mr W last updated on 13/Jun/21

Commented by mr W last updated on 13/Jun/21

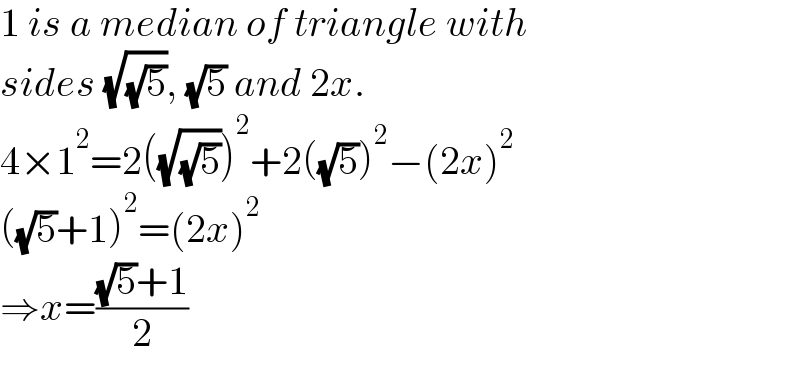
1 is a median of triangle with sides (√(√5)), (√5) and 2x. 4×1^2 =2((√(√5)))^2 +2((√5))^2 −(2x)^2 ((√5)+1)^2 =(2x)^2 ⇒x=(((√5)+1)/2)

$$\mathrm{1}\:{is}\:{a}\:{median}\:{of}\:{triangle}\:{with} \\ $$$${sides}\:\sqrt{\sqrt{\mathrm{5}}},\:\sqrt{\mathrm{5}}\:{and}\:\mathrm{2}{x}. \\ $$$$\mathrm{4}×\mathrm{1}^{\mathrm{2}} =\mathrm{2}\left(\sqrt{\sqrt{\mathrm{5}}}\right)^{\mathrm{2}} +\mathrm{2}\left(\sqrt{\mathrm{5}}\right)^{\mathrm{2}} −\left(\mathrm{2}{x}\right)^{\mathrm{2}} \\ $$$$\left(\sqrt{\mathrm{5}}+\mathrm{1}\right)^{\mathrm{2}} =\left(\mathrm{2}{x}\right)^{\mathrm{2}} \\ $$$$\Rightarrow{x}=\frac{\sqrt{\mathrm{5}}+\mathrm{1}}{\mathrm{2}} \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply