Question Number 143418 by help last updated on 14/Jun/21

Answered by physicstutes last updated on 14/Jun/21
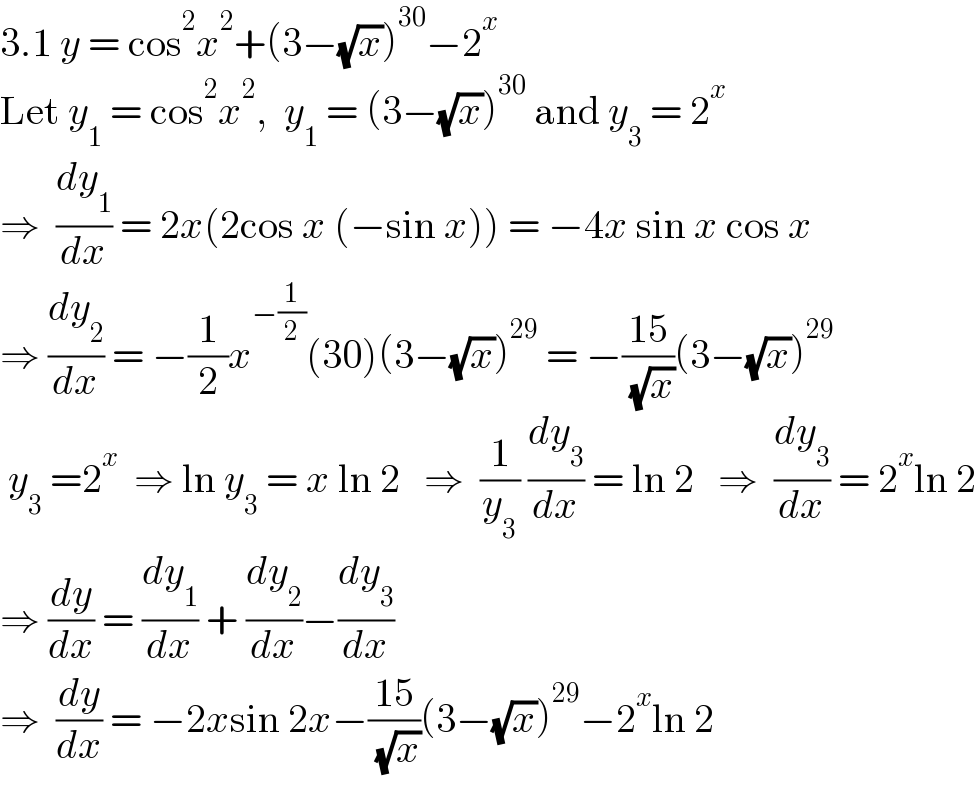
$$\mathrm{3}.\mathrm{1}\:{y}\:=\:\mathrm{cos}^{\mathrm{2}} {x}^{\mathrm{2}} +\left(\mathrm{3}−\sqrt{{x}}\right)^{\mathrm{30}} −\mathrm{2}^{{x}} \\ $$$$\mathrm{Let}\:{y}_{\mathrm{1}} \:=\:\mathrm{cos}^{\mathrm{2}} {x}^{\mathrm{2}} ,\:\:{y}_{\mathrm{1}} \:=\:\left(\mathrm{3}−\sqrt{{x}}\right)^{\mathrm{30}} \:\mathrm{and}\:{y}_{\mathrm{3}} \:=\:\mathrm{2}^{{x}} \\ $$$$\Rightarrow\:\:\frac{{dy}_{\mathrm{1}} }{{dx}}\:=\:\mathrm{2}{x}\left(\mathrm{2cos}\:{x}\:\left(−\mathrm{sin}\:{x}\right)\right)\:=\:−\mathrm{4}{x}\:\mathrm{sin}\:{x}\:\mathrm{cos}\:{x} \\ $$$$\Rightarrow\:\frac{{dy}_{\mathrm{2}} }{{dx}}\:=\:−\frac{\mathrm{1}}{\mathrm{2}}{x}^{−\frac{\mathrm{1}}{\mathrm{2}}} \left(\mathrm{30}\right)\left(\mathrm{3}−\sqrt{{x}}\right)^{\mathrm{29}} \:=\:−\frac{\mathrm{15}}{\:\sqrt{{x}}}\left(\mathrm{3}−\sqrt{{x}}\right)^{\mathrm{29}} \\ $$$$\:{y}_{\mathrm{3}} \:=\mathrm{2}^{{x}} \:\:\Rightarrow\:\mathrm{ln}\:{y}_{\mathrm{3}} \:=\:{x}\:\mathrm{ln}\:\mathrm{2}\:\:\:\Rightarrow\:\:\frac{\mathrm{1}}{{y}_{\mathrm{3}} }\:\frac{{dy}_{\mathrm{3}} }{{dx}}\:=\:\mathrm{ln}\:\mathrm{2}\:\:\:\Rightarrow\:\:\frac{{dy}_{\mathrm{3}} }{{dx}}\:=\:\mathrm{2}^{{x}} \mathrm{ln}\:\mathrm{2} \\ $$$$\Rightarrow\:\frac{{dy}}{{dx}}\:=\:\frac{{dy}_{\mathrm{1}} }{{dx}}\:+\:\frac{{dy}_{\mathrm{2}} }{{dx}}−\frac{{dy}_{\mathrm{3}} }{{dx}} \\ $$$$\Rightarrow\:\:\frac{{dy}}{{dx}}\:=\:−\mathrm{2}{x}\mathrm{sin}\:\mathrm{2}{x}−\frac{\mathrm{15}}{\:\sqrt{{x}}}\left(\mathrm{3}−\sqrt{{x}}\right)^{\mathrm{29}} −\mathrm{2}^{{x}} \mathrm{ln}\:\mathrm{2} \\ $$
