Question Number 143435 by nitu last updated on 14/Jun/21

Commented by mr W last updated on 14/Jun/21
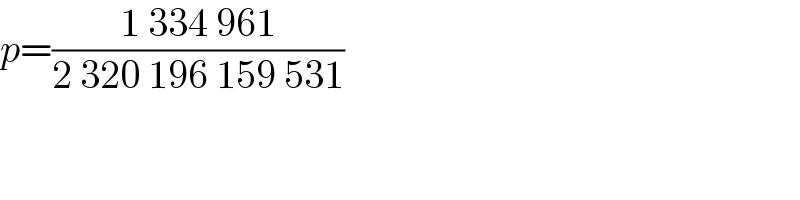
$${p}=\frac{\mathrm{1}\:\mathrm{334}\:\mathrm{961}}{\mathrm{2}\:\mathrm{320}\:\mathrm{196}\:\mathrm{159}\:\mathrm{531}} \\ $$
Commented by nitu last updated on 15/Jun/21

$$\mathrm{can}\:\mathrm{you}\:\mathrm{show}\:\mathrm{the}\:\mathrm{process}\:\mathrm{please} \\ $$
Commented by mr W last updated on 15/Jun/21

$${to}\:{form}\:\mathrm{10}\:{pairs}\:{from}\:\mathrm{20}\:{players} \\ $$$${there}\:{are}\:{totally}\:\frac{\mathrm{20}!}{\left(\mathrm{2}!\right)^{\mathrm{10}} }\:{ways}. \\ $$$${to}\:{select}\:\mathrm{10}\:{players},\:{one}\:{from}\:{each} \\ $$$${college},\:{there}\:{are}\:\mathrm{2}^{\mathrm{10}} \:{ways},\:{and}\:{to} \\ $$$${arrange}\:{the}\:{remaining}\:\mathrm{10}\:{players} \\ $$$${such}\:{that}\:{two}\:{players}\:{from}\:{the}\:{same} \\ $$$${college}\:{are}\:{not}\:{in}\:{the}\:{same}\:{pair},\:{there} \\ $$$${are}\:!\mathrm{10}\:{ways}.\:{so}\:{the}\:{answer}\:{is} \\ $$$${p}=\frac{\mathrm{2}^{\mathrm{10}} ×!\mathrm{10}}{\frac{\mathrm{20}!}{\left(\mathrm{2}!\right)^{\mathrm{10}} }}=\frac{\mathrm{2}^{\mathrm{20}} ×!\mathrm{10}}{\mathrm{20}!} \\ $$$${with}\:!\mathrm{10}=\mathrm{1334961} \\ $$$${i}'{m}\:{not}\:{sure}\:{if}\:{this}\:{answer}\:{is}\:{correct}. \\ $$$${if}\:{you}\:{have}\:{the}\:{right}\:{answer},\:{please} \\ $$$${share}\:{it}. \\ $$
Commented by nitu last updated on 17/Jun/21
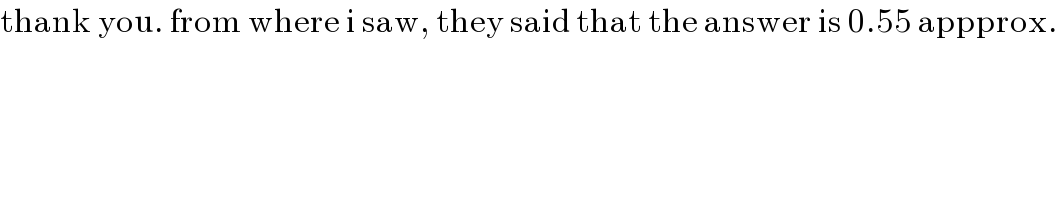
$$\mathrm{thank}\:\mathrm{you}.\:\mathrm{from}\:\mathrm{where}\:\mathrm{i}\:\mathrm{saw},\:\mathrm{they}\:\mathrm{said}\:\mathrm{that}\:\mathrm{the}\:\mathrm{answer}\:\mathrm{is}\:\mathrm{0}.\mathrm{55}\:\mathrm{appprox}.\: \\ $$
Commented by mr W last updated on 17/Jun/21

$${i}'{ll}\:{try}\:{again}… \\ $$
