Question Number 143570 by cesarL last updated on 15/Jun/21

Answered by Ar Brandon last updated on 15/Jun/21
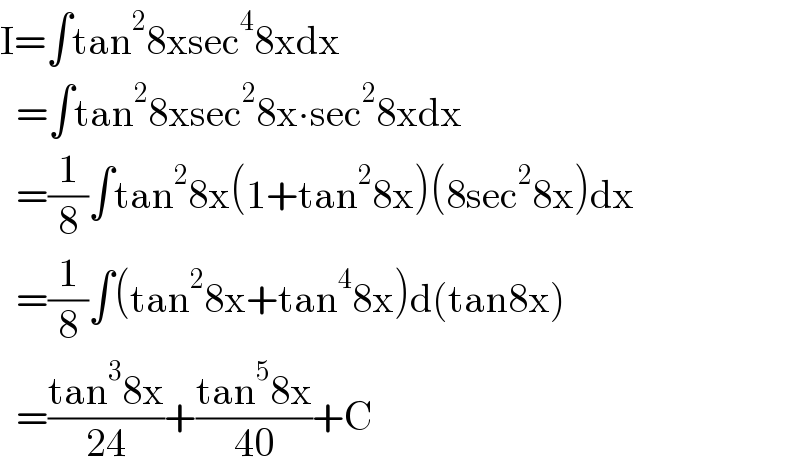
$$\mathrm{I}=\int\mathrm{tan}^{\mathrm{2}} \mathrm{8xsec}^{\mathrm{4}} \mathrm{8xdx} \\ $$$$\:\:=\int\mathrm{tan}^{\mathrm{2}} \mathrm{8xsec}^{\mathrm{2}} \mathrm{8x}\centerdot\mathrm{sec}^{\mathrm{2}} \mathrm{8xdx} \\ $$$$\:\:=\frac{\mathrm{1}}{\mathrm{8}}\int\mathrm{tan}^{\mathrm{2}} \mathrm{8x}\left(\mathrm{1}+\mathrm{tan}^{\mathrm{2}} \mathrm{8x}\right)\left(\mathrm{8sec}^{\mathrm{2}} \mathrm{8x}\right)\mathrm{dx} \\ $$$$\:\:=\frac{\mathrm{1}}{\mathrm{8}}\int\left(\mathrm{tan}^{\mathrm{2}} \mathrm{8x}+\mathrm{tan}^{\mathrm{4}} \mathrm{8x}\right)\mathrm{d}\left(\mathrm{tan8x}\right) \\ $$$$\:\:=\frac{\mathrm{tan}^{\mathrm{3}} \mathrm{8x}}{\mathrm{24}}+\frac{\mathrm{tan}^{\mathrm{5}} \mathrm{8x}}{\mathrm{40}}+\mathrm{C} \\ $$
