Question Number 143606 by bobhans last updated on 16/Jun/21
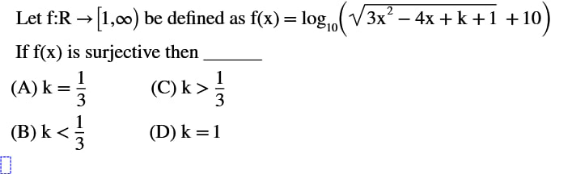
Answered by TheHoneyCat last updated on 16/Jun/21

$${f}\:\mathrm{surjective}\:\Leftrightarrow\:\:\left[\mathrm{1},\:+\infty\left[\subset{f}\left(\mathbb{R}\right)\right.\right. \\ $$$$ \\ $$$$\mathrm{knowing}\:\mathrm{that}\:{f}\in\mathscr{C}^{\mathrm{0}} \left(\mathbb{R},\left[\mathrm{1},+\infty\left[\right)\right.\right. \\ $$$$\mathrm{and}\:\mathrm{that}\:\:{f}\left({x}\right)\underset{{x}\rightarrow\mp\infty} {\rightarrow}+\infty \\ $$$$\forall{y}\in\mathbb{R}\:\:\:\:\:\:\:\:\exists{x}\mid{f}\left({x}\right)={y}\Rightarrow\left[{y},+\infty\left[\subset{f}\left(\mathbb{R}\right)\right.\right. \\ $$$$ \\ $$$$\mathrm{therefore}: \\ $$$${f}\:\mathrm{surjective}\:\Leftrightarrow\:\exists{x}\in\mathbb{R}\mid{f}\left({x}\right)=\mathrm{1} \\ $$$$\Leftrightarrow\exists{x}\in\mathbb{R}\mid\mathrm{log}_{\mathrm{10}} \left(\sqrt{\mathrm{3}{x}^{\mathrm{2}} −\mathrm{4}{x}+\mathrm{k}+\mathrm{1}}+\mathrm{10}\right)=\mathrm{1} \\ $$$$\Leftrightarrow\exists{x}\in\mathbb{R}\mid\sqrt{\mathrm{3}{x}^{\mathrm{2}} −\mathrm{4}{x}+\mathrm{k}+\mathrm{1}}+\mathrm{10}=\mathrm{10}^{\mathrm{1}} =\mathrm{10} \\ $$$$\Leftrightarrow\exists{x}\in\mathbb{R}\mid\sqrt{\mathrm{3}{x}^{\mathrm{2}} −\mathrm{4}{x}+\mathrm{k}+\mathrm{1}}=\mathrm{0} \\ $$$$\mathrm{knowing}\:\mathrm{that}\:{f}\:\mathrm{must}\:\mathrm{be}\:\mathrm{well}\:\mathrm{defined},\:\mathrm{there}\:\mathrm{can}\:\mathrm{only}\:\mathrm{be}\:\mathrm{one}\:\mathrm{such}\:{x} \\ $$$$\mathrm{otherwise},\:\mathrm{the}\:\mathrm{values}\:\mathrm{of}\:\mathrm{3X}^{\mathrm{2}} −\mathrm{4X}+\mathrm{k}+\mathrm{1}\:\mathrm{inbetween}\:\mathrm{would}\:\mathrm{be}\:\mathrm{negative} \\ $$$$ \\ $$$$\mathrm{thus}: \\ $$$${f}\:\mathrm{surjective}\:\mathrm{and}\:\mathrm{well}\:\mathrm{defined} \\ $$$$\Leftrightarrow\exists!{x}\in\mathbb{R}\mid\mathrm{3}{x}^{\mathrm{2}} −\mathrm{4}{x}+\mathrm{k}+\mathrm{1}=\mathrm{0} \\ $$$$\Leftrightarrow\mathrm{4}^{\mathrm{2}} −\mathrm{4}×\mathrm{3}×\left(\mathrm{k}+\mathrm{1}\right)=\mathrm{0} \\ $$$$\Leftrightarrow\mathrm{4}−\mathrm{3}\left(\mathrm{k}+\mathrm{1}\right)=\mathrm{0} \\ $$$$\Leftrightarrow\mathrm{k}+\mathrm{1}=\frac{\mathrm{4}}{\mathrm{3}} \\ $$$$\Leftrightarrow\mathrm{k}=\:\frac{\mathrm{1}}{\mathrm{3}}\:_{\blacksquare} \\ $$$$ \\ $$$$\mathrm{Answer}\:\left(\mathrm{A}\right) \\ $$
