Question-143633

Question Number 143633 by Niiicooooo last updated on 16/Jun/21

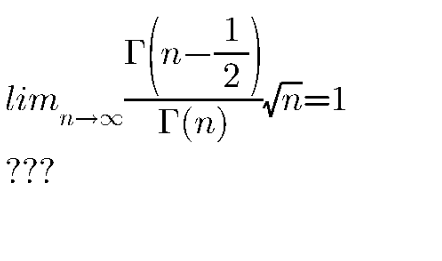
Answered by mathmax by abdo last updated on 16/Jun/21

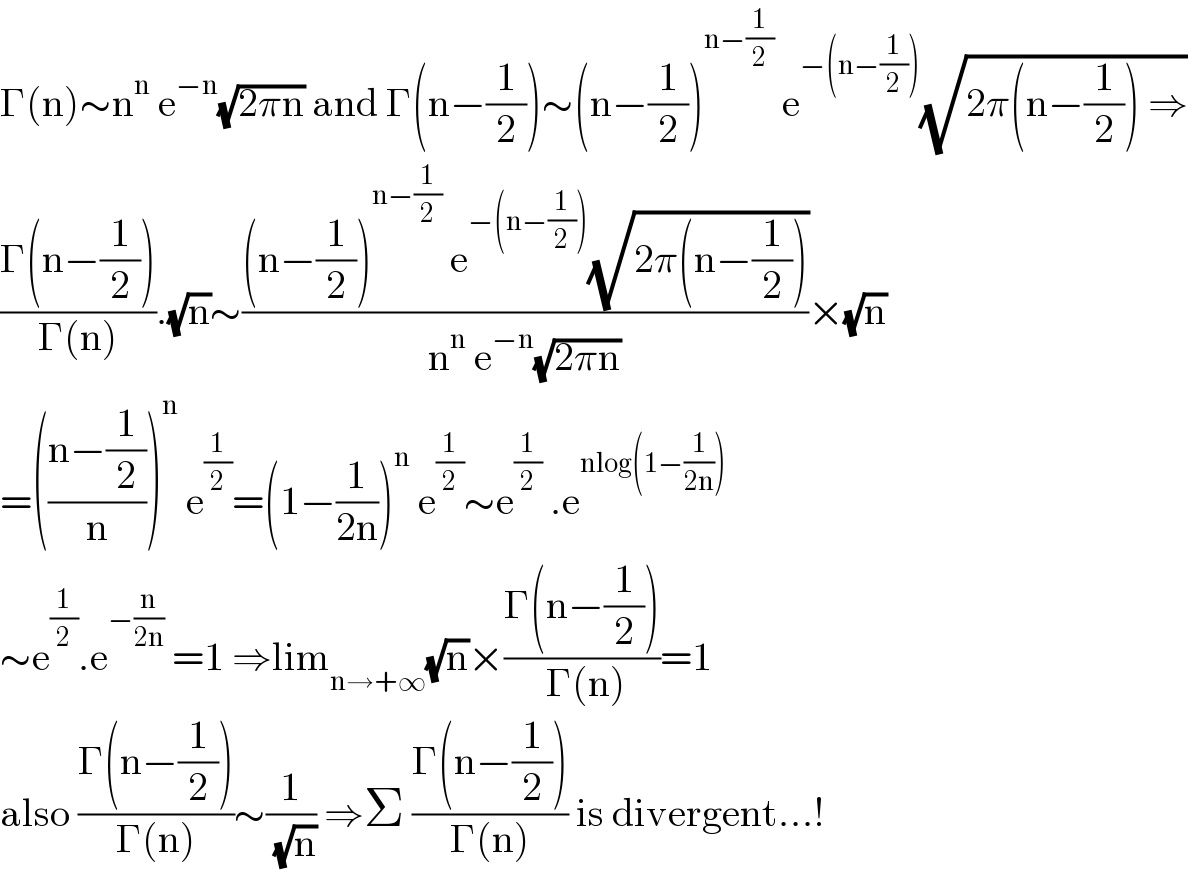
Γ(n)∼n^n e^(−n) (√(2πn)) and Γ(n−(1/2))∼(n−(1/2))^(n−(1/2)) e^(−(n−(1/2))) (√(2π(n−(1/2)) ⇒)) ((Γ(n−(1/2)))/(Γ(n))).(√n)∼(((n−(1/2))^(n−(1/2)) e^(−(n−(1/2))) (√(2π(n−(1/2)))))/(n^n e^(−n) (√(2πn))))×(√n) =(((n−(1/2))/n))^n e^(1/2) =(1−(1/(2n)))^n e^(1/2) ∼e^(1/2) .e^(nlog(1−(1/(2n)))) ∼e^(1/2) .e^(−(n/(2n))) =1 ⇒lim_(n→+∞) (√n)×((Γ(n−(1/2)))/( Γ(n)))=1 also ((Γ(n−(1/2)))/(Γ(n)))∼(1/( (√n))) ⇒Σ ((Γ(n−(1/2)))/(Γ(n))) is divergent...!

$$\Gamma\left(\mathrm{n}\right)\sim\mathrm{n}^{\mathrm{n}} \:\mathrm{e}^{−\mathrm{n}} \sqrt{\mathrm{2}\pi\mathrm{n}}\:\mathrm{and}\:\Gamma\left(\mathrm{n}−\frac{\mathrm{1}}{\mathrm{2}}\right)\sim\left(\mathrm{n}−\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{n}−\frac{\mathrm{1}}{\mathrm{2}}} \:\mathrm{e}^{−\left(\mathrm{n}−\frac{\mathrm{1}}{\mathrm{2}}\right)} \sqrt{\mathrm{2}\pi\left(\mathrm{n}−\frac{\mathrm{1}}{\mathrm{2}}\right)\:\Rightarrow} \\ $$$$\frac{\Gamma\left(\mathrm{n}−\frac{\mathrm{1}}{\mathrm{2}}\right)}{\Gamma\left(\mathrm{n}\right)}.\sqrt{\mathrm{n}}\sim\frac{\left(\mathrm{n}−\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{n}−\frac{\mathrm{1}}{\mathrm{2}}} \:\mathrm{e}^{−\left(\mathrm{n}−\frac{\mathrm{1}}{\mathrm{2}}\right)} \sqrt{\mathrm{2}\pi\left(\mathrm{n}−\frac{\mathrm{1}}{\mathrm{2}}\right)}}{\mathrm{n}^{\mathrm{n}} \:\mathrm{e}^{−\mathrm{n}} \sqrt{\mathrm{2}\pi\mathrm{n}}}×\sqrt{\mathrm{n}} \\ $$$$=\left(\frac{\mathrm{n}−\frac{\mathrm{1}}{\mathrm{2}}}{\mathrm{n}}\right)^{\mathrm{n}} \:\mathrm{e}^{\frac{\mathrm{1}}{\mathrm{2}}} =\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2n}}\right)^{\mathrm{n}} \:\mathrm{e}^{\frac{\mathrm{1}}{\mathrm{2}}} \sim\mathrm{e}^{\frac{\mathrm{1}}{\mathrm{2}}} \:.\mathrm{e}^{\mathrm{nlog}\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2n}}\right)} \\ $$$$\sim\mathrm{e}^{\frac{\mathrm{1}}{\mathrm{2}}} .\mathrm{e}^{−\frac{\mathrm{n}}{\mathrm{2n}}} \:=\mathrm{1}\:\Rightarrow\mathrm{lim}_{\mathrm{n}\rightarrow+\infty} \sqrt{\mathrm{n}}×\frac{\Gamma\left(\mathrm{n}−\frac{\mathrm{1}}{\mathrm{2}}\right)}{\:\Gamma\left(\mathrm{n}\right)}=\mathrm{1} \\ $$$$\mathrm{also}\:\frac{\Gamma\left(\mathrm{n}−\frac{\mathrm{1}}{\mathrm{2}}\right)}{\Gamma\left(\mathrm{n}\right)}\sim\frac{\mathrm{1}}{\:\sqrt{\mathrm{n}}}\:\Rightarrow\Sigma\:\frac{\Gamma\left(\mathrm{n}−\frac{\mathrm{1}}{\mathrm{2}}\right)}{\Gamma\left(\mathrm{n}\right)}\:\mathrm{is}\:\mathrm{divergent}…! \\ $$

Commented by Niiicooooo last updated on 17/Jun/21

$${Thanks}\:{sir}! \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply