Menu Close

Question-143769

Tinku Tara 0 Comments
Pin




Question Number 143769 by bemath last updated on 18/Jun/21
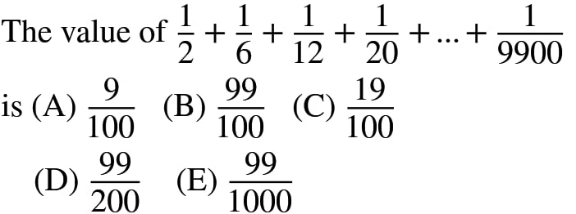
Answered by TheHoneyCat last updated on 18/Jun/21
(1/2)+(1/6)+(1/(12))+(1/(20))+(1/(9900))=((7921)/(990))≈0.8001010101 IF ′′+...+′′, in your question, is a finite sum of positive real numbers: (1) (9/(100))=0.09<0.8 ⇒ (A) is false ((19)/(100))=0.19<0.8 ⇒ (C) is false ((99)/(200))=0.495<0.8 ⇒ (D) is false ((99)/(1000))=>0.099<0.8 ⇒ (E) is false IF the right result is necessarly among {(A),(B),(C),(D),(E)} (2) well the answere is (B) however I don′t see why these two hypothesis are true. usualy ′′+...+′′ refers to an obvious sequence like, for instance, (1/2)+(1/6)+(1/(24))+... is (1/(n!)) and (1/2)+(1/6)+(1/(30))+(1/(210))+...=(1/(Π_(k=1) ^n p_n )) where p_n is the n^(th) prime number in this case, I don′t know what +...+ refers too. so obviously my proof is a bit lame
$$\frac{\mathrm{1}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{6}}+\frac{\mathrm{1}}{\mathrm{12}}+\frac{\mathrm{1}}{\mathrm{20}}+\frac{\mathrm{1}}{\mathrm{9900}}=\frac{\mathrm{7921}}{\mathrm{990}}\approx\mathrm{0}.\mathrm{8001010101} \\ $$$$ \\ $$$$\mathrm{IF}\:''+…+'',\:\mathrm{in}\:\mathrm{your}\:\mathrm{question},\:\mathrm{is}\:\mathrm{a}\:\mathrm{finite}\:\mathrm{sum}\:\mathrm{of}\:\mathrm{positive}\:\mathrm{real}\:\mathrm{numbers}:\:\left(\mathrm{1}\right) \\ $$$$\frac{\mathrm{9}}{\mathrm{100}}=\mathrm{0}.\mathrm{09}<\mathrm{0}.\mathrm{8}\:\Rightarrow\:\left(\mathrm{A}\right)\:\mathrm{is}\:\mathrm{false} \\ $$$$\frac{\mathrm{19}}{\mathrm{100}}=\mathrm{0}.\mathrm{19}<\mathrm{0}.\mathrm{8}\:\Rightarrow\:\left(\mathrm{C}\right)\:\mathrm{is}\:\mathrm{false} \\ $$$$\frac{\mathrm{99}}{\mathrm{200}}=\mathrm{0}.\mathrm{495}<\mathrm{0}.\mathrm{8}\:\Rightarrow\:\left(\mathrm{D}\right)\:\mathrm{is}\:\mathrm{false} \\ $$$$\frac{\mathrm{99}}{\mathrm{1000}}=>\mathrm{0}.\mathrm{099}<\mathrm{0}.\mathrm{8}\:\Rightarrow\:\left(\mathrm{E}\right)\:\mathrm{is}\:\mathrm{false} \\ $$$$ \\ $$$$\mathrm{IF}\:\mathrm{the}\:\mathrm{right}\:\mathrm{result}\:\mathrm{is}\:\mathrm{necessarly}\:\mathrm{among}\:\left\{\left(\mathrm{A}\right),\left(\mathrm{B}\right),\left(\mathrm{C}\right),\left(\mathrm{D}\right),\left(\mathrm{E}\right)\right\}\:\left(\mathrm{2}\right) \\ $$$$\mathrm{well}\:\mathrm{the}\:\mathrm{answere}\:\mathrm{is}\:\left(\mathrm{B}\right) \\ $$$$ \\ $$$${however}\:{I}\:{don}'{t}\:{see}\:{why}\:{these}\:{two}\:{hypothesis}\:{are}\:{true}. \\ $$$${usualy}\:''+…+''\:{refers}\:{to}\:{an}\:{obvious}\:{sequence} \\ $$$${like},\:{for}\:{instance},\:\frac{\mathrm{1}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{6}}+\frac{\mathrm{1}}{\mathrm{24}}+…\:{is}\:\:\frac{\mathrm{1}}{{n}!} \\ $$$${and}\:\frac{\mathrm{1}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{6}}+\frac{\mathrm{1}}{\mathrm{30}}+\frac{\mathrm{1}}{\mathrm{210}}+…=\frac{\mathrm{1}}{\underset{{k}=\mathrm{1}} {\overset{{n}} {\prod}}{p}_{{n}} }\:{where}\:{p}_{{n}} \:{is}\:{the}\:{n}^{{th}} \:{prime}\:{number} \\ $$$$ \\ $$$${in}\:{this}\:{case},\:{I}\:{don}'{t}\:{know}\:{what}\:+…+\:{refers}\:{too}. \\ $$$${so}\:{obviously}\:{my}\:{proof}\:{is}\:{a}\:{bit}\:{lame} \\ $$
Answered by Dwaipayan Shikari last updated on 18/Jun/21
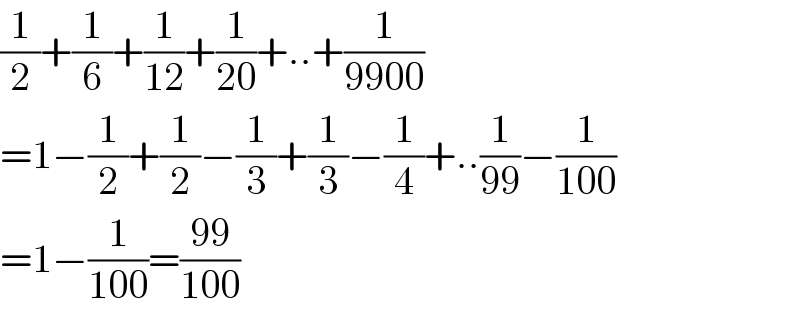
(1/2)+(1/6)+(1/(12))+(1/(20))+..+(1/(9900)) =1−(1/2)+(1/2)−(1/3)+(1/3)−(1/4)+..(1/(99))−(1/(100)) =1−(1/(100))=((99)/(100))
$$\frac{\mathrm{1}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{6}}+\frac{\mathrm{1}}{\mathrm{12}}+\frac{\mathrm{1}}{\mathrm{20}}+..+\frac{\mathrm{1}}{\mathrm{9900}} \\ $$$$=\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{2}}−\frac{\mathrm{1}}{\mathrm{3}}+\frac{\mathrm{1}}{\mathrm{3}}−\frac{\mathrm{1}}{\mathrm{4}}+..\frac{\mathrm{1}}{\mathrm{99}}−\frac{\mathrm{1}}{\mathrm{100}} \\ $$$$=\mathrm{1}−\frac{\mathrm{1}}{\mathrm{100}}=\frac{\mathrm{99}}{\mathrm{100}} \\ $$
Commented by Dwaipayan Shikari last updated on 18/Jun/21
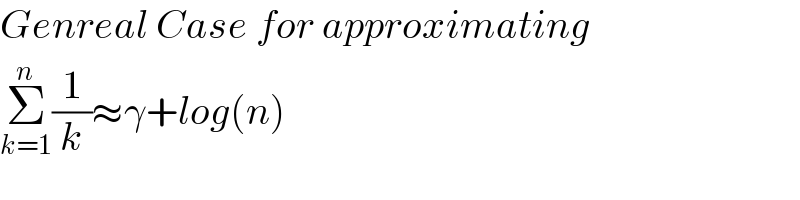
Genreal Case for approximating Σ_(k=1) ^n (1/k)≈γ+log(n)
$${Genreal}\:{Case}\:{for}\:{approximating} \\ $$$$\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}\frac{\mathrm{1}}{{k}}\approx\gamma+{log}\left({n}\right) \\ $$
Answered by MJS_new last updated on 18/Jun/21
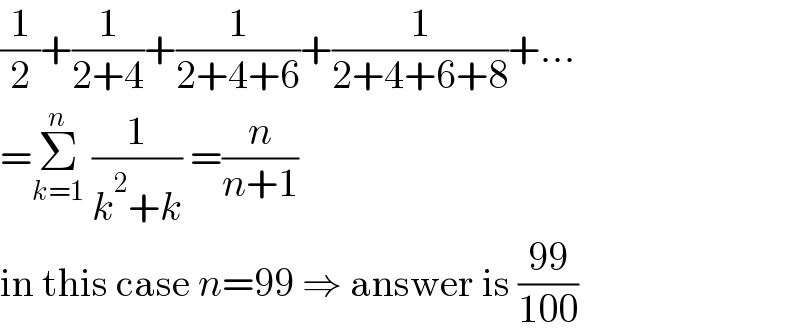
(1/2)+(1/(2+4))+(1/(2+4+6))+(1/(2+4+6+8))+... =Σ_(k=1) ^n (1/(k^2 +k)) =(n/(n+1)) in this case n=99 ⇒ answer is ((99)/(100))
$$\frac{\mathrm{1}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{2}+\mathrm{4}}+\frac{\mathrm{1}}{\mathrm{2}+\mathrm{4}+\mathrm{6}}+\frac{\mathrm{1}}{\mathrm{2}+\mathrm{4}+\mathrm{6}+\mathrm{8}}+… \\ $$$$=\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}\:\frac{\mathrm{1}}{{k}^{\mathrm{2}} +{k}}\:=\frac{{n}}{{n}+\mathrm{1}} \\ $$$$\mathrm{in}\:\mathrm{this}\:\mathrm{case}\:{n}=\mathrm{99}\:\Rightarrow\:\mathrm{answer}\:\mathrm{is}\:\frac{\mathrm{99}}{\mathrm{100}} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *