Question-143808

Question Number 143808 by mnjuly1970 last updated on 18/Jun/21

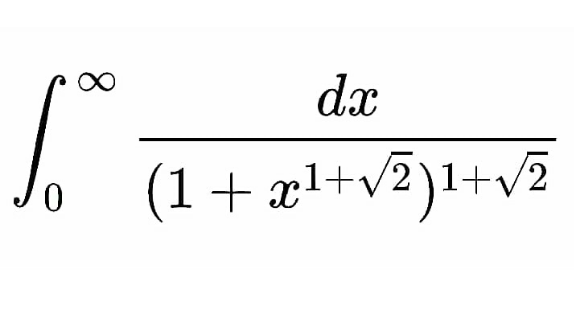
Answered by Dwaipayan Shikari last updated on 18/Jun/21

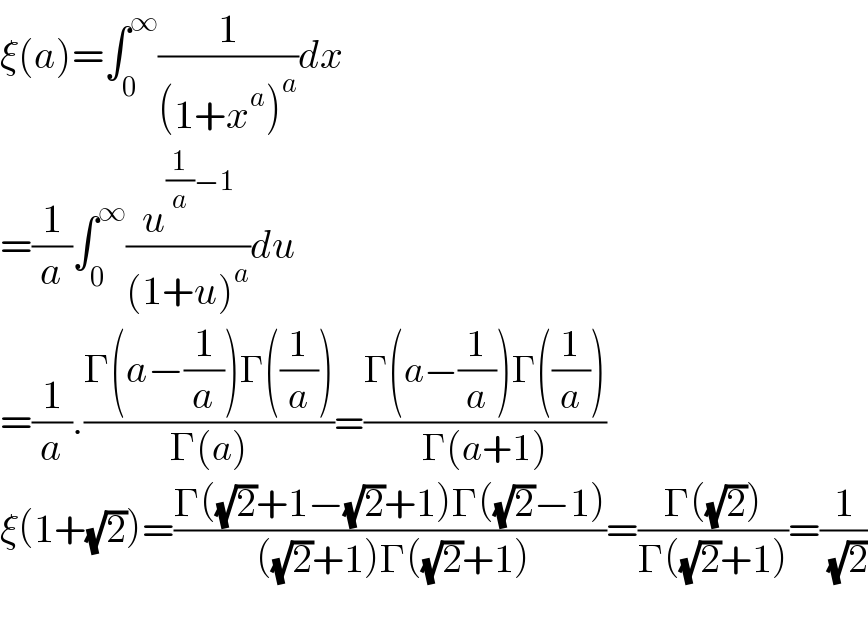
ξ(a)=∫_0 ^∞ (1/((1+x^a )^a ))dx =(1/a)∫_0 ^∞ (u^((1/a)−1) /((1+u)^a ))du =(1/a).((Γ(a−(1/a))Γ((1/a)))/(Γ(a)))=((Γ(a−(1/a))Γ((1/a)))/(Γ(a+1))) ξ(1+(√2))=((Γ((√2)+1−(√2)+1)Γ((√2)−1))/( ((√2)+1)Γ((√2)+1)))=((Γ((√2)))/(Γ((√2)+1)))=(1/( (√2)))

$$\xi\left({a}\right)=\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{1}}{\left(\mathrm{1}+{x}^{{a}} \right)^{{a}} }{dx} \\ $$$$=\frac{\mathrm{1}}{{a}}\int_{\mathrm{0}} ^{\infty} \frac{{u}^{\frac{\mathrm{1}}{{a}}−\mathrm{1}} }{\left(\mathrm{1}+{u}\right)^{{a}} }{du} \\ $$$$=\frac{\mathrm{1}}{{a}}.\frac{\Gamma\left({a}−\frac{\mathrm{1}}{{a}}\right)\Gamma\left(\frac{\mathrm{1}}{{a}}\right)}{\Gamma\left({a}\right)}=\frac{\Gamma\left({a}−\frac{\mathrm{1}}{{a}}\right)\Gamma\left(\frac{\mathrm{1}}{{a}}\right)}{\Gamma\left({a}+\mathrm{1}\right)} \\ $$$$\xi\left(\mathrm{1}+\sqrt{\mathrm{2}}\right)=\frac{\Gamma\left(\sqrt{\mathrm{2}}+\mathrm{1}−\sqrt{\mathrm{2}}+\mathrm{1}\right)\Gamma\left(\sqrt{\mathrm{2}}−\mathrm{1}\right)}{\:\left(\sqrt{\mathrm{2}}+\mathrm{1}\right)\Gamma\left(\sqrt{\mathrm{2}}+\mathrm{1}\right)}=\frac{\Gamma\left(\sqrt{\mathrm{2}}\right)}{\Gamma\left(\sqrt{\mathrm{2}}+\mathrm{1}\right)}=\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}} \\ $$$$ \\ $$

Commented by mnjuly1970 last updated on 18/Jun/21

$$\:\:\:\:\:\:\:{thank}\:{you}\:{so}\:{much}.. \\ $$

Answered by mathmax by abdo last updated on 18/Jun/21

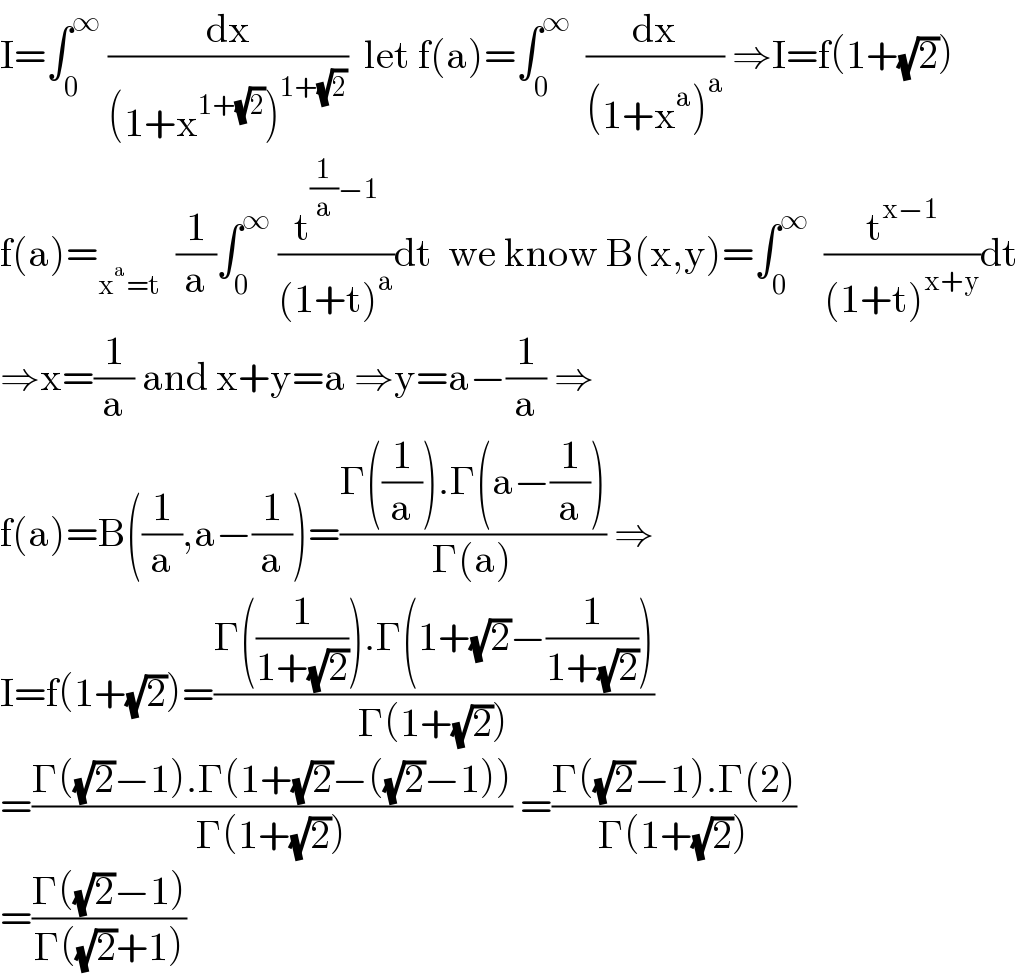
I=∫_0 ^∞ (dx/((1+x^(1+(√2)) )^(1+(√2)) )) let f(a)=∫_0 ^∞ (dx/((1+x^a )^a )) ⇒I=f(1+(√2)) f(a)=_(x^a =t) (1/a)∫_0 ^∞ (t^((1/a)−1) /((1+t)^a ))dt we know B(x,y)=∫_0 ^∞ (t^(x−1) /((1+t)^(x+y) ))dt ⇒x=(1/a) and x+y=a ⇒y=a−(1/a) ⇒ f(a)=B((1/a),a−(1/a))=((Γ((1/a)).Γ(a−(1/a)))/(Γ(a))) ⇒ I=f(1+(√2))=((Γ((1/(1+(√2)))).Γ(1+(√2)−(1/(1+(√2)))))/(Γ(1+(√2)))) =((Γ((√2)−1).Γ(1+(√2)−((√2)−1)))/(Γ(1+(√2)))) =((Γ((√2)−1).Γ(2))/(Γ(1+(√2)))) =((Γ((√2)−1))/(Γ((√2)+1)))

$$\mathrm{I}=\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{dx}}{\left(\mathrm{1}+\mathrm{x}^{\mathrm{1}+\sqrt{\mathrm{2}}} \right)^{\mathrm{1}+\sqrt{\mathrm{2}}} }\:\:\mathrm{let}\:\mathrm{f}\left(\mathrm{a}\right)=\int_{\mathrm{0}} ^{\infty} \:\:\frac{\mathrm{dx}}{\left(\mathrm{1}+\mathrm{x}^{\mathrm{a}} \right)^{\mathrm{a}} }\:\Rightarrow\mathrm{I}=\mathrm{f}\left(\mathrm{1}+\sqrt{\mathrm{2}}\right) \\ $$$$\mathrm{f}\left(\mathrm{a}\right)=_{\mathrm{x}^{\mathrm{a}} =\mathrm{t}} \:\:\frac{\mathrm{1}}{\mathrm{a}}\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{t}^{\frac{\mathrm{1}}{\mathrm{a}}−\mathrm{1}} }{\left(\mathrm{1}+\mathrm{t}\right)^{\mathrm{a}} }\mathrm{dt}\:\:\mathrm{we}\:\mathrm{know}\:\mathrm{B}\left(\mathrm{x},\mathrm{y}\right)=\int_{\mathrm{0}} ^{\infty} \:\:\frac{\mathrm{t}^{\mathrm{x}−\mathrm{1}} }{\left(\mathrm{1}+\mathrm{t}\right)^{\mathrm{x}+\mathrm{y}} }\mathrm{dt} \\ $$$$\Rightarrow\mathrm{x}=\frac{\mathrm{1}}{\mathrm{a}}\:\mathrm{and}\:\mathrm{x}+\mathrm{y}=\mathrm{a}\:\Rightarrow\mathrm{y}=\mathrm{a}−\frac{\mathrm{1}}{\mathrm{a}}\:\Rightarrow \\ $$$$\mathrm{f}\left(\mathrm{a}\right)=\mathrm{B}\left(\frac{\mathrm{1}}{\mathrm{a}},\mathrm{a}−\frac{\mathrm{1}}{\mathrm{a}}\right)=\frac{\Gamma\left(\frac{\mathrm{1}}{\mathrm{a}}\right).\Gamma\left(\mathrm{a}−\frac{\mathrm{1}}{\mathrm{a}}\right)}{\Gamma\left(\mathrm{a}\right)}\:\Rightarrow \\ $$$$\mathrm{I}=\mathrm{f}\left(\mathrm{1}+\sqrt{\mathrm{2}}\right)=\frac{\Gamma\left(\frac{\mathrm{1}}{\mathrm{1}+\sqrt{\mathrm{2}}}\right).\Gamma\left(\mathrm{1}+\sqrt{\mathrm{2}}−\frac{\mathrm{1}}{\mathrm{1}+\sqrt{\mathrm{2}}}\right)}{\Gamma\left(\mathrm{1}+\sqrt{\mathrm{2}}\right)} \\ $$$$=\frac{\Gamma\left(\sqrt{\mathrm{2}}−\mathrm{1}\right).\Gamma\left(\mathrm{1}+\sqrt{\mathrm{2}}−\left(\sqrt{\mathrm{2}}−\mathrm{1}\right)\right)}{\Gamma\left(\mathrm{1}+\sqrt{\mathrm{2}}\right)}\:=\frac{\Gamma\left(\sqrt{\mathrm{2}}−\mathrm{1}\right).\Gamma\left(\mathrm{2}\right)}{\Gamma\left(\mathrm{1}+\sqrt{\mathrm{2}}\right)} \\ $$$$=\frac{\Gamma\left(\sqrt{\mathrm{2}}−\mathrm{1}\right)}{\Gamma\left(\sqrt{\mathrm{2}}+\mathrm{1}\right)} \\ $$

Commented by mathmax by abdo last updated on 18/Jun/21

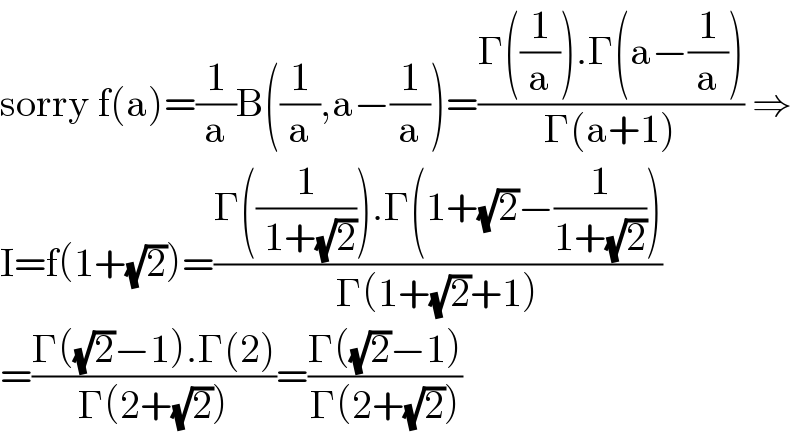
sorry f(a)=(1/a)B((1/a),a−(1/a))=((Γ((1/a)).Γ(a−(1/a)))/(Γ(a+1))) ⇒ I=f(1+(√2))=((Γ((1/( 1+(√2)))).Γ(1+(√2)−(1/(1+(√2)))))/(Γ(1+(√2)+1))) =((Γ((√2)−1).Γ(2))/(Γ(2+(√2))))=((Γ((√2)−1))/(Γ(2+(√2))))

$$\mathrm{sorry}\:\mathrm{f}\left(\mathrm{a}\right)=\frac{\mathrm{1}}{\mathrm{a}}\mathrm{B}\left(\frac{\mathrm{1}}{\mathrm{a}},\mathrm{a}−\frac{\mathrm{1}}{\mathrm{a}}\right)=\frac{\Gamma\left(\frac{\mathrm{1}}{\mathrm{a}}\right).\Gamma\left(\mathrm{a}−\frac{\mathrm{1}}{\mathrm{a}}\right)}{\Gamma\left(\mathrm{a}+\mathrm{1}\right)}\:\Rightarrow \\ $$$$\mathrm{I}=\mathrm{f}\left(\mathrm{1}+\sqrt{\mathrm{2}}\right)=\frac{\Gamma\left(\frac{\mathrm{1}}{\:\mathrm{1}+\sqrt{\mathrm{2}}}\right).\Gamma\left(\mathrm{1}+\sqrt{\mathrm{2}}−\frac{\mathrm{1}}{\mathrm{1}+\sqrt{\mathrm{2}}}\right)}{\Gamma\left(\mathrm{1}+\sqrt{\mathrm{2}}+\mathrm{1}\right)} \\ $$$$=\frac{\Gamma\left(\sqrt{\mathrm{2}}−\mathrm{1}\right).\Gamma\left(\mathrm{2}\right)}{\Gamma\left(\mathrm{2}+\sqrt{\mathrm{2}}\right)}=\frac{\Gamma\left(\sqrt{\mathrm{2}}−\mathrm{1}\right)}{\Gamma\left(\mathrm{2}+\sqrt{\mathrm{2}}\right)} \\ $$

Commented by akolade last updated on 19/Jun/21

$${great}\:{work}\:{sie} \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply