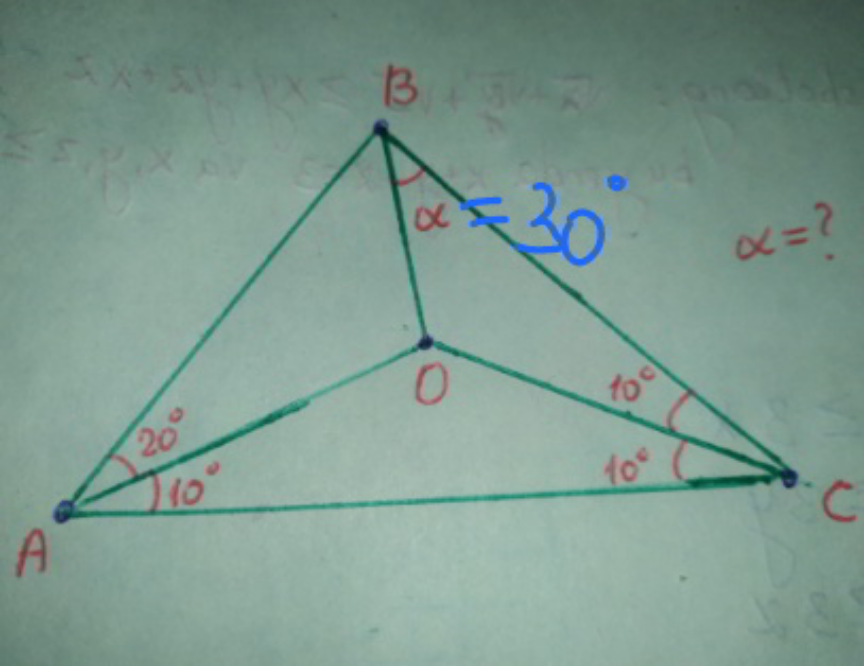
Question Number 143909 by mathdanisur last updated on 19/Jun/21
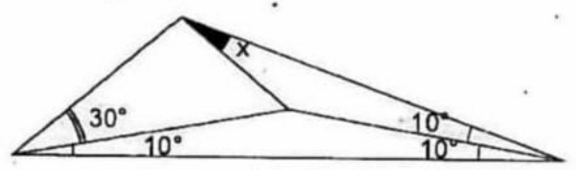
Commented by mr W last updated on 19/Jun/21
$${i}\:{remember}\:{i}\:{solved}\:{the}\:{same} \\ $$$${question}\:{some}\:{days}\:{ago}. \\ $$
Commented by amin96 last updated on 19/Jun/21

$$? \\ $$
Commented by mathdanisur last updated on 19/Jun/21
$${Sir},\:{if}\:{possible}\:{please}\:{take}\:{a}\:{look}\:{at}\:{this} \\ $$
Answered by mr W last updated on 19/Jun/21

Commented by mr W last updated on 19/Jun/21
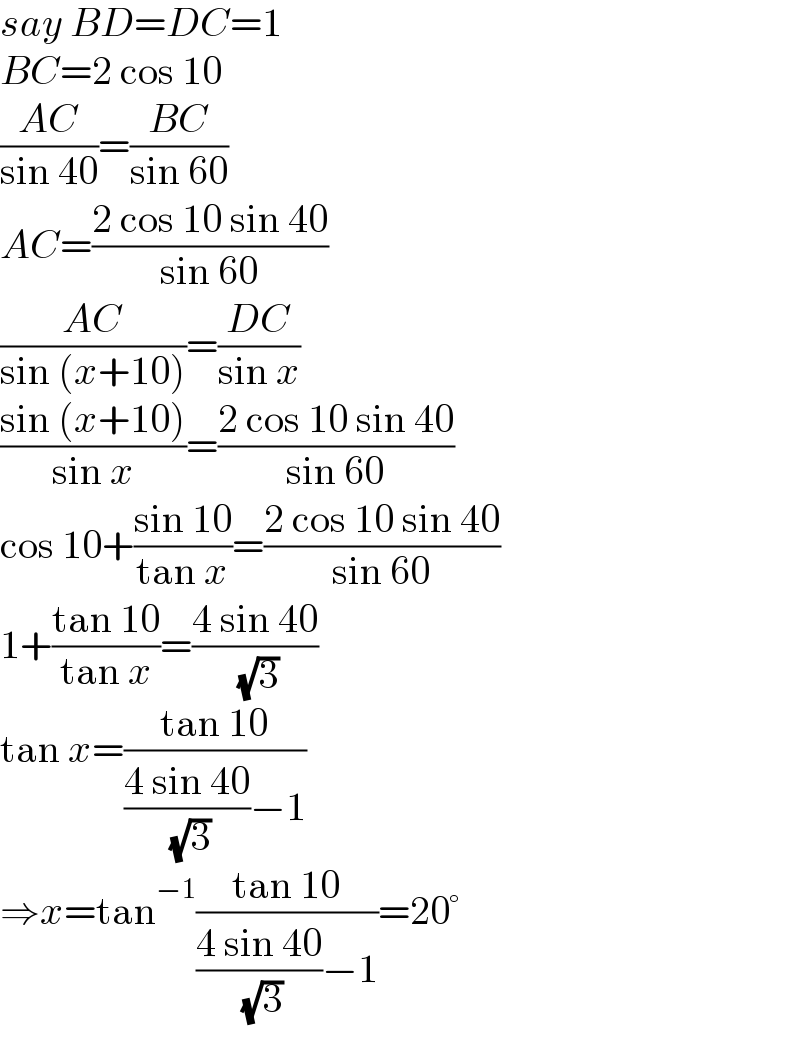
$${say}\:{BD}={DC}=\mathrm{1} \\ $$$${BC}=\mathrm{2}\:\mathrm{cos}\:\mathrm{10} \\ $$$$\frac{{AC}}{\mathrm{sin}\:\mathrm{40}}=\frac{{BC}}{\mathrm{sin}\:\mathrm{60}} \\ $$$${AC}=\frac{\mathrm{2}\:\mathrm{cos}\:\mathrm{10}\:\mathrm{sin}\:\mathrm{40}}{\mathrm{sin}\:\mathrm{60}} \\ $$$$\frac{{AC}}{\mathrm{sin}\:\left({x}+\mathrm{10}\right)}=\frac{{DC}}{\mathrm{sin}\:{x}} \\ $$$$\frac{\mathrm{sin}\:\left({x}+\mathrm{10}\right)}{\mathrm{sin}\:{x}}=\frac{\mathrm{2}\:\mathrm{cos}\:\mathrm{10}\:\mathrm{sin}\:\mathrm{40}}{\mathrm{sin}\:\mathrm{60}} \\ $$$$\mathrm{cos}\:\mathrm{10}+\frac{\mathrm{sin}\:\mathrm{10}}{\mathrm{tan}\:{x}}=\frac{\mathrm{2}\:\mathrm{cos}\:\mathrm{10}\:\mathrm{sin}\:\mathrm{40}}{\mathrm{sin}\:\mathrm{60}} \\ $$$$\mathrm{1}+\frac{\mathrm{tan}\:\mathrm{10}}{\mathrm{tan}\:{x}}=\frac{\mathrm{4}\:\mathrm{sin}\:\mathrm{40}}{\:\sqrt{\mathrm{3}}} \\ $$$$\mathrm{tan}\:{x}=\frac{\mathrm{tan}\:\mathrm{10}}{\frac{\mathrm{4}\:\mathrm{sin}\:\mathrm{40}}{\:\sqrt{\mathrm{3}}}−\mathrm{1}} \\ $$$$\Rightarrow{x}=\mathrm{tan}^{−\mathrm{1}} \frac{\mathrm{tan}\:\mathrm{10}}{\frac{\mathrm{4}\:\mathrm{sin}\:\mathrm{40}}{\:\sqrt{\mathrm{3}}}−\mathrm{1}}=\mathrm{20}° \\ $$
Commented by mathdanisur last updated on 19/Jun/21
$${Yes},\:{perfect},\:{thank}\:{you}\:{dear}\:{sir}.. \\ $$
Answered by mr W last updated on 19/Jun/21
$${similar}\:{question}: \\ $$
Commented by mr W last updated on 19/Jun/21