Question Number 143932 by Ar Brandon last updated on 19/Jun/21

Answered by mathmax by abdo last updated on 19/Jun/21
![1) I=∫_0 ^∞ e^(−t^2 ) dt ⇒I=∫_0 ^a e^(−t^2 ) dt +∫_a ^∞ e^(−t^2 ) dt for alla>0 t→e^(−t^2 ) is continue on[0,a] so integrable ⇒∫_0 ^a e^(−t2) dt<∞ lim_(t→+∞) t^2 e^(−t^2 ) =0 ⇒∫_a ^∞ e^(−t^2 ) <∞ ⇒I is cv.](https://www.tinkutara.com/question/Q143935.png)
$$\left.\mathrm{1}\right)\:\mathrm{I}=\int_{\mathrm{0}} ^{\infty} \mathrm{e}^{−\mathrm{t}^{\mathrm{2}} } \mathrm{dt}\:\:\:\:\:\:\Rightarrow\mathrm{I}=\int_{\mathrm{0}} ^{\mathrm{a}} \:\mathrm{e}^{−\mathrm{t}^{\mathrm{2}} } \mathrm{dt}\:+\int_{\mathrm{a}} ^{\infty} \:\mathrm{e}^{−\mathrm{t}^{\mathrm{2}} } \mathrm{dt}\:\:\:\mathrm{for}\:\mathrm{alla}>\mathrm{0} \\ $$$$\mathrm{t}\rightarrow\mathrm{e}^{−\mathrm{t}^{\mathrm{2}} } \:\mathrm{is}\:\mathrm{continue}\:\mathrm{on}\left[\mathrm{0},\mathrm{a}\right]\:\mathrm{so}\:\mathrm{integrable}\:\:\Rightarrow\int_{\mathrm{0}} ^{\mathrm{a}} \:\mathrm{e}^{−\mathrm{t2}} \mathrm{dt}<\infty \\ $$$$\mathrm{lim}_{\mathrm{t}\rightarrow+\infty} \mathrm{t}^{\mathrm{2}} \mathrm{e}^{−\mathrm{t}^{\mathrm{2}} } =\mathrm{0}\:\Rightarrow\int_{\mathrm{a}} ^{\infty} \:\mathrm{e}^{−\mathrm{t}^{\mathrm{2}} } <\infty\:\Rightarrow\mathrm{I}\:\mathrm{is}\:\mathrm{cv}. \\ $$$$ \\ $$
Answered by mathmax by abdo last updated on 19/Jun/21
![∫_(−1) ^7 (dx/((^3 (√(x+1)))))dx =_(x+1=t^3 ) ∫_0 ^8 ((3t^2 dt)/t)=3∫_0 ^8 tdt=3[(t^2 /2)]_0 ^8 =(3/2)×8^2 ⇒ ths integral is cv.](https://www.tinkutara.com/question/Q143936.png)
$$\left.\int_{−\mathrm{1}} ^{\mathrm{7}} \:\frac{\mathrm{dx}}{\left(^{\mathrm{3}} \sqrt{\mathrm{x}+\mathrm{1}}\right.}\right)\mathrm{dx}\:=_{\mathrm{x}+\mathrm{1}=\mathrm{t}^{\mathrm{3}} } \:\:\:\int_{\mathrm{0}} ^{\mathrm{8}} \:\:\:\frac{\mathrm{3t}^{\mathrm{2}} \mathrm{dt}}{\mathrm{t}}=\mathrm{3}\int_{\mathrm{0}} ^{\mathrm{8}} \:\mathrm{tdt}=\mathrm{3}\left[\frac{\mathrm{t}^{\mathrm{2}} }{\mathrm{2}}\right]_{\mathrm{0}} ^{\mathrm{8}} =\frac{\mathrm{3}}{\mathrm{2}}×\mathrm{8}^{\mathrm{2}} \:\Rightarrow \\ $$$$\mathrm{ths}\:\mathrm{integral}\:\mathrm{is}\:\mathrm{cv}. \\ $$
Answered by mathmax by abdo last updated on 19/Jun/21
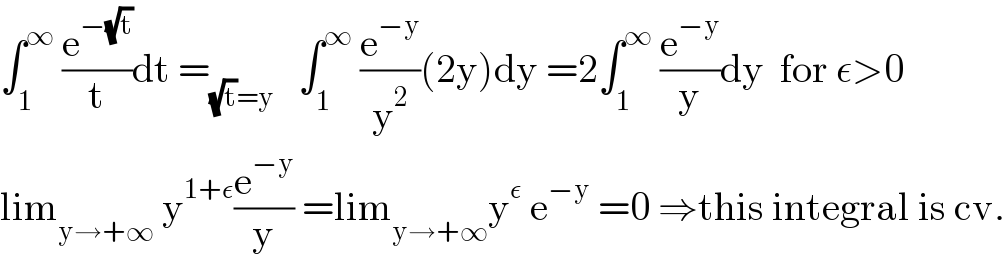
$$\int_{\mathrm{1}} ^{\infty} \:\frac{\mathrm{e}^{−\sqrt{\mathrm{t}}} }{\mathrm{t}}\mathrm{dt}\:=_{\sqrt{\mathrm{t}}=\mathrm{y}} \:\:\:\int_{\mathrm{1}} ^{\infty} \:\frac{\mathrm{e}^{−\mathrm{y}} }{\mathrm{y}^{\mathrm{2}} }\left(\mathrm{2y}\right)\mathrm{dy}\:=\mathrm{2}\int_{\mathrm{1}} ^{\infty} \:\frac{\mathrm{e}^{−\mathrm{y}} }{\mathrm{y}}\mathrm{dy}\:\:\mathrm{for}\:\epsilon>\mathrm{0} \\ $$$$\mathrm{lim}_{\mathrm{y}\rightarrow+\infty} \:\mathrm{y}^{\mathrm{1}+\epsilon} \frac{\mathrm{e}^{−\mathrm{y}} }{\mathrm{y}}\:=\mathrm{lim}_{\mathrm{y}\rightarrow+\infty} \mathrm{y}^{\epsilon} \:\mathrm{e}^{−\mathrm{y}} \:=\mathrm{0}\:\Rightarrow\mathrm{this}\:\mathrm{integral}\:\mathrm{is}\:\mathrm{cv}. \\ $$
Answered by mathmax by abdo last updated on 19/Jun/21
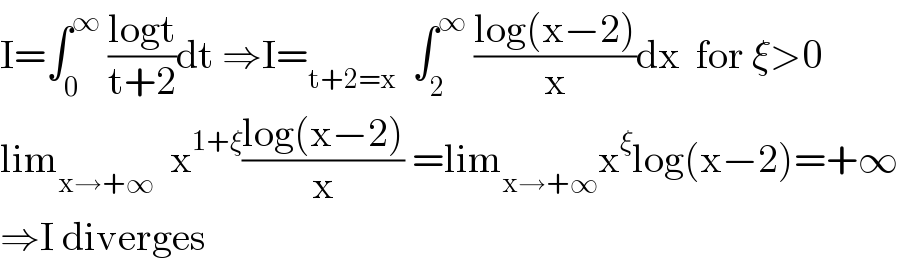
$$\mathrm{I}=\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{logt}}{\mathrm{t}+\mathrm{2}}\mathrm{dt}\:\Rightarrow\mathrm{I}=_{\mathrm{t}+\mathrm{2}=\mathrm{x}} \:\:\int_{\mathrm{2}} ^{\infty} \:\frac{\mathrm{log}\left(\mathrm{x}−\mathrm{2}\right)}{\mathrm{x}}\mathrm{dx}\:\:\mathrm{for}\:\xi>\mathrm{0} \\ $$$$\mathrm{lim}_{\mathrm{x}\rightarrow+\infty} \:\:\mathrm{x}^{\mathrm{1}+\xi} \frac{\mathrm{log}\left(\mathrm{x}−\mathrm{2}\right)}{\mathrm{x}}\:=\mathrm{lim}_{\mathrm{x}\rightarrow+\infty} \mathrm{x}^{\xi} \mathrm{log}\left(\mathrm{x}−\mathrm{2}\right)=+\infty \\ $$$$\Rightarrow\mathrm{I}\:\mathrm{diverges} \\ $$
