Question Number 143979 by mathdanisur last updated on 20/Jun/21

Answered by mitica last updated on 20/Jun/21
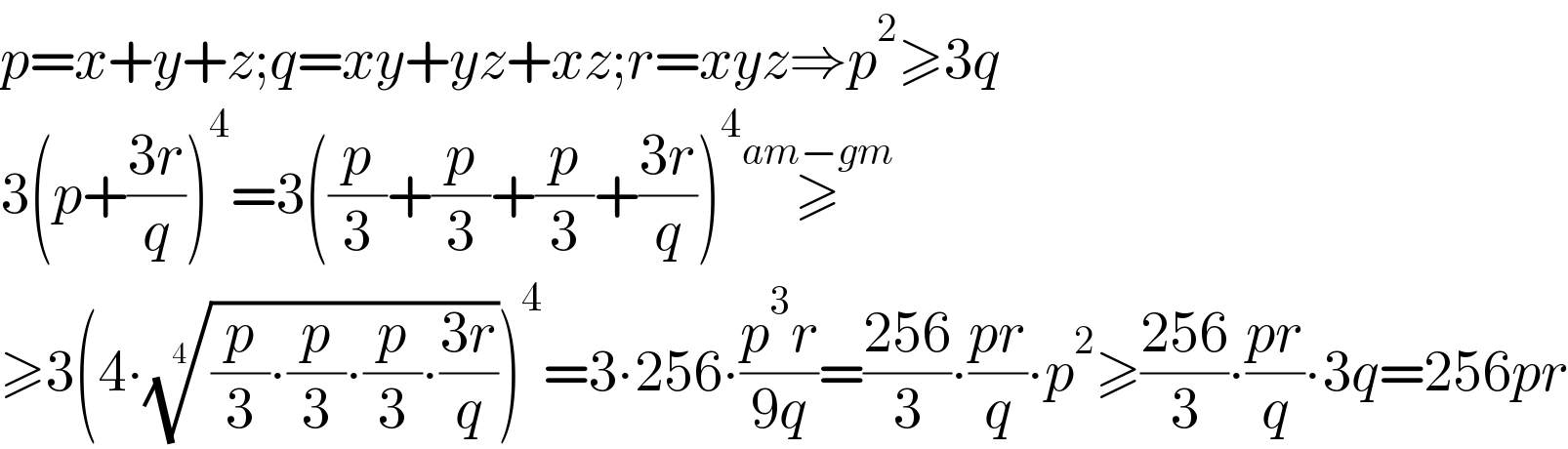
$${p}={x}+{y}+{z};{q}={xy}+{yz}+{xz};{r}={xyz}\Rightarrow{p}^{\mathrm{2}} \geqslant\mathrm{3}{q} \\ $$$$\mathrm{3}\left({p}+\frac{\mathrm{3}{r}}{{q}}\right)^{\mathrm{4}} =\mathrm{3}\left(\frac{{p}}{\mathrm{3}}+\frac{{p}}{\mathrm{3}}+\frac{{p}}{\mathrm{3}}+\frac{\mathrm{3}{r}}{{q}}\right)^{\mathrm{4}} \overset{{am}−{gm}} {\geqslant} \\ $$$$\geqslant\mathrm{3}\left(\mathrm{4}\centerdot\sqrt[{\mathrm{4}}]{\frac{{p}}{\mathrm{3}}\centerdot\frac{{p}}{\mathrm{3}}\centerdot\frac{{p}}{\mathrm{3}}\centerdot\frac{\mathrm{3}{r}}{{q}}}\right)^{\mathrm{4}} =\mathrm{3}\centerdot\mathrm{256}\centerdot\frac{{p}^{\mathrm{3}} {r}}{\mathrm{9}{q}}=\frac{\mathrm{256}}{\mathrm{3}}\centerdot\frac{{pr}}{{q}}\centerdot{p}^{\mathrm{2}} \geqslant\frac{\mathrm{256}}{\mathrm{3}}\centerdot\frac{{pr}}{{q}}\centerdot\mathrm{3}{q}=\mathrm{256}{pr} \\ $$
Commented by justtry last updated on 20/Jun/21

$${it}'{s}\:{great}..{i}\:{to}\:{understanding},\:{maybe}\:{you}\:{want}\:{write}\:\frac{\mathrm{256}}{\mathrm{3}\:}.\frac{{pr}}{{q}}.{p}^{\mathrm{2}} \left({but}\:{is}\:{writen}\:{q}^{\mathrm{2}} \right) \\ $$
Commented by mitica last updated on 20/Jun/21

$${p}^{\mathrm{2}} \: \\ $$$$ \\ $$
Commented by mathdanisur last updated on 20/Jun/21
$${thnks}\:{sir},\:{alot}\:{cool} \\ $$
