Question Number 143980 by mathdanisur last updated on 20/Jun/21

Answered by mitica last updated on 20/Jun/21
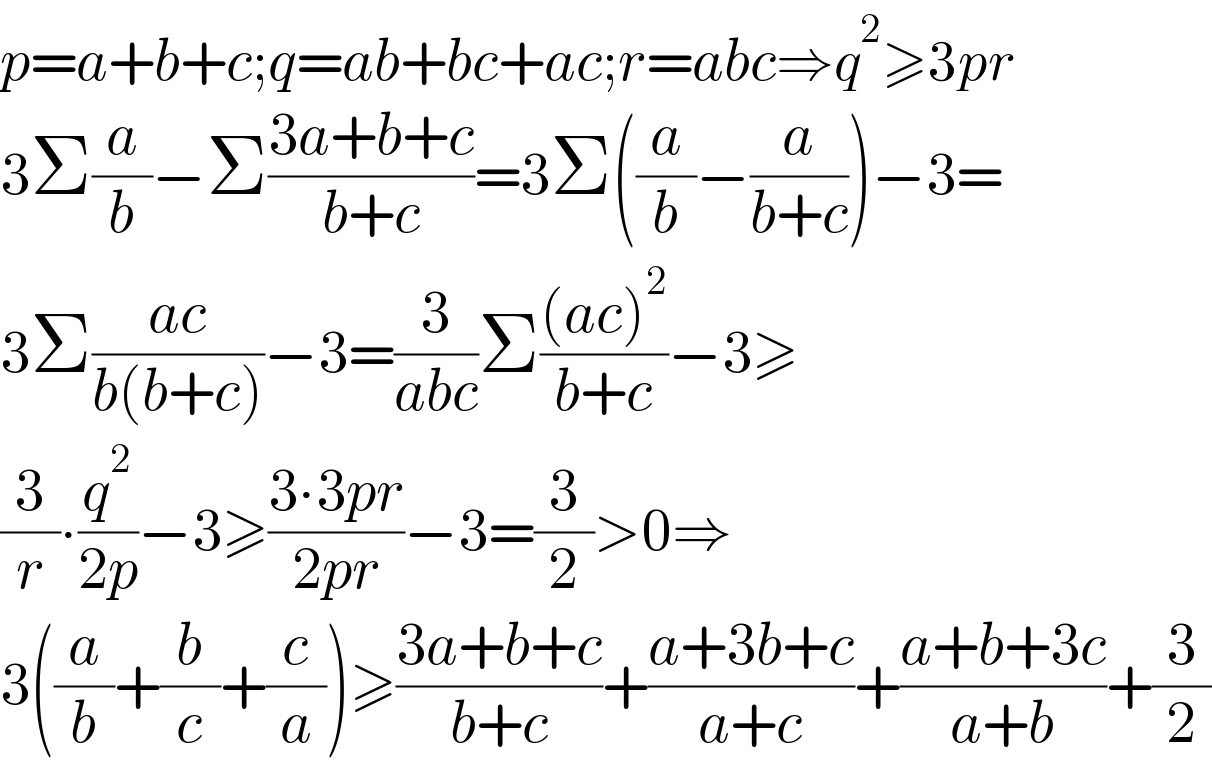
$${p}={a}+{b}+{c};{q}={ab}+{bc}+{ac};{r}={abc}\Rightarrow{q}^{\mathrm{2}} \geqslant\mathrm{3}{pr} \\ $$$$\mathrm{3}\Sigma\frac{{a}}{{b}}−\Sigma\frac{\mathrm{3}{a}+{b}+{c}}{{b}+{c}}=\mathrm{3}\Sigma\left(\frac{{a}}{{b}}−\frac{{a}}{{b}+{c}}\right)−\mathrm{3}= \\ $$$$\mathrm{3}\Sigma\frac{{ac}}{{b}\left({b}+{c}\right)}−\mathrm{3}=\frac{\mathrm{3}}{{abc}}\Sigma\frac{\left({ac}\right)^{\mathrm{2}} }{{b}+{c}}−\mathrm{3}\geqslant \\ $$$$\frac{\mathrm{3}}{{r}}\centerdot\frac{{q}^{\mathrm{2}} }{\mathrm{2}{p}}−\mathrm{3}\geqslant\frac{\mathrm{3}\centerdot\mathrm{3}{pr}}{\mathrm{2}{pr}}−\mathrm{3}=\frac{\mathrm{3}}{\mathrm{2}}>\mathrm{0}\Rightarrow \\ $$$$\mathrm{3}\left(\frac{{a}}{{b}}+\frac{{b}}{{c}}+\frac{{c}}{{a}}\right)\geqslant\frac{\mathrm{3}{a}+{b}+{c}}{{b}+{c}}+\frac{{a}+\mathrm{3}{b}+{c}}{{a}+{c}}+\frac{{a}+{b}+\mathrm{3}{c}}{{a}+{b}}+\frac{\mathrm{3}}{\mathrm{2}} \\ $$
Commented by mathdanisur last updated on 20/Jun/21

$${Cool}\:{sir}\:{thanks}\:{but}\:{p},{q},{r}\:{what}\:{it}\:{means}? \\ $$
