Menu Close

Question-144042

Tinku Tara 0 Comments
Pin




Question Number 144042 by maryxxxx last updated on 20/Jun/21
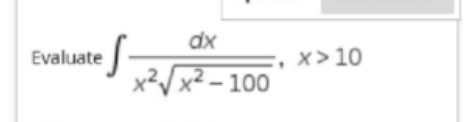
Answered by mindispower last updated on 20/Jun/21
∫(dx/(x^3 (√(1−(((10)/x))^2 )))) y=((100)/x^2 ),y<1⇒dy=((−200)/x^3 )dx ⇒((−1)/(200))∫(dy/( (√(1−y))))dy=(1/(100))(√(1−y))+c=((√(1−((100)/x^2 )))/(100))+c
$$\int\frac{{dx}}{{x}^{\mathrm{3}} \sqrt{\mathrm{1}−\left(\frac{\mathrm{10}}{{x}}\right)^{\mathrm{2}} }} \\ $$$${y}=\frac{\mathrm{100}}{{x}^{\mathrm{2}} },{y}<\mathrm{1}\Rightarrow{dy}=\frac{−\mathrm{200}}{{x}^{\mathrm{3}} }{dx} \\ $$$$\Rightarrow\frac{−\mathrm{1}}{\mathrm{200}}\int\frac{{dy}}{\:\sqrt{\mathrm{1}−{y}}}{dy}=\frac{\mathrm{1}}{\mathrm{100}}\sqrt{\mathrm{1}−{y}}+{c}=\frac{\sqrt{\mathrm{1}−\frac{\mathrm{100}}{{x}^{\mathrm{2}} }}}{\mathrm{100}}+{c} \\ $$$$ \\ $$$$ \\ $$
Answered by liberty last updated on 21/Jun/21
I=∫ (dx/(x^3 (√(1−100x^(−2) )))) let u=(√(1−100x^(−2) )) ∧ u^2 =1−100x^(−2) ⇒2u du = 200x^(−3) dx ; (dx/x^3 ) = ((u du)/(100)) I= ∫ (1/u)(((u du)/(100))) = (u/(100)) + c = ((√(1−100x^(−2) ))/(100)) + c = ((√(x−100))/(100x)) + c
$$\mathrm{I}=\int\:\frac{\mathrm{dx}}{\mathrm{x}^{\mathrm{3}} \:\sqrt{\mathrm{1}−\mathrm{100x}^{−\mathrm{2}} }} \\ $$$$\mathrm{let}\:\mathrm{u}=\sqrt{\mathrm{1}−\mathrm{100x}^{−\mathrm{2}} }\:\wedge\:\mathrm{u}^{\mathrm{2}} =\mathrm{1}−\mathrm{100x}^{−\mathrm{2}} \\ $$$$\Rightarrow\mathrm{2u}\:\mathrm{du}\:=\:\mathrm{200x}^{−\mathrm{3}} \:\mathrm{dx}\:;\:\frac{\mathrm{dx}}{\mathrm{x}^{\mathrm{3}} }\:=\:\frac{\mathrm{u}\:\mathrm{du}}{\mathrm{100}} \\ $$$$\mathrm{I}=\:\int\:\frac{\mathrm{1}}{\mathrm{u}}\left(\frac{\mathrm{u}\:\mathrm{du}}{\mathrm{100}}\right)\:=\:\frac{\mathrm{u}}{\mathrm{100}}\:+\:\mathrm{c}\: \\ $$$$\:\:=\:\frac{\sqrt{\mathrm{1}−\mathrm{100x}^{−\mathrm{2}} }}{\mathrm{100}}\:+\:\mathrm{c}\: \\ $$$$\:\:=\:\frac{\sqrt{\mathrm{x}−\mathrm{100}}}{\mathrm{100x}}\:+\:\mathrm{c}\: \\ $$
Answered by mathmax by abdo last updated on 21/Jun/21
Ψ=∫ (dx/(x^2 (√(x^2 −100)))) ⇒Ψ=_(x=10cht) ∫ ((10sht dt)/(100ch^2 t×10sht)) =(1/(100))∫ (dt/(ch^2 t)) =(1/(50))∫ (dt/(ch(2t)+1)) =_(2t=u) (1/(50))∫ (du/(2(chu +1))) =(1/(100))∫ (du/(((e^u +e^(−u) )/2)+1))=(1/(50))∫ (du/(e^u +e^(−u) +2)) =_(e^u =z) (1/(50))∫ (dz/(z(z+z^(−1) +2)))=(1/(50))∫ (dz/(z^2 +2z+1)) =(1/(50))∫ (dz/((z+1)^2 )) =−(1/(50(z+1))) +K =−(1/(50(e^u +1)))+K=−(1/(50(1+e^(t/2) )))+K t=argch((x/(10)))=log((x/(10))+(√((x^2 /(100))−1))) ⇒ Ψ=−(1/(50(1+e^((1/2)log((x/(10))+(√((x^2 /(100))−1)))) )) +K =−(1/(50(1+(√((x/(10))+(√((x^2 /(100))−1)))))))+K (x>10)
$$\Psi=\int\:\frac{\mathrm{dx}}{\mathrm{x}^{\mathrm{2}} \sqrt{\mathrm{x}^{\mathrm{2}} −\mathrm{100}}}\:\Rightarrow\Psi=_{\mathrm{x}=\mathrm{10cht}} \:\:\int\:\:\frac{\mathrm{10sht}\:\mathrm{dt}}{\mathrm{100ch}^{\mathrm{2}} \mathrm{t}×\mathrm{10sht}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{100}}\int\:\:\frac{\mathrm{dt}}{\mathrm{ch}^{\mathrm{2}} \mathrm{t}}\:=\frac{\mathrm{1}}{\mathrm{50}}\int\:\:\frac{\mathrm{dt}}{\mathrm{ch}\left(\mathrm{2t}\right)+\mathrm{1}}\:=_{\mathrm{2t}=\mathrm{u}} \:\:\:\frac{\mathrm{1}}{\mathrm{50}}\int\:\:\frac{\mathrm{du}}{\mathrm{2}\left(\mathrm{chu}\:+\mathrm{1}\right)} \\ $$$$=\frac{\mathrm{1}}{\mathrm{100}}\int\:\:\frac{\mathrm{du}}{\frac{\mathrm{e}^{\mathrm{u}} +\mathrm{e}^{−\mathrm{u}} }{\mathrm{2}}+\mathrm{1}}=\frac{\mathrm{1}}{\mathrm{50}}\int\:\:\:\:\frac{\mathrm{du}}{\mathrm{e}^{\mathrm{u}} +\mathrm{e}^{−\mathrm{u}} \:+\mathrm{2}} \\ $$$$=_{\mathrm{e}^{\mathrm{u}} \:=\mathrm{z}} \:\:\:\frac{\mathrm{1}}{\mathrm{50}}\int\:\:\:\frac{\mathrm{dz}}{\mathrm{z}\left(\mathrm{z}+\mathrm{z}^{−\mathrm{1}} +\mathrm{2}\right)}=\frac{\mathrm{1}}{\mathrm{50}}\int\:\:\frac{\mathrm{dz}}{\mathrm{z}^{\mathrm{2}} \:+\mathrm{2z}+\mathrm{1}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{50}}\int\:\:\frac{\mathrm{dz}}{\left(\mathrm{z}+\mathrm{1}\right)^{\mathrm{2}} }\:=−\frac{\mathrm{1}}{\mathrm{50}\left(\mathrm{z}+\mathrm{1}\right)}\:+\mathrm{K} \\ $$$$=−\frac{\mathrm{1}}{\mathrm{50}\left(\mathrm{e}^{\mathrm{u}} \:+\mathrm{1}\right)}+\mathrm{K}=−\frac{\mathrm{1}}{\mathrm{50}\left(\mathrm{1}+\mathrm{e}^{\frac{\mathrm{t}}{\mathrm{2}}} \right)}+\mathrm{K} \\ $$$$\mathrm{t}=\mathrm{argch}\left(\frac{\mathrm{x}}{\mathrm{10}}\right)=\mathrm{log}\left(\frac{\mathrm{x}}{\mathrm{10}}+\sqrt{\frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{100}}−\mathrm{1}}\right)\:\Rightarrow \\ $$$$\Psi=−\frac{\mathrm{1}}{\mathrm{50}\left(\mathrm{1}+\mathrm{e}^{\frac{\mathrm{1}}{\mathrm{2}}\mathrm{log}\left(\frac{\mathrm{x}}{\mathrm{10}}+\sqrt{\frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{100}}−\mathrm{1}}\right)} \right.}\:+\mathrm{K} \\ $$$$=−\frac{\mathrm{1}}{\mathrm{50}\left(\mathrm{1}+\sqrt{\left.\frac{\mathrm{x}}{\mathrm{10}}+\sqrt{\frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{100}}−\mathrm{1}}\right)}\right.}+\mathrm{K}\:\:\:\:\left(\mathrm{x}>\mathrm{10}\right) \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *