Question Number 1468 by havandip last updated on 11/Aug/15

$$ \\ $$
Answered by 123456 last updated on 11/Aug/15
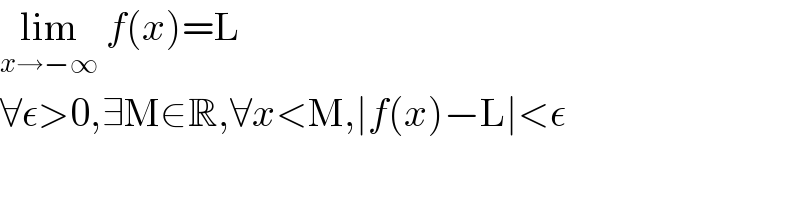
$$\underset{{x}\rightarrow−\infty} {\mathrm{lim}}\:{f}\left({x}\right)=\mathrm{L} \\ $$$$\forall\epsilon>\mathrm{0},\exists\mathrm{M}\in\mathbb{R},\forall{x}<\mathrm{M},\mid{f}\left({x}\right)−\mathrm{L}\mid<\epsilon \\ $$
Commented by 123456 last updated on 11/Aug/15

$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{{a}^{{x}} −\mathrm{1}}{{x}}=\mathrm{ln}\:{a} \\ $$
Commented by 123456 last updated on 11/Aug/15
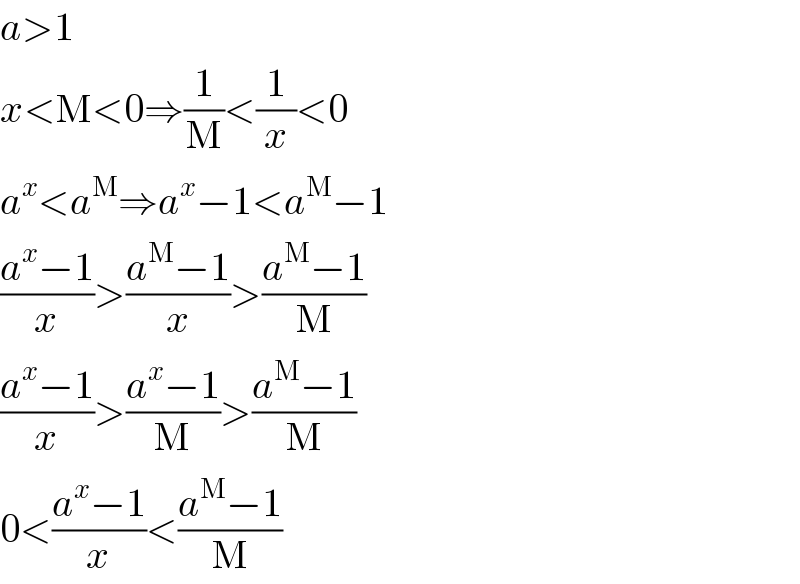
$${a}>\mathrm{1} \\ $$$${x}<\mathrm{M}<\mathrm{0}\Rightarrow\frac{\mathrm{1}}{\mathrm{M}}<\frac{\mathrm{1}}{{x}}<\mathrm{0} \\ $$$${a}^{{x}} <{a}^{\mathrm{M}} \Rightarrow{a}^{{x}} −\mathrm{1}<{a}^{\mathrm{M}} −\mathrm{1} \\ $$$$\frac{{a}^{{x}} −\mathrm{1}}{{x}}>\frac{{a}^{\mathrm{M}} −\mathrm{1}}{{x}}>\frac{{a}^{\mathrm{M}} −\mathrm{1}}{\mathrm{M}} \\ $$$$\frac{{a}^{{x}} −\mathrm{1}}{{x}}>\frac{{a}^{{x}} −\mathrm{1}}{\mathrm{M}}>\frac{{a}^{\mathrm{M}} −\mathrm{1}}{\mathrm{M}} \\ $$$$\mathrm{0}<\frac{{a}^{{x}} −\mathrm{1}}{{x}}<\frac{{a}^{\mathrm{M}} −\mathrm{1}}{\mathrm{M}} \\ $$
