Question Number 1763 by Gerlândio Almeida last updated on 18/Sep/15

$$ \\ $$
Commented by 123456 last updated on 18/Sep/15
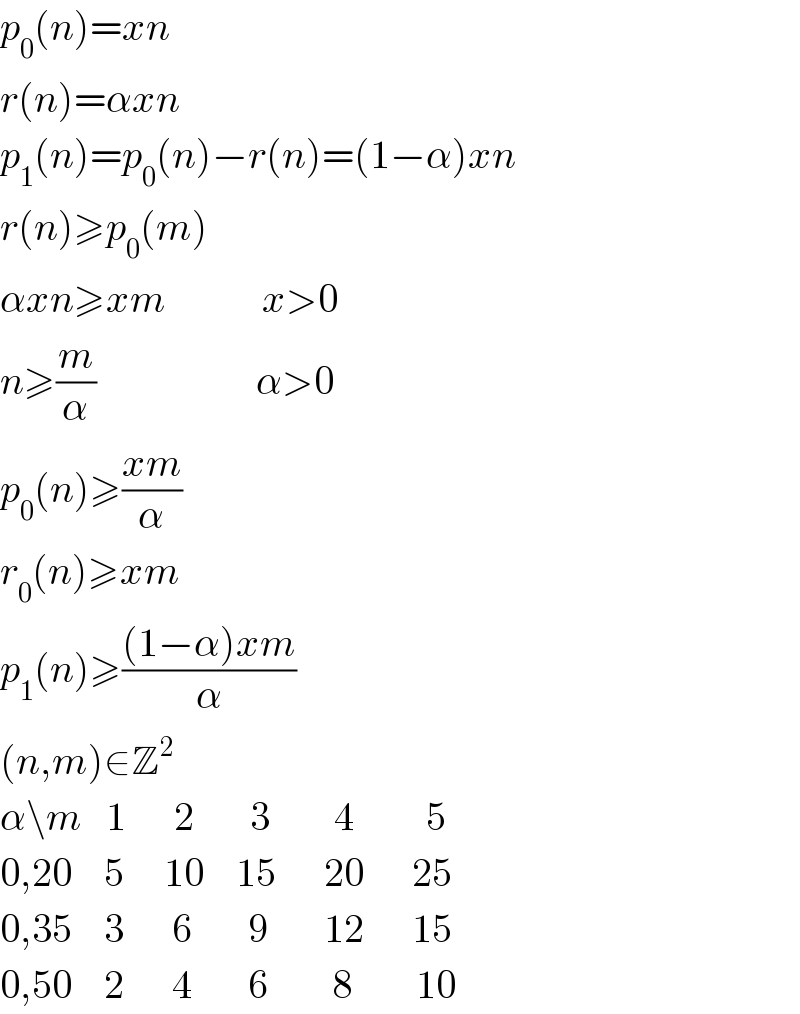
$${p}_{\mathrm{0}} \left({n}\right)={xn} \\ $$$${r}\left({n}\right)=\alpha{xn} \\ $$$${p}_{\mathrm{1}} \left({n}\right)={p}_{\mathrm{0}} \left({n}\right)−{r}\left({n}\right)=\left(\mathrm{1}−\alpha\right){xn} \\ $$$${r}\left({n}\right)\geqslant{p}_{\mathrm{0}} \left({m}\right) \\ $$$$\alpha{xn}\geqslant{xm}\:\:\:\:\:\:\:\:\:\:\:\:{x}>\mathrm{0} \\ $$$${n}\geqslant\frac{{m}}{\alpha}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\alpha>\mathrm{0} \\ $$$${p}_{\mathrm{0}} \left({n}\right)\geqslant\frac{{xm}}{\alpha} \\ $$$${r}_{\mathrm{0}} \left({n}\right)\geqslant{xm} \\ $$$${p}_{\mathrm{1}} \left({n}\right)\geqslant\frac{\left(\mathrm{1}−\alpha\right){xm}}{\alpha} \\ $$$$\left({n},{m}\right)\in\mathbb{Z}^{\mathrm{2}} \\ $$$$\alpha\backslash{m}\:\:\:\mathrm{1}\:\:\:\:\:\:\mathrm{2}\:\:\:\:\:\:\:\mathrm{3}\:\:\:\:\:\:\:\:\mathrm{4}\:\:\:\:\:\:\:\:\:\mathrm{5} \\ $$$$\mathrm{0},\mathrm{20}\:\:\:\:\mathrm{5}\:\:\:\:\:\mathrm{10}\:\:\:\:\mathrm{15}\:\:\:\:\:\:\mathrm{20}\:\:\:\:\:\:\mathrm{25} \\ $$$$\mathrm{0},\mathrm{35}\:\:\:\:\mathrm{3}\:\:\:\:\:\:\mathrm{6}\:\:\:\:\:\:\:\mathrm{9}\:\:\:\:\:\:\:\mathrm{12}\:\:\:\:\:\:\mathrm{15} \\ $$$$\mathrm{0},\mathrm{50}\:\:\:\:\mathrm{2}\:\:\:\:\:\:\mathrm{4}\:\:\:\:\:\:\:\mathrm{6}\:\:\:\:\:\:\:\:\mathrm{8}\:\:\:\:\:\:\:\:\mathrm{10} \\ $$
Answered by 123456 last updated on 18/Sep/15
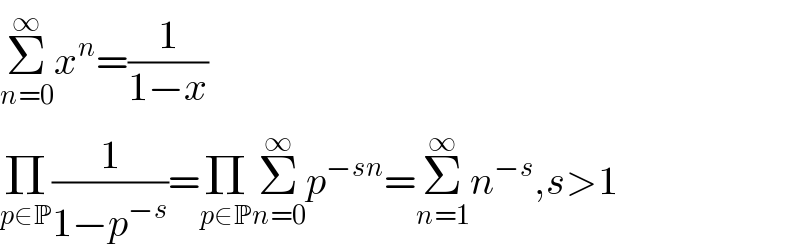
$$\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}{x}^{{n}} =\frac{\mathrm{1}}{\mathrm{1}−{x}} \\ $$$$\underset{{p}\in\mathbb{P}} {\prod}\frac{\mathrm{1}}{\mathrm{1}−{p}^{−{s}} }=\underset{{p}\in\mathbb{P}} {\prod}\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}{p}^{−{sn}} =\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}{n}^{−{s}} ,{s}>\mathrm{1} \\ $$
