Question-4164

Question Number 4164 by Yozzii last updated on 30/Dec/15

Commented by Yozzii last updated on 30/Dec/15

$${Can}\:{anyone}\:{provide}\:{a}\:{well}\:{explained} \\ $$$${proof}\:{of}\:{this}\:{formula}?\:{I}\:{don}'{t} \\ $$$${understand}\:{why}\:{it}\:{works}. \\ $$

Commented by prakash jain last updated on 30/Dec/15

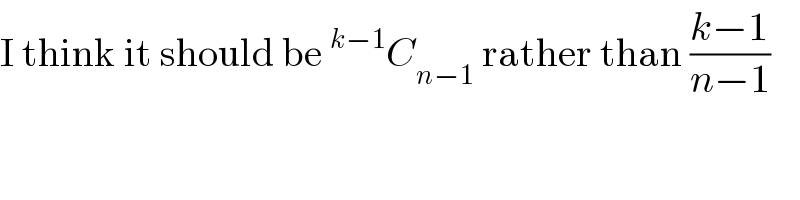
I think it should be^(k−1) C_(n−1) rather than ((k−1)/(n−1))

$$\mathrm{I}\:\mathrm{think}\:\mathrm{it}\:\mathrm{should}\:\mathrm{be}\:^{{k}−\mathrm{1}} {C}_{{n}−\mathrm{1}} \:\mathrm{rather}\:\mathrm{than}\:\frac{{k}−\mathrm{1}}{{n}−\mathrm{1}} \\ $$

Answered by prakash jain last updated on 31/Dec/15

★★★★....★ Say a total of k stars are k−balls. To divide these into n−parts you need n−1 bars to be placed in a total of k−1 position. Number of ways to achieve^(k−1) C_(n−1) Example 6 stars and 4 boxes. ★★★★★★ ★∣★★∣★★∣★ (1,2,2,1) ★∣★∣★∣★★★ (1,1,1,3) To divide 6 stars among four boxes you can 3 bars in 5 spaces between stars. Since no box is empty max one bar can be placed between 2 stars.

$$\bigstar\bigstar\bigstar\bigstar….\bigstar \\ $$$$\mathrm{Say}\:\mathrm{a}\:\mathrm{total}\:\mathrm{of}\:{k}\:\mathrm{stars}\:\mathrm{are}\:{k}−{balls}. \\ $$$$\mathrm{To}\:\mathrm{divide}\:\mathrm{these}\:\mathrm{into}\:{n}−\mathrm{parts}\:\mathrm{you}\:\mathrm{need} \\ $$$${n}−\mathrm{1}\:\mathrm{bars}\:\mathrm{to}\:\mathrm{be}\:\mathrm{placed}\:\mathrm{in}\:\mathrm{a}\:\mathrm{total}\:\mathrm{of}\:{k}−\mathrm{1} \\ $$$$\mathrm{position}. \\ $$$$\mathrm{Number}\:\mathrm{of}\:\mathrm{ways}\:\mathrm{to}\:\mathrm{achieve}\:^{{k}−\mathrm{1}} {C}_{{n}−\mathrm{1}} \\ $$$$\mathrm{Example}\:\mathrm{6}\:\mathrm{stars}\:\mathrm{and}\:\mathrm{4}\:\mathrm{boxes}. \\ $$$$\bigstar\bigstar\bigstar\bigstar\bigstar\bigstar \\ $$$$\bigstar\mid\bigstar\bigstar\mid\bigstar\bigstar\mid\bigstar\:\:\left(\mathrm{1},\mathrm{2},\mathrm{2},\mathrm{1}\right) \\ $$$$\bigstar\mid\bigstar\mid\bigstar\mid\bigstar\bigstar\bigstar\:\:\left(\mathrm{1},\mathrm{1},\mathrm{1},\mathrm{3}\right) \\ $$$$\mathrm{To}\:\mathrm{divide}\:\mathrm{6}\:\mathrm{stars}\:\mathrm{among}\:\mathrm{four}\:\mathrm{boxes}\:\mathrm{you} \\ $$$$\mathrm{can}\:\mathrm{3}\:\mathrm{bars}\:\mathrm{in}\:\mathrm{5}\:\mathrm{spaces}\:\mathrm{between}\:\mathrm{stars}. \\ $$$$\mathrm{Since}\:\mathrm{no}\:\mathrm{box}\:\mathrm{is}\:\mathrm{empty}\:\mathrm{max}\:\mathrm{one}\:\mathrm{bar}\:\mathrm{can} \\ $$$$\mathrm{be}\:\mathrm{placed}\:\mathrm{between}\:\mathrm{2}\:\mathrm{stars}. \\ $$

Commented by Yozzii last updated on 30/Dec/15

$${Thanks}\:{a}\:{lot}\:{for}\:{the}\:{help}! \\ $$

Commented by Rasheed Soomro last updated on 31/Dec/15

$$\mathcal{EASY}\:\mathcal{E}{xplanation}! \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply