Question Number 4166 by Filup last updated on 30/Dec/15
Commented by prakash jain last updated on 31/Dec/15
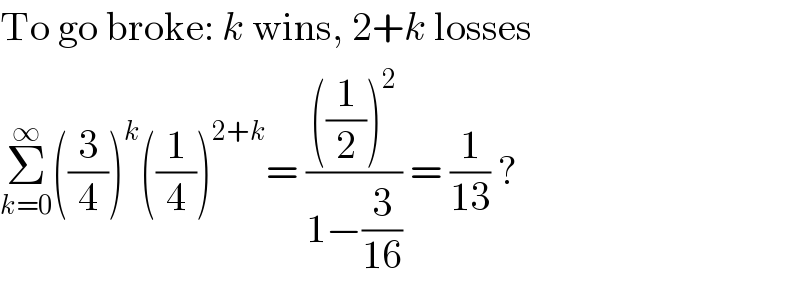
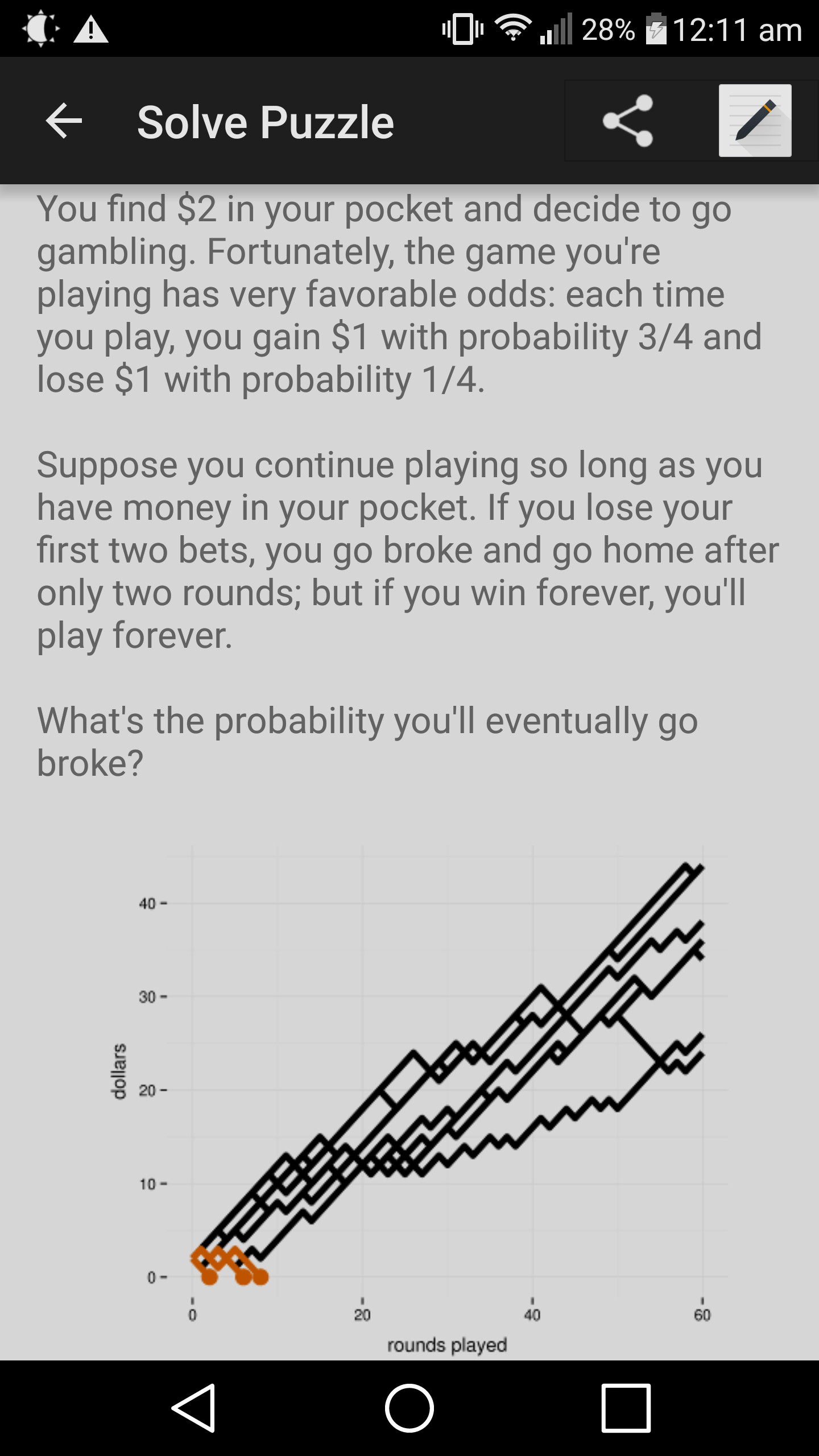
$$\mathrm{To}\:\mathrm{go}\:\mathrm{broke}:\:{k}\:\mathrm{wins},\:\mathrm{2}+{k}\:\mathrm{losses} \\ $$$$\underset{{k}=\mathrm{0}} {\overset{\infty} {\sum}}\left(\frac{\mathrm{3}}{\mathrm{4}}\right)^{{k}} \left(\frac{\mathrm{1}}{\mathrm{4}}\right)^{\mathrm{2}+{k}} =\:\frac{\left(\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} }{\mathrm{1}−\frac{\mathrm{3}}{\mathrm{16}}}\:=\:\frac{\mathrm{1}}{\mathrm{13}}\:? \\ $$
Commented by Filup last updated on 31/Dec/15
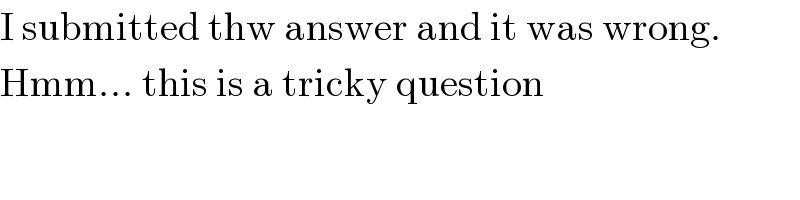
$$\mathrm{I}\:\mathrm{submitted}\:\mathrm{thw}\:\mathrm{answer}\:\mathrm{and}\:\mathrm{it}\:\mathrm{was}\:\mathrm{wrong}. \\ $$$$\mathrm{Hmm}…\:\mathrm{this}\:\mathrm{is}\:\mathrm{a}\:\mathrm{tricky}\:\mathrm{question} \\ $$
Commented by Filup last updated on 31/Dec/15
Commented by prakash jain last updated on 31/Dec/15
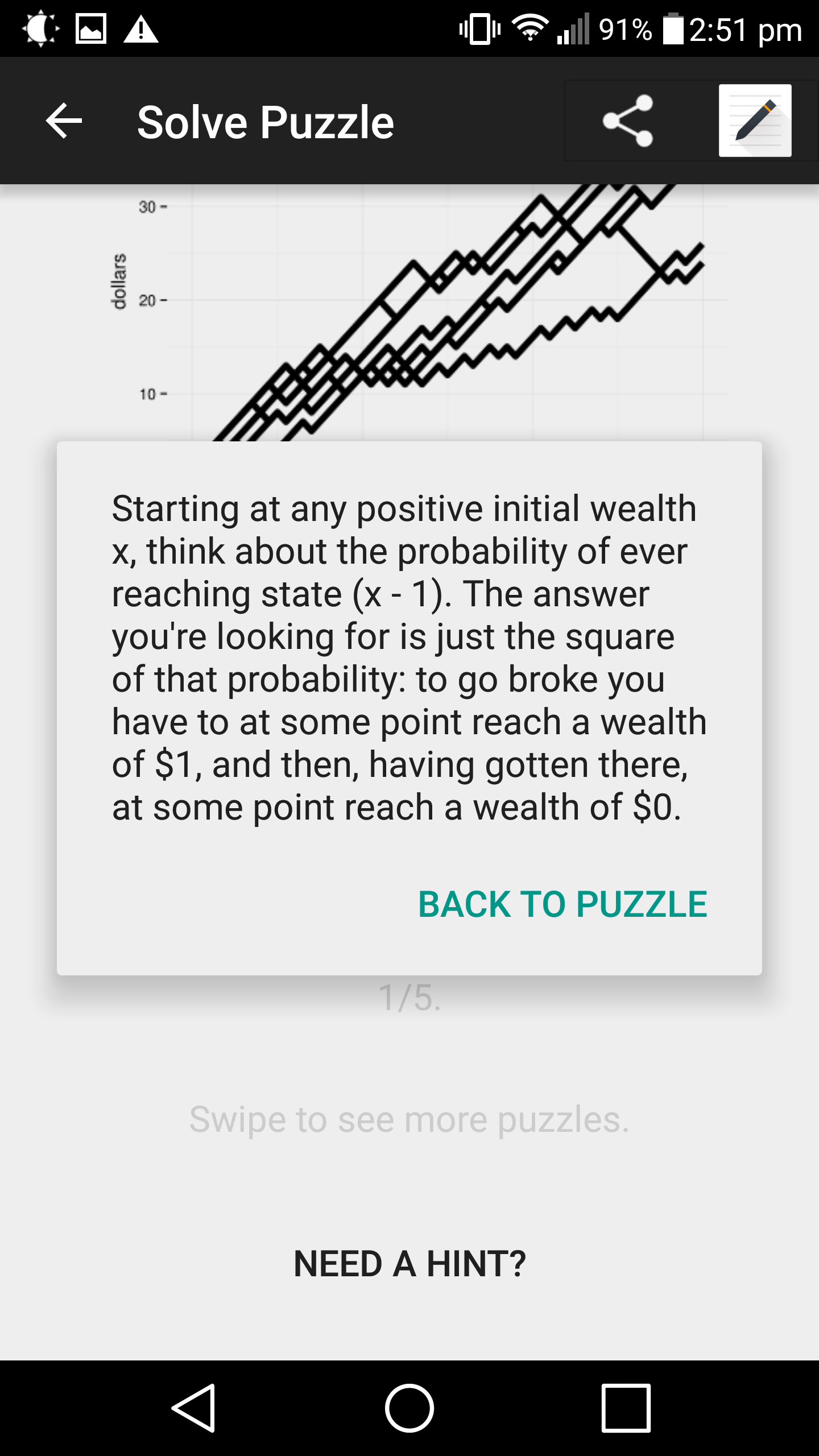
$$\mathrm{What}\:\mathrm{is}\:\mathrm{the}\:\mathrm{correct}\:\mathrm{answer}? \\ $$
Commented by Yozzii last updated on 31/Dec/15
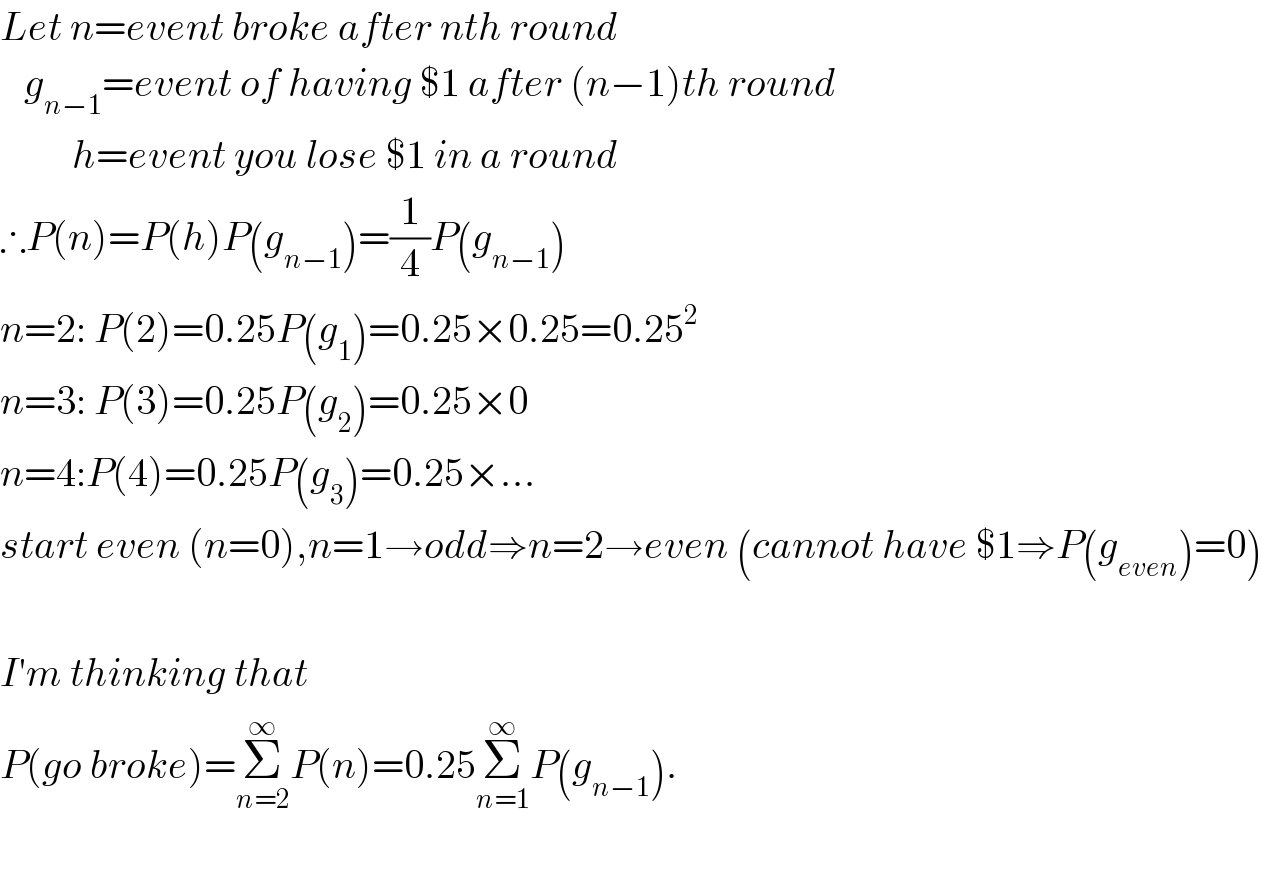
$${Let}\:{n}={event}\:{broke}\:{after}\:{nth}\:{round} \\ $$$$\:\:\:{g}_{{n}−\mathrm{1}} ={event}\:{of}\:{having}\:\$\mathrm{1}\:{after}\:\left({n}−\mathrm{1}\right){th}\:{round} \\ $$$$\:\:\:\:\:\:\:\:\:{h}={event}\:{you}\:{lose}\:\$\mathrm{1}\:{in}\:{a}\:{round} \\ $$$$\therefore{P}\left({n}\right)={P}\left({h}\right){P}\left({g}_{{n}−\mathrm{1}} \right)=\frac{\mathrm{1}}{\mathrm{4}}{P}\left({g}_{{n}−\mathrm{1}} \right) \\ $$$${n}=\mathrm{2}:\:{P}\left(\mathrm{2}\right)=\mathrm{0}.\mathrm{25}{P}\left({g}_{\mathrm{1}} \right)=\mathrm{0}.\mathrm{25}×\mathrm{0}.\mathrm{25}=\mathrm{0}.\mathrm{25}^{\mathrm{2}} \\ $$$${n}=\mathrm{3}:\:{P}\left(\mathrm{3}\right)=\mathrm{0}.\mathrm{25}{P}\left({g}_{\mathrm{2}} \right)=\mathrm{0}.\mathrm{25}×\mathrm{0} \\ $$$${n}=\mathrm{4}:{P}\left(\mathrm{4}\right)=\mathrm{0}.\mathrm{25}{P}\left({g}_{\mathrm{3}} \right)=\mathrm{0}.\mathrm{25}×… \\ $$$${start}\:{even}\:\left({n}=\mathrm{0}\right),{n}=\mathrm{1}\rightarrow{odd}\Rightarrow{n}=\mathrm{2}\rightarrow{even}\:\left({cannot}\:{have}\:\$\mathrm{1}\Rightarrow{P}\left({g}_{{even}} \right)=\mathrm{0}\right) \\ $$$$ \\ $$$${I}'{m}\:{thinking}\:{that} \\ $$$${P}\left({go}\:{broke}\right)=\underset{{n}=\mathrm{2}} {\overset{\infty} {\sum}}{P}\left({n}\right)=\mathrm{0}.\mathrm{25}\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}{P}\left({g}_{{n}−\mathrm{1}} \right). \\ $$$$ \\ $$
Commented by Yozzii last updated on 31/Dec/15
Commented by Yozzii last updated on 31/Dec/15

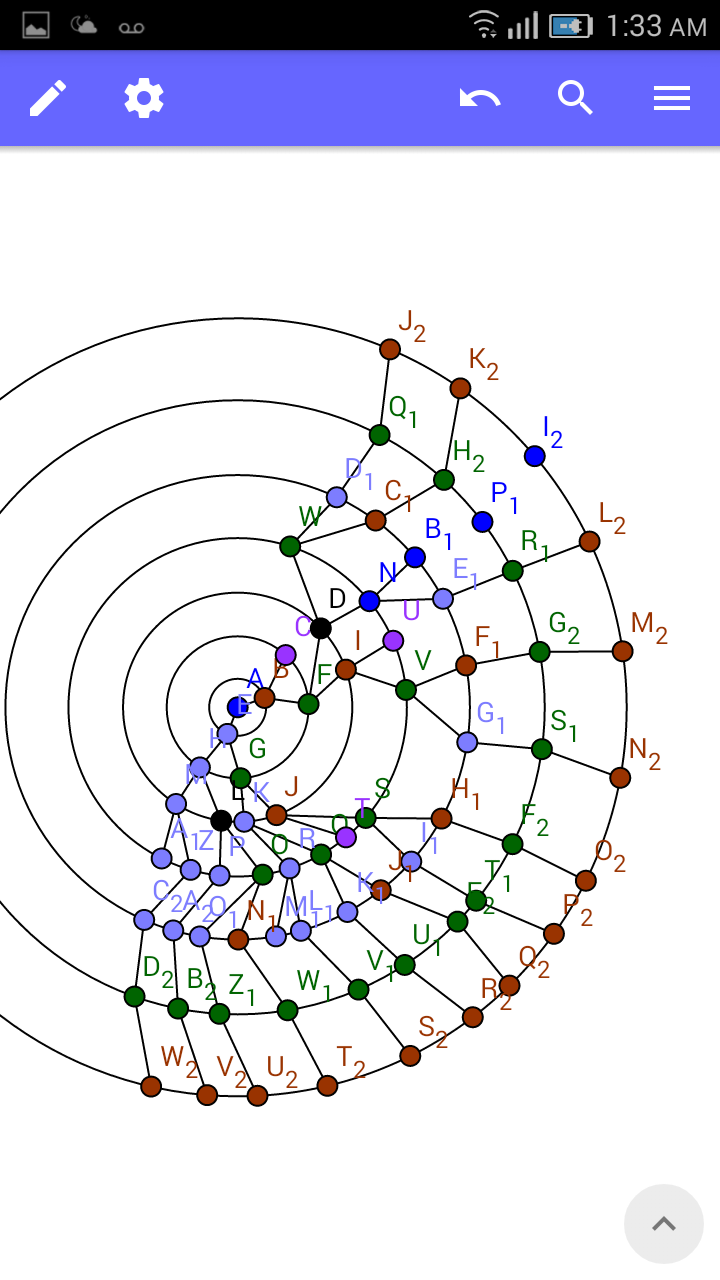
$${I}'{ve}\:{created}\:{a}\:{crazy}\:'{event}\:{sequence}' \\ $$$${diagram}.\:{The}\:{red}\:{points}\:{represent} \\ $$$${having}\:\$\mathrm{1}\:{after}\:{the}\:{nth}\:{round}, \\ $$$${where}\:{the}\:{nth}\:{round}\:{is}\:{given}\:{by} \\ $$$${the}\:{nth}\:{circle}\:\:{Green}\:{dots}\:{represent} \\ $$$$\$\mathrm{2}.\:{Deep}\:{purple}\:{dots}\:{represent}\: \\ $$$${termination}\:{of}\:{a}\:{game}. \\ $$$${All}\:{remaining}\:{dots}\:{could}\:{be}\:\$\mathrm{3}\:{or} \\ $$$$\$\mathrm{4},{etc}…{Following}\:{the}\:{colour}\:{coding}\:{helps} \\ $$$${to}\:{think}\:{of}\:{what}\:{could}\:{possibly}\: \\ $$$${lead}\:{to}\:\$\mathrm{2}\:{for}\:{example}.\:{I}'{m}\:{only} \\ $$$${concerned}\:{with}\:{counting}\:{resulting}\:{red}\:{dots}. \\ $$$$ \\ $$$${So},\:{for}\:{n}=\mathrm{1}:\:{you}\:{can}\:{get}\:\$\mathrm{1}\:{in}\:\mathrm{1}\:{way} \\ $$$${for}\:{n}=\mathrm{3},\:{you}\:{get}\:\$\mathrm{1}\:{in}\:\mathrm{2}\:{ways} \\ $$$${for}\:{n}=\mathrm{5}\:{you}\:{get}\:\$\mathrm{1}\:{in}\:\mathrm{5}\:{ways} \\ $$$${for}\:{n}=\mathrm{7},\:{you}\:{get}\:\$\mathrm{1}\:{in}\:\mathrm{14}\:{ways} \\ $$$$ \\ $$$${Let}\:{a}\left({n}\right)={number}\:{of}\:{ways}\:{of}\:{getting} \\ $$$$\$\mathrm{1}\:{after}\:\left(\mathrm{2}{n}−\mathrm{1}\right){th}\:{round}. \\ $$$$\Rightarrow{a}\left(\mathrm{1}\right)=\mathrm{1},{a}\left(\mathrm{2}\right)=\mathrm{2},{a}\left(\mathrm{3}\right)=\mathrm{5},{a}\left(\mathrm{4}\right)=\mathrm{14} \\ $$$${a}\left(\mathrm{2}\right)−{a}\left(\mathrm{1}\right)=\mathrm{2}−\mathrm{1}=\mathrm{1}=\mathrm{3}^{\mathrm{0}} \\ $$$${a}\left(\mathrm{3}\right)−{a}\left(\mathrm{2}\right)=\mathrm{5}−\mathrm{2}=\mathrm{3}^{\mathrm{1}} \\ $$$${a}\left(\mathrm{4}\right)−{a}\left(\mathrm{3}\right)=\mathrm{14}−\mathrm{5}=\mathrm{9}=\mathrm{3}^{\mathrm{2}} \\ $$$${a}\left({n}+\mathrm{1}\right)−{a}\left({n}\right)=\mathrm{3}^{{n}−\mathrm{1}} \:?\:\: \\ $$$$ \\ $$$${These}\:{are}\:{important}\:{in}\:{finding} \\ $$$${the}\:{multiples}\:{for}\:{each}\:{event}\: \\ $$$${probability}\:\left({getting}\:\$\mathrm{1}\:{on}\:{the}\:{nth}\:{round}\right). \\ $$
Commented by prakash jain last updated on 31/Dec/15

$$\mathrm{Mistake}\:\mathrm{in}\:\mathrm{my}\:\mathrm{previous}\:\mathrm{argument}: \\ $$$${k}=\mathrm{0}:\:\left(\frac{\mathrm{1}}{\mathrm{4}}\right)^{\mathrm{2}} \\ $$$${k}=\mathrm{1}:\:\left(\frac{\mathrm{3}}{\mathrm{4}}\right)\left(\frac{\mathrm{1}}{\mathrm{4}}\right)^{\mathrm{3}} +\left(\frac{\mathrm{1}}{\mathrm{4}}\right)^{\mathrm{2}} \left(\frac{\mathrm{3}}{\mathrm{4}}\right)\left(\frac{\mathrm{1}}{\mathrm{4}}\right)=\mathrm{2}\left(\frac{\mathrm{3}}{\mathrm{4}}\right)\left(\frac{\mathrm{1}}{\mathrm{4}}\right)^{\mathrm{3}} \\ $$$${k}=\mathrm{2}:\:^{\mathrm{2}{k}} {C}_{{k}} \:\left(\frac{\mathrm{3}}{\mathrm{4}}\right)^{{k}} \left(\frac{\mathrm{1}}{\mathrm{4}}\right)^{{k}+\mathrm{2}} \\ $$$${k}\:\mathrm{wins}\:\mathrm{can}\:\mathrm{occur}\:^{\mathrm{2}{k}} {C}_{{k}} \:\mathrm{different}\:\mathrm{ways}. \\ $$$${P}=\underset{{k}=\mathrm{0}} {\overset{\infty} {\sum}}\:^{\mathrm{2}{k}} {C}_{{k}} \left(\frac{\mathrm{3}}{\mathrm{4}}\right)^{{k}} \left(\frac{\mathrm{1}}{\mathrm{4}}\right)^{{k}+\mathrm{2}} \\ $$$$\mathrm{Treating}\:\mathrm{one}\:\mathrm{dollar}\:\mathrm{loss}\:\mathrm{is}\:\mathrm{easier}: \\ $$
Commented by prakash jain last updated on 31/Dec/15
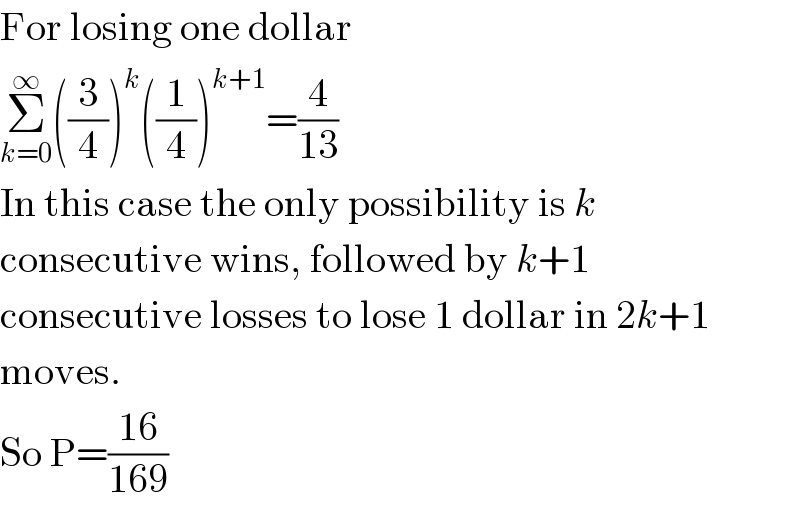
$$\mathrm{For}\:\mathrm{losing}\:\mathrm{one}\:\mathrm{dollar} \\ $$$$\underset{{k}=\mathrm{0}} {\overset{\infty} {\sum}}\left(\frac{\mathrm{3}}{\mathrm{4}}\right)^{{k}} \left(\frac{\mathrm{1}}{\mathrm{4}}\right)^{{k}+\mathrm{1}} =\frac{\mathrm{4}}{\mathrm{13}} \\ $$$$\mathrm{In}\:\mathrm{this}\:\mathrm{case}\:\mathrm{the}\:\mathrm{only}\:\mathrm{possibility}\:\mathrm{is}\:{k} \\ $$$$\mathrm{consecutive}\:\mathrm{wins},\:\mathrm{followed}\:\mathrm{by}\:{k}+\mathrm{1} \\ $$$$\mathrm{consecutive}\:\mathrm{losses}\:\mathrm{to}\:\mathrm{lose}\:\mathrm{1}\:\mathrm{dollar}\:\mathrm{in}\:\mathrm{2}{k}+\mathrm{1} \\ $$$$\mathrm{moves}. \\ $$$$\mathrm{So}\:\mathrm{P}=\frac{\mathrm{16}}{\mathrm{169}} \\ $$
