Question Number 4420 by ankitbhawarkar333gmail.com last updated on 24/Jan/16

Answered by Yozzii last updated on 24/Jan/16
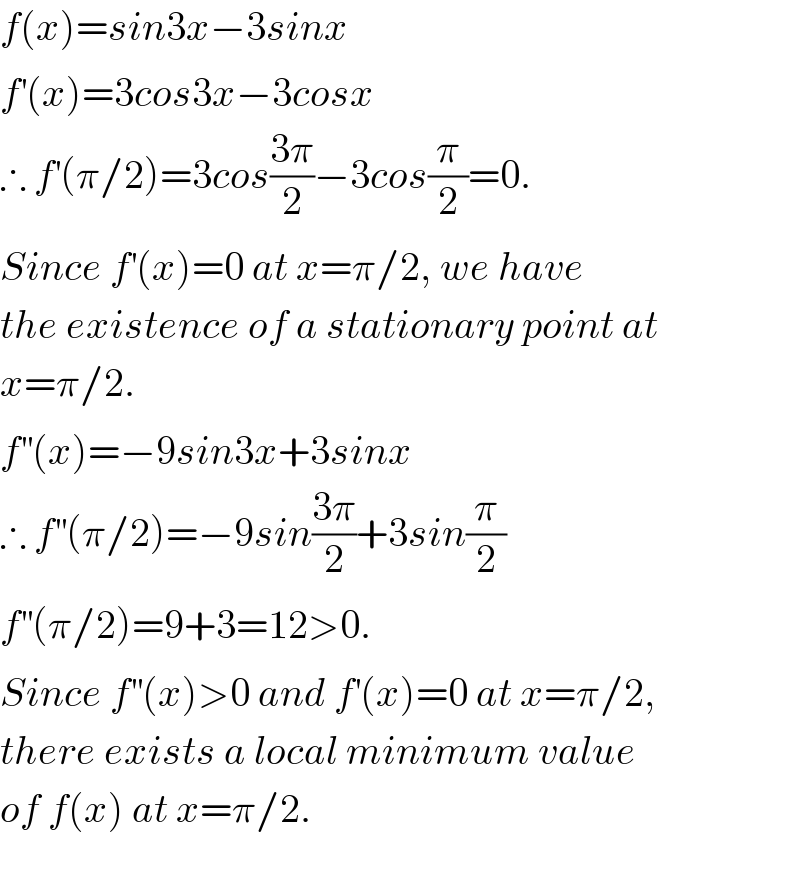
$${f}\left({x}\right)={sin}\mathrm{3}{x}−\mathrm{3}{sinx} \\ $$$${f}^{'} \left({x}\right)=\mathrm{3}{cos}\mathrm{3}{x}−\mathrm{3}{cosx} \\ $$$$\therefore\:{f}^{'} \left(\pi/\mathrm{2}\right)=\mathrm{3}{cos}\frac{\mathrm{3}\pi}{\mathrm{2}}−\mathrm{3}{cos}\frac{\pi}{\mathrm{2}}=\mathrm{0}. \\ $$$${Since}\:{f}^{'} \left({x}\right)=\mathrm{0}\:{at}\:{x}=\pi/\mathrm{2},\:{we}\:{have} \\ $$$${the}\:{existence}\:{of}\:{a}\:{stationary}\:{point}\:{at} \\ $$$${x}=\pi/\mathrm{2}. \\ $$$${f}^{''} \left({x}\right)=−\mathrm{9}{sin}\mathrm{3}{x}+\mathrm{3}{sinx} \\ $$$$\therefore\:{f}^{''} \left(\pi/\mathrm{2}\right)=−\mathrm{9}{sin}\frac{\mathrm{3}\pi}{\mathrm{2}}+\mathrm{3}{sin}\frac{\pi}{\mathrm{2}} \\ $$$${f}^{''} \left(\pi/\mathrm{2}\right)=\mathrm{9}+\mathrm{3}=\mathrm{12}>\mathrm{0}. \\ $$$${Since}\:{f}^{''} \left({x}\right)>\mathrm{0}\:{and}\:{f}^{'} \left({x}\right)=\mathrm{0}\:{at}\:{x}=\pi/\mathrm{2}, \\ $$$${there}\:{exists}\:{a}\:{local}\:{minimum}\:{value} \\ $$$${of}\:{f}\left({x}\right)\:{at}\:{x}=\pi/\mathrm{2}. \\ $$$$ \\ $$
