Menu Close

Question-4505

Tinku Tara 0 Comments
Pin




Question Number 4505 by Yozzii last updated on 03/Feb/16
Commented by Yozzii last updated on 03/Feb/16
△ACD and △DBE are equilateral. F is the midpoint of AE and G is the midpoint of BC. D is a point on the line AB. Prove that △FGD is equilateral. (The diagram is only a guide.)
$$\bigtriangleup{ACD}\:{and}\:\bigtriangleup{DBE}\:{are}\:{equilateral}. \\ $$$${F}\:{is}\:{the}\:{midpoint}\:{of}\:{AE}\:{and}\:{G}\:{is}\:{the} \\ $$$${midpoint}\:{of}\:{BC}.\:{D}\:{is}\:{a}\:{point}\:{on}\:{the} \\ $$$${line}\:{AB}.\:{Prove}\:{that}\:\bigtriangleup{FGD}\:{is}\: \\ $$$${equilateral}.\: \\ $$$$\left({The}\:{diagram}\:{is}\:{only}\:{a}\:{guide}.\right) \\ $$
Answered by Rasheed Soomro last updated on 05/Feb/16
^• Let common vertex of triangles D=(0,0) and AD and DB are along x-axis. (AD and DB are collinear) ^• Let each side of △ADC=a units and each side of △BDE=b units ^• Let A is on left side of D and B is on right side of D So A=(−a,0) and B=(b,0) It can be shown easily that C=(−(a/2),((√3)/2)a) and E=((b/2),((√3)/2)b) G is midpoint of BC So G=( (1/2)(−(a/2)+b),(1/2)(((√3)/2)a+0) )=(((2b−a)/4),(((√3)a)/4)) F is midpoint of AE So F=((1/2)(−a+(b/2)),(1/2)(((√3)/2)b+0))=(((b−2a)/4),(((√3) b)/4)) Now in △FGD FG=(√((((2b−a)/4)−((b−2a)/4))^2 +((((√3)a)/4)−(((√3) b)/4))^2 )) =(√((((b+a)^2 )/(16))+((3( a−b)^2 )/(16))))= =((√(a^2 +2ab+b^2 +3a^2 −6ab+3b^2 ))/4) =((√(4a^2 −4ab+4b^2 ))/4)=(1/2)(√(a^2 −ab+b^2 )) FD=(√((((b−2a)/4)−0)^2 +((((√3) b)/4)−0)^2 )) =(√((b^2 −4ab+4a^2 +3b^2 )/(16)))=(1/2)(√(a^2 −ab+b^2 )) GD=(√((((2b−a)/4)−0)^2 +((((√3)a)/4)−0)^2 )) =(√((a^2 −4ab+4b^2 +3a^2 )/(16)))=(1/2)(√(a^2 −ab+b^2 )) ∵ FG=FD=GD=(1/2)(√(a^2 −ab+b^2 )) ∴ △GFD is an EQUILATERAL Triangle
$$\:^{\bullet} {Let}\:{common}\:{vertex}\:{of}\:{triangles}\:{D}=\left(\mathrm{0},\mathrm{0}\right) \\ $$$${and}\:{AD}\:{and}\:{DB}\:{are}\:{along}\:{x}-{axis}. \\ $$$$\left({AD}\:{and}\:{DB}\:{are}\:{collinear}\right) \\ $$$$\:^{\bullet} {Let}\:{each}\:{side}\:{of}\:\bigtriangleup{ADC}={a}\:{units} \\ $$$${and}\:{each}\:{side}\:{of}\:\bigtriangleup{BDE}={b}\:{units} \\ $$$$\:^{\bullet} {Let}\:{A}\:{is}\:{on}\:{left}\:{side}\:{of}\:{D}\:{and}\:{B} \\ $$$${is}\:{on}\:{right}\:{side}\:{of}\:{D} \\ $$$$\:{So}\:{A}=\left(−{a},\mathrm{0}\right)\:{and}\:{B}=\left({b},\mathrm{0}\right) \\ $$$${It}\:{can}\:{be}\:{shown}\:{easily} \\ $$$${that}\:{C}=\left(−\frac{{a}}{\mathrm{2}},\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}{a}\right)\:{and}\:{E}=\left(\frac{{b}}{\mathrm{2}},\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}{b}\right) \\ $$$${G}\:{is}\:{midpoint}\:{of}\:{BC} \\ $$$${So}\:\:{G}=\left(\:\frac{\mathrm{1}}{\mathrm{2}}\left(−\frac{{a}}{\mathrm{2}}+{b}\right),\frac{\mathrm{1}}{\mathrm{2}}\left(\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}{a}+\mathrm{0}\right)\:\right)=\left(\frac{\mathrm{2}{b}−{a}}{\mathrm{4}},\frac{\sqrt{\mathrm{3}}{a}}{\mathrm{4}}\right) \\ $$$${F}\:{is}\:{midpoint}\:{of}\:{AE} \\ $$$${So}\:{F}=\left(\frac{\mathrm{1}}{\mathrm{2}}\left(−{a}+\frac{{b}}{\mathrm{2}}\right),\frac{\mathrm{1}}{\mathrm{2}}\left(\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}{b}+\mathrm{0}\right)\right)=\left(\frac{{b}−\mathrm{2}{a}}{\mathrm{4}},\frac{\sqrt{\mathrm{3}}\:{b}}{\mathrm{4}}\right) \\ $$$${Now}\:{in}\:\bigtriangleup{FGD} \\ $$$${FG}=\sqrt{\left(\frac{\mathrm{2}{b}−{a}}{\mathrm{4}}−\frac{{b}−\mathrm{2}{a}}{\mathrm{4}}\right)^{\mathrm{2}} +\left(\frac{\sqrt{\mathrm{3}}{a}}{\mathrm{4}}−\frac{\sqrt{\mathrm{3}}\:{b}}{\mathrm{4}}\right)^{\mathrm{2}} } \\ $$$$\:\:\:\:\:\:\:\:=\sqrt{\frac{\left({b}+{a}\right)^{\mathrm{2}} }{\mathrm{16}}+\frac{\mathrm{3}\left(\:{a}−{b}\right)^{\mathrm{2}} }{\mathrm{16}}}= \\ $$$$\:\:\:\:\:\:\:\:=\frac{\sqrt{{a}^{\mathrm{2}} +\mathrm{2}{ab}+{b}^{\mathrm{2}} +\mathrm{3}{a}^{\mathrm{2}} −\mathrm{6}{ab}+\mathrm{3}{b}^{\mathrm{2}} }}{\mathrm{4}} \\ $$$$\:\:\:\:\:\:\:\:=\frac{\sqrt{\mathrm{4}{a}^{\mathrm{2}} −\mathrm{4}{ab}+\mathrm{4}{b}^{\mathrm{2}} }}{\mathrm{4}}=\frac{\mathrm{1}}{\mathrm{2}}\sqrt{{a}^{\mathrm{2}} −{ab}+{b}^{\mathrm{2}} } \\ $$$${FD}=\sqrt{\left(\frac{{b}−\mathrm{2}{a}}{\mathrm{4}}−\mathrm{0}\right)^{\mathrm{2}} +\left(\frac{\sqrt{\mathrm{3}}\:{b}}{\mathrm{4}}−\mathrm{0}\right)^{\mathrm{2}} } \\ $$$$\:\:\:\:\:\:\:\:=\sqrt{\frac{{b}^{\mathrm{2}} −\mathrm{4}{ab}+\mathrm{4}{a}^{\mathrm{2}} +\mathrm{3}{b}^{\mathrm{2}} }{\mathrm{16}}}=\frac{\mathrm{1}}{\mathrm{2}}\sqrt{{a}^{\mathrm{2}} −{ab}+{b}^{\mathrm{2}} } \\ $$$${GD}=\sqrt{\left(\frac{\mathrm{2}{b}−{a}}{\mathrm{4}}−\mathrm{0}\right)^{\mathrm{2}} +\left(\frac{\sqrt{\mathrm{3}}{a}}{\mathrm{4}}−\mathrm{0}\right)^{\mathrm{2}} } \\ $$$$\:\:\:\:\:\:\:\:=\sqrt{\frac{{a}^{\mathrm{2}} −\mathrm{4}{ab}+\mathrm{4}{b}^{\mathrm{2}} +\mathrm{3}{a}^{\mathrm{2}} }{\mathrm{16}}}=\frac{\mathrm{1}}{\mathrm{2}}\sqrt{{a}^{\mathrm{2}} −{ab}+{b}^{\mathrm{2}} } \\ $$$$\because\:\:\:{FG}={FD}={GD}=\frac{\mathrm{1}}{\mathrm{2}}\sqrt{{a}^{\mathrm{2}} −{ab}+{b}^{\mathrm{2}} } \\ $$$$\therefore\:\bigtriangleup{GFD}\:\:{is}\:{an}\:\mathcal{EQUILATERAL}\:\mathcal{T}{riangle} \\ $$
Commented by Yozzii last updated on 04/Feb/16
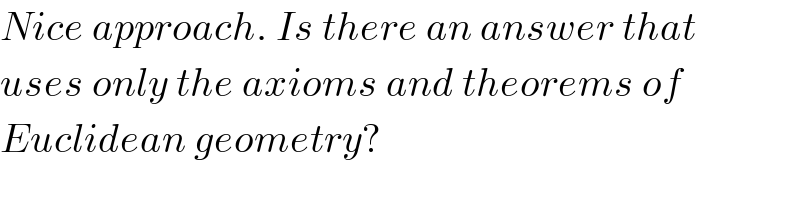
Nice approach. Is there an answer that uses only the axioms and theorems of Euclidean geometry?
$${Nice}\:{approach}.\:{Is}\:{there}\:{an}\:{answer}\:{that} \\ $$$${uses}\:{only}\:{the}\:{axioms}\:{and}\:{theorems}\:{of} \\ $$$${Euclidean}\:{geometry}? \\ $$
Commented by Rasheed Soomro last updated on 05/Feb/16
There must be axiomatic proof,but I am not successful to prove yet.
$${There}\:{must}\:{be}\:{axiomatic}\:{proof},{but}\:{I}\: \\ $$$${am}\:{not}\:{successful}\:{to}\:{prove}\:{yet}. \\ $$
Commented by Yozzii last updated on 06/Feb/16
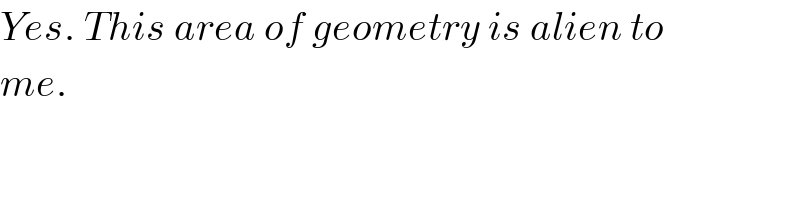
Yes. This area of geometry is alien to me.
$${Yes}.\:{This}\:{area}\:{of}\:{geometry}\:{is}\:{alien}\:{to} \\ $$$${me}. \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *