Question Number 4548 by Yozzii last updated on 07/Feb/16
Commented by Yozzii last updated on 07/Feb/16

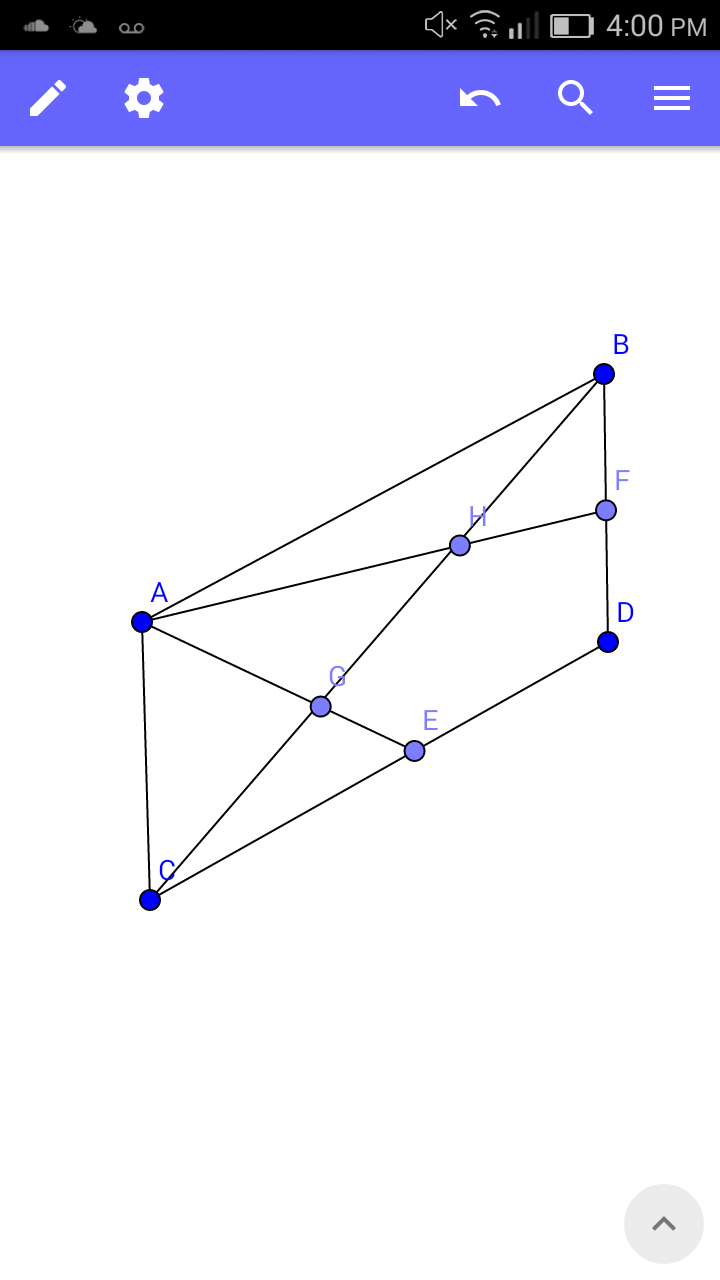
$${In}\:{the}\:{diagram}\:{is}\:{a}\:{parallelogram}\:{ABCD} \\ $$$${with}\:{diagonal}\:{CB}. \\ $$$${E}\:{and}\:{F}\:{are}\:{the}\:{midpoints}\:{of}\:{CD}\:{and} \\ $$$${BD}\:{respectively}.\:{Using}\:{vectors},\:{prove} \\ $$$${that}\:{AE}\:{and}\:{AF}\:{trisect}\:{CB}. \\ $$
Commented by Rasheed Soomro last updated on 11/Feb/16

$${I}\:{have}\:{an}\:{idea}\:{of}\:{axiomatic}\:{proof}. \\ $$$${But}\:{question}\:{requirs}\:{only}\:{proof}\:{by} \\ $$$${vectors}. \\ $$$${If}\:{an}\:{axiomatic}\:{approach}\:{may}\:{also} \\ $$$${be}\:{welcomed},\:{I}\:{can}\:{share}. \\ $$
