Question Number 4812 by sanusihammed last updated on 15/Mar/16

Commented by prakash jain last updated on 16/Mar/16
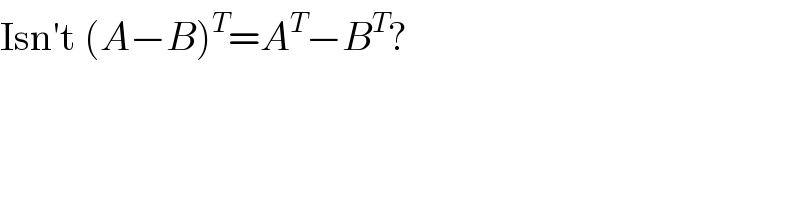
$$\mathrm{Isn}'\mathrm{t}\:\left({A}−{B}\right)^{{T}} ={A}^{{T}} −{B}^{{T}} ? \\ $$
Commented by prakash jain last updated on 15/Mar/16
![(A+3 [(1,(−1),0),(1,2,4) ])^T = [(2,1),(0,5),(3,8) ] (A+3 [(1,(−1),0),(1,2,4) ])^T = [(2,1),(0,5),(3,8) ] (A+3 [(1,(−1),0),(1,2,4) ])= [(2,1),(0,5),(3,8) ]^T = [(2,0,3),(1,5,8) ] A= [(2,0,3),(1,5,8) ]−3 [(1,(−1),0),(1,2,4) ]= [((−1),3,3),((−2),(−1),(−4)) ]](https://www.tinkutara.com/question/Q4814.png)
$$\left({A}+\mathrm{3}\begin{bmatrix}{\mathrm{1}}&{−\mathrm{1}}&{\mathrm{0}}\\{\mathrm{1}}&{\mathrm{2}}&{\mathrm{4}}\end{bmatrix}\right)^{{T}} =\begin{bmatrix}{\mathrm{2}}&{\mathrm{1}}\\{\mathrm{0}}&{\mathrm{5}}\\{\mathrm{3}}&{\mathrm{8}}\end{bmatrix} \\ $$$$\left({A}+\mathrm{3}\begin{bmatrix}{\mathrm{1}}&{−\mathrm{1}}&{\mathrm{0}}\\{\mathrm{1}}&{\mathrm{2}}&{\mathrm{4}}\end{bmatrix}\right)^{{T}} =\begin{bmatrix}{\mathrm{2}}&{\mathrm{1}}\\{\mathrm{0}}&{\mathrm{5}}\\{\mathrm{3}}&{\mathrm{8}}\end{bmatrix} \\ $$$$\left({A}+\mathrm{3}\begin{bmatrix}{\mathrm{1}}&{−\mathrm{1}}&{\mathrm{0}}\\{\mathrm{1}}&{\mathrm{2}}&{\mathrm{4}}\end{bmatrix}\right)=\begin{bmatrix}{\mathrm{2}}&{\mathrm{1}}\\{\mathrm{0}}&{\mathrm{5}}\\{\mathrm{3}}&{\mathrm{8}}\end{bmatrix}^{{T}} =\begin{bmatrix}{\mathrm{2}}&{\mathrm{0}}&{\mathrm{3}}\\{\mathrm{1}}&{\mathrm{5}}&{\mathrm{8}}\end{bmatrix} \\ $$$$ \\ $$$${A}=\begin{bmatrix}{\mathrm{2}}&{\mathrm{0}}&{\mathrm{3}}\\{\mathrm{1}}&{\mathrm{5}}&{\mathrm{8}}\end{bmatrix}−\mathrm{3}\begin{bmatrix}{\mathrm{1}}&{−\mathrm{1}}&{\mathrm{0}}\\{\mathrm{1}}&{\mathrm{2}}&{\mathrm{4}}\end{bmatrix}=\begin{bmatrix}{−\mathrm{1}}&{\mathrm{3}}&{\mathrm{3}}\\{−\mathrm{2}}&{−\mathrm{1}}&{−\mathrm{4}}\end{bmatrix} \\ $$
Commented by Yozzii last updated on 16/Mar/16

$$\left(\mathrm{3}{A}^{{T}} +\mathrm{2}\begin{pmatrix}{\mathrm{1}}&{\mathrm{0}}\\{\mathrm{0}}&{\mathrm{2}}\end{pmatrix}\right)^{{T}} =\begin{pmatrix}{\mathrm{8}}&{\mathrm{0}}\\{\mathrm{3}}&{\mathrm{1}}\end{pmatrix} \\ $$$${Matrix}\:{addition}\:{is}\:{only}\:{possible}\:{between} \\ $$$${matrices}\:{of}\:{equal}\:{dimensions}\:{so}\:{that} \\ $$$${addition}\:{of}\:{corresponding}\:{elements} \\ $$$${occurs}.\:{So}\:{in}\:\left({ii}\right)\:{we}\:{could}\:{let}\:{A}\:{be}\:{a}\:\mathrm{2}×\mathrm{2}\: \\ $$$${matrix}\:{of}\:{the}\:{form}\: \\ $$$${A}=\begin{pmatrix}{{a}}&{{b}}\\{{c}}&{{d}}\end{pmatrix}\:\Rightarrow{A}^{{T}} =\begin{pmatrix}{{a}}&{{c}}\\{{b}}&{{d}}\end{pmatrix}\Rightarrow\mathrm{3}{A}^{{T}} =\begin{pmatrix}{\mathrm{3}{a}}&{\mathrm{3}{c}}\\{\mathrm{3}{b}}&{\mathrm{3}{d}}\end{pmatrix} \\ $$$$\Rightarrow\mathrm{3}{A}^{{T}} +\begin{pmatrix}{\mathrm{2}}&{\mathrm{0}}\\{\mathrm{0}}&{\mathrm{4}}\end{pmatrix}=\begin{pmatrix}{\mathrm{3}{a}+\mathrm{2}}&{\mathrm{3}{c}}\\{\mathrm{3}{b}}&{\mathrm{3}{d}+\mathrm{4}}\end{pmatrix} \\ $$$$\therefore\left(\mathrm{3}{A}^{{T}} +\mathrm{2}\begin{pmatrix}{\mathrm{1}}&{\mathrm{0}}\\{\mathrm{0}}&{\mathrm{2}}\end{pmatrix}\right)^{{T}} =\begin{pmatrix}{\mathrm{3}{a}+\mathrm{2}}&{\mathrm{3}{b}}\\{\mathrm{3}{c}}&{\mathrm{3}{d}+\mathrm{4}}\end{pmatrix}=\begin{pmatrix}{\mathrm{8}}&{\mathrm{0}}\\{\mathrm{3}}&{\mathrm{1}}\end{pmatrix} \\ $$$${Equating}\:{elements}\:{we}\:{get} \\ $$$${a}=\mathrm{2},{b}=\mathrm{0},{c}=\mathrm{1}\:{and}\:{d}=−\mathrm{1}.\:{Hence}\:{A}\:{is}\:{given}\:{by} \\ $$$${A}=\begin{pmatrix}{\mathrm{2}}&{\mathrm{0}}\\{\mathrm{1}}&{−\mathrm{1}}\end{pmatrix}. \\ $$$${Checking}:\:\mathrm{3}{A}^{{T}} =\begin{pmatrix}{\mathrm{6}}&{\mathrm{3}}\\{\mathrm{0}}&{−\mathrm{3}}\end{pmatrix} \\ $$$$\mathrm{3}{A}^{{T}} +\begin{pmatrix}{\mathrm{2}}&{\mathrm{0}}\\{\mathrm{0}}&{\mathrm{4}}\end{pmatrix}=\begin{pmatrix}{\mathrm{8}}&{\mathrm{3}}\\{\mathrm{0}}&{\mathrm{1}}\end{pmatrix}\Rightarrow\left(\mathrm{3}{A}^{{T}} +\mathrm{2}\begin{pmatrix}{\mathrm{1}}&{\mathrm{0}}\\{\mathrm{0}}&{\mathrm{2}}\end{pmatrix}\right)^{{T}} =\begin{pmatrix}{\mathrm{8}}&{\mathrm{0}}\\{\mathrm{3}}&{\mathrm{1}}\end{pmatrix}. \\ $$$${Alternatively}\:{you}\:{could}\:{utilise}\:{the} \\ $$$${idea}\:{of}\:{the}\:{trasposition}\:\:{of}\:{matrices} \\ $$$${to}\:{find}\:{A}\:{by}\:{a}\:{series}\:{of}\:{operations}\: \\ $$$${on}\:{the}\:{original}\:{equation}.\:{Mr}.\:{Jain} \\ $$$${has}\:{done}\:{this}\:{in}\:{his}\:{answer}\:{for}\:\left({i}\right). \\ $$$$\left({iii}\right)\:\:{can}\:{be}\:{done}\:{simply}\:{by}\:{such}\: \\ $$$${a}\:{manipulation}. \\ $$
Commented by prakash jain last updated on 16/Mar/16
![(2A^T −5 [(1,0),((−1),2) ])^T =4A−9 [(1,1),((−2),0) ] 2A−5 [(1,(−1)),(0,2) ]=4A−9 [(1,1),((−2),0) ] 2A=9 [(1,1),((−2),0) ]−5 [(1,(−1)),(0,2) ] 2A= [(4,(14)),((−18),(−10)) ] A= [(2,7),((−9),(−5)) ]](https://www.tinkutara.com/question/Q4830.png)
$$\left(\mathrm{2}{A}^{{T}} −\mathrm{5}\begin{bmatrix}{\mathrm{1}}&{\mathrm{0}}\\{−\mathrm{1}}&{\mathrm{2}}\end{bmatrix}\right)^{{T}} =\mathrm{4}{A}−\mathrm{9}\begin{bmatrix}{\mathrm{1}}&{\mathrm{1}}\\{−\mathrm{2}}&{\mathrm{0}}\end{bmatrix} \\ $$$$\mathrm{2}{A}−\mathrm{5}\begin{bmatrix}{\mathrm{1}}&{−\mathrm{1}}\\{\mathrm{0}}&{\mathrm{2}}\end{bmatrix}=\mathrm{4}{A}−\mathrm{9}\begin{bmatrix}{\mathrm{1}}&{\mathrm{1}}\\{−\mathrm{2}}&{\mathrm{0}}\end{bmatrix} \\ $$$$\mathrm{2}{A}=\mathrm{9}\begin{bmatrix}{\mathrm{1}}&{\mathrm{1}}\\{−\mathrm{2}}&{\mathrm{0}}\end{bmatrix}−\mathrm{5}\begin{bmatrix}{\mathrm{1}}&{−\mathrm{1}}\\{\mathrm{0}}&{\mathrm{2}}\end{bmatrix} \\ $$$$\mathrm{2}{A}=\begin{bmatrix}{\mathrm{4}}&{\mathrm{14}}\\{−\mathrm{18}}&{−\mathrm{10}}\end{bmatrix} \\ $$$${A}=\begin{bmatrix}{\mathrm{2}}&{\mathrm{7}}\\{−\mathrm{9}}&{−\mathrm{5}}\end{bmatrix} \\ $$
Commented by Yozzii last updated on 16/Mar/16
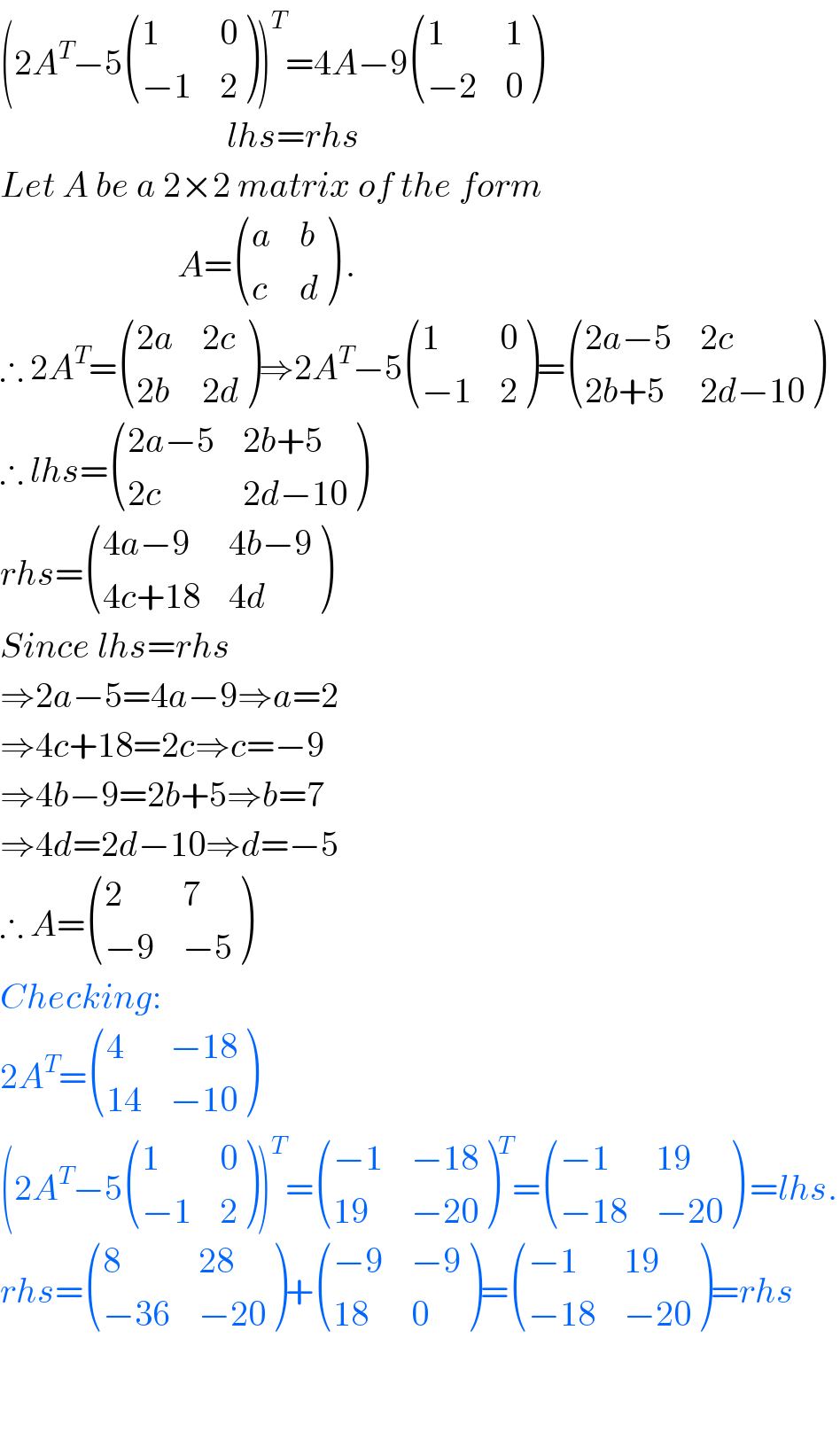
$$\left(\mathrm{2}{A}^{{T}} −\mathrm{5}\begin{pmatrix}{\mathrm{1}}&{\mathrm{0}}\\{−\mathrm{1}}&{\mathrm{2}}\end{pmatrix}\right)^{{T}} =\mathrm{4}{A}−\mathrm{9}\begin{pmatrix}{\mathrm{1}}&{\mathrm{1}}\\{−\mathrm{2}}&{\mathrm{0}}\end{pmatrix} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{lhs}={rhs} \\ $$$${Let}\:{A}\:{be}\:{a}\:\mathrm{2}×\mathrm{2}\:{matrix}\:{of}\:{the}\:{form} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{A}=\begin{pmatrix}{{a}}&{{b}}\\{{c}}&{{d}}\end{pmatrix}\:. \\ $$$$\therefore\:\mathrm{2}{A}^{{T}} =\begin{pmatrix}{\mathrm{2}{a}}&{\mathrm{2}{c}}\\{\mathrm{2}{b}}&{\mathrm{2}{d}}\end{pmatrix}\Rightarrow\mathrm{2}{A}^{{T}} −\mathrm{5}\begin{pmatrix}{\mathrm{1}}&{\mathrm{0}}\\{−\mathrm{1}}&{\mathrm{2}}\end{pmatrix}=\begin{pmatrix}{\mathrm{2}{a}−\mathrm{5}}&{\mathrm{2}{c}}\\{\mathrm{2}{b}+\mathrm{5}}&{\mathrm{2}{d}−\mathrm{10}}\end{pmatrix} \\ $$$$\therefore\:{lhs}=\begin{pmatrix}{\mathrm{2}{a}−\mathrm{5}}&{\mathrm{2}{b}+\mathrm{5}}\\{\mathrm{2}{c}}&{\mathrm{2}{d}−\mathrm{10}}\end{pmatrix} \\ $$$${rhs}=\begin{pmatrix}{\mathrm{4}{a}−\mathrm{9}}&{\mathrm{4}{b}−\mathrm{9}}\\{\mathrm{4}{c}+\mathrm{18}}&{\mathrm{4}{d}}\end{pmatrix} \\ $$$${Since}\:{lhs}={rhs} \\ $$$$\Rightarrow\mathrm{2}{a}−\mathrm{5}=\mathrm{4}{a}−\mathrm{9}\Rightarrow{a}=\mathrm{2} \\ $$$$\Rightarrow\mathrm{4}{c}+\mathrm{18}=\mathrm{2}{c}\Rightarrow{c}=−\mathrm{9} \\ $$$$\Rightarrow\mathrm{4}{b}−\mathrm{9}=\mathrm{2}{b}+\mathrm{5}\Rightarrow{b}=\mathrm{7} \\ $$$$\Rightarrow\mathrm{4}{d}=\mathrm{2}{d}−\mathrm{10}\Rightarrow{d}=−\mathrm{5} \\ $$$$\therefore\:{A}=\begin{pmatrix}{\mathrm{2}}&{\mathrm{7}}\\{−\mathrm{9}}&{−\mathrm{5}}\end{pmatrix} \\ $$$${Checking}: \\ $$$$\mathrm{2}{A}^{{T}} =\begin{pmatrix}{\mathrm{4}}&{−\mathrm{18}}\\{\mathrm{14}}&{−\mathrm{10}}\end{pmatrix} \\ $$$$\left(\mathrm{2}{A}^{{T}} −\mathrm{5}\begin{pmatrix}{\mathrm{1}}&{\mathrm{0}}\\{−\mathrm{1}}&{\mathrm{2}}\end{pmatrix}\right)^{{T}} =\begin{pmatrix}{−\mathrm{1}}&{−\mathrm{18}}\\{\mathrm{19}}&{−\mathrm{20}}\end{pmatrix}^{{T}} =\begin{pmatrix}{−\mathrm{1}}&{\mathrm{19}}\\{−\mathrm{18}}&{−\mathrm{20}}\end{pmatrix}\:={lhs}. \\ $$$${rhs}=\begin{pmatrix}{\mathrm{8}}&{\mathrm{28}}\\{−\mathrm{36}}&{−\mathrm{20}}\end{pmatrix}+\begin{pmatrix}{−\mathrm{9}}&{−\mathrm{9}}\\{\mathrm{18}}&{\mathrm{0}}\end{pmatrix}=\begin{pmatrix}{−\mathrm{1}}&{\mathrm{19}}\\{−\mathrm{18}}&{−\mathrm{20}}\end{pmatrix}={rhs} \\ $$$$ \\ $$$$ \\ $$
Commented by Yozzii last updated on 16/Mar/16
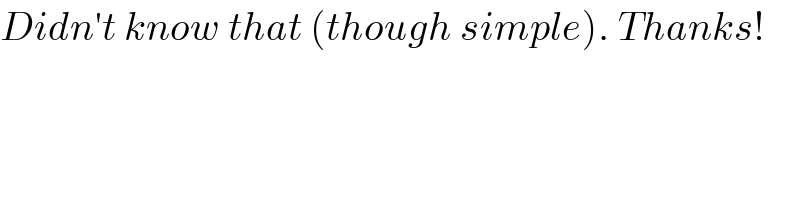
$${Didn}'{t}\:{know}\:{that}\:\left({though}\:{simple}\right).\:{Thanks}! \\ $$
