Question Number 4954 by Dnilka228 last updated on 26/Mar/16

$$ \\ $$$$ \\ $$
Commented by Dnilka228 last updated on 26/Mar/16
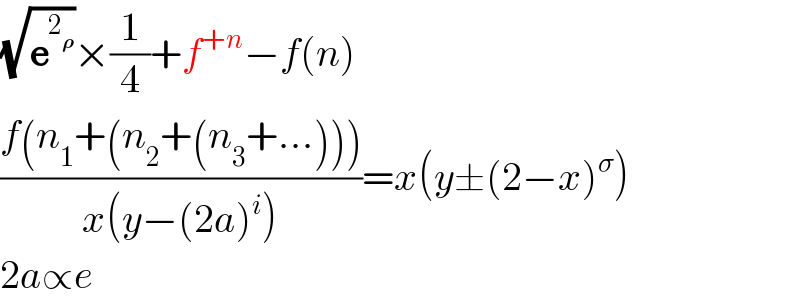
$$\sqrt{\boldsymbol{\mathrm{e}}^{\mathrm{2}_{\boldsymbol{\rho}} } }×\frac{\mathrm{1}}{\mathrm{4}}+{f}^{+{n}} −{f}\left({n}\right) \\ $$$$\frac{{f}\left({n}_{\mathrm{1}} +\left({n}_{\mathrm{2}} +\left({n}_{\mathrm{3}} +…\right)\right)\right)}{{x}\left({y}−\left(\mathrm{2}{a}\right)^{{i}} \right)}={x}\left({y}\pm\left(\mathrm{2}−{x}\right)^{\sigma} \right) \\ $$$$\mathrm{2}{a}\propto{e} \\ $$
Answered by 123456 last updated on 26/Mar/16

$${x}_{{n}+\mathrm{1}} ={xx}_{{n}} +\alpha{yy}_{{n}} \\ $$$${y}_{{n}+\mathrm{1}} ={x}_{{n}} {y}+{xy}_{{n}} +\beta{yy}_{{n}} \\ $$$${x}_{\mathrm{0}} =\mathrm{1} \\ $$$${y}_{\mathrm{0}} =\mathrm{0} \\ $$
Answered by FilupSmith last updated on 27/Mar/16
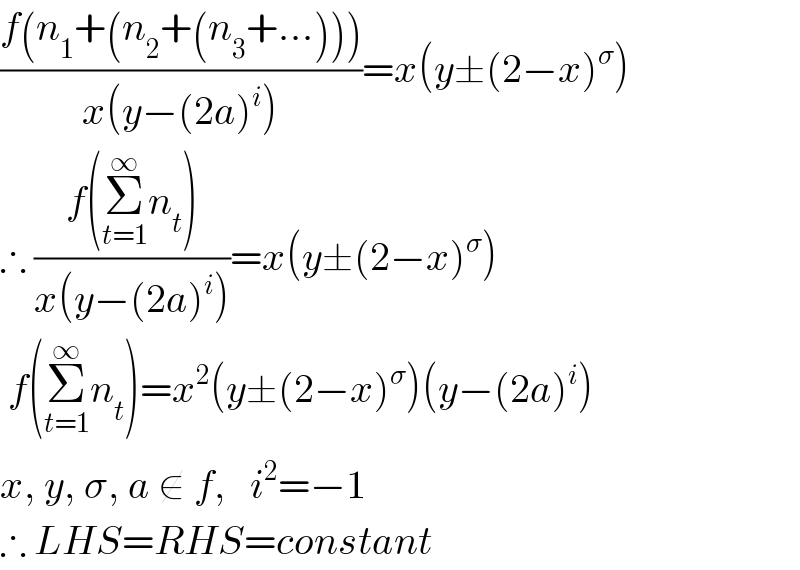
$$\frac{{f}\left({n}_{\mathrm{1}} +\left({n}_{\mathrm{2}} +\left({n}_{\mathrm{3}} +…\right)\right)\right)}{{x}\left({y}−\left(\mathrm{2}{a}\right)^{{i}} \right)}={x}\left({y}\pm\left(\mathrm{2}−{x}\right)^{\sigma} \right) \\ $$$$\therefore\:\frac{{f}\left(\underset{{t}=\mathrm{1}} {\overset{\infty} {\sum}}{n}_{{t}} \right)}{{x}\left({y}−\left(\mathrm{2}{a}\right)^{{i}} \right)}={x}\left({y}\pm\left(\mathrm{2}−{x}\right)^{\sigma} \right) \\ $$$$\:{f}\left(\underset{{t}=\mathrm{1}} {\overset{\infty} {\sum}}{n}_{{t}} \right)={x}^{\mathrm{2}} \left({y}\pm\left(\mathrm{2}−{x}\right)^{\sigma} \right)\left({y}−\left(\mathrm{2}{a}\right)^{{i}} \right) \\ $$$${x},\:{y},\:\sigma,\:{a}\:\notin\:{f},\:\:\:{i}^{\mathrm{2}} =−\mathrm{1} \\ $$$$\therefore\:{LHS}={RHS}={constant} \\ $$
