Question Number 4971 by Rasheed Soomro last updated on 28/Mar/16

Commented by Rasheed Soomro last updated on 28/Mar/16

$${Write}\:{process}\:{also}. \\ $$
Commented by Rasheed Soomro last updated on 29/Mar/16

$${How}? \\ $$
Commented by Yozzii last updated on 29/Mar/16

$${one}−{quarter}\:{the}\:{area}\:{of}\:{the}\:{square} \\ $$
Commented by Yozzii last updated on 29/Mar/16

$${The}\:{lines}\:{from}\:{the}\:{midpoints}\:{on}\:{the}\:{sides}\:{of}\:{the}\:{square} \\ $$$${trissect}\:{the}\:{hypotenuse}\:{of}\:{the}\:{smaller}\:{triangle}.\:{I}\:{was} \\ $$$${trying}\:{to}\:{upload}\:{my}\:{answer}\:{as}\:{pics} \\ $$$${but}\:{it}\:{failed}\:{to}\:{upload}. \\ $$
Commented by Yozzii last updated on 29/Mar/16

Commented by Yozzii last updated on 30/Mar/16

$${The}\:{inner}\:{triangles}\:{are}\:{reflections}\:{of} \\ $$$${each}\:{other}\:{in}\:{the}\:{diagonal}.\:{The}\:{diagonal} \\ $$$${of}\:{the}\:{square}\:{is}\:{also}\:{trissected}.\:{So} \\ $$$${ST}\:\:{one}\:{third}\:{AC}.\:{ST},{AC},{RQ}\:{and}\:{NJ} \\ $$$${are}\:{parallel}.\:{So},\:{the}\:{area}\:{you}\:{want} \\ $$$${is}\:{made}\:{up}\:{of}\:{areas}\:{of}\:{two}\:{congruent} \\ $$$${trapezia}.\:\bigtriangleup{ROQ}\:{is}\:{isosceles}\:{so}\: \\ $$$${the}\:{line}\:{from}\:{O}\:{that}\:{falls}\:{on}\:{RQ}\: \\ $$$${normally}\:{bissects}\:{the}\:{line}\:{RQ}. \\ $$$${Using}\:{this},\:{the}\:{length}\:{OM}\:{is}\:{found} \\ $$$${to}\:{be}\:\frac{{a}\sqrt{\mathrm{2}}}{\mathrm{4}}.\:{Likewise},\:{BF}=\frac{{a}\sqrt{\mathrm{2}}}{\mathrm{4}}\:{since} \\ $$$$\bigtriangleup{ROQ}\approxeq\bigtriangleup{BNJ}.\:{So},\:{MF}={OB}−\left({BF}+{OM}\right) \\ $$$${MF}={a}\sqrt{\mathrm{2}}−\frac{\mathrm{2}{a}\sqrt{\mathrm{2}}}{\mathrm{4}}=\frac{{a}\sqrt{\mathrm{2}}}{\mathrm{2}}. \\ $$$$\frac{{MF}}{\mathrm{2}}\:{is}\:{the}\:'{height}'\:{of}\:{each}\:{trapezium}. \\ $$$${You}\:{see}\:{in}\:{my}\:{diagram}\:{that}\:{LK}=\frac{\mathrm{1}}{\mathrm{3}}{RQ}=\frac{{a}\sqrt{\mathrm{2}}}{\mathrm{6}} \\ $$$${and}\:{ST}=\frac{{a}\sqrt{\mathrm{2}}}{\mathrm{3}}.\: \\ $$$$\therefore\:{A}_{{t}} =\frac{\mathrm{1}}{\mathrm{2}}\left({LK}+{ST}\right)\frac{{MF}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{2}}\left({UV}+{ST}\right)\frac{{MF}}{\mathrm{2}} \\ $$$${A}_{{t}} =\frac{{MF}}{\mathrm{4}}\left({LK}+{UV}+\mathrm{2}{ST}\right) \\ $$$${A}_{{t}} =\frac{{a}\sqrt{\mathrm{2}}/\mathrm{2}}{\mathrm{4}}\left(\mathrm{2}{LK}+\mathrm{2}{ST}\right) \\ $$$${A}_{{t}} =\frac{{a}\sqrt{\mathrm{2}}}{\mathrm{4}}\left(\frac{{a}\sqrt{\mathrm{2}}}{\mathrm{6}}+\frac{{a}\sqrt{\mathrm{2}}}{\mathrm{3}}\right) \\ $$$${A}_{{t}} =\frac{\mathrm{2}{a}^{\mathrm{2}} }{\mathrm{4}}\left(\frac{\mathrm{9}}{\mathrm{18}}\right)=\frac{{a}^{\mathrm{2}} }{\mathrm{4}}. \\ $$
Commented by Yozzii last updated on 30/Mar/16

$${The}\:{original}\:{solution}\:{I}\:{wanted}\:{to}\:{share} \\ $$$${is}\:{a}\:{bit}\:{lengthy}\:{because}\:{with}\:{only}\:{assuming} \\ $$$${that}\:{the}\:{figure}\:{is}\:{a}\:{square}\:{and}\:{that} \\ $$$${the}\:{large}\:{inner}\:{triangles}\:{have}\:{vertices} \\ $$$${as}\:\mathrm{2}\:{side}\:{mid}−{points}\:{and}\:\mathrm{1}\:{vertex}\:{of}\:{the} \\ $$$${square},\:{I}\:{had}\:{to}\:{prove}\:{everything} \\ $$$${else},\:{such}\:{as}\:{parallelism}\:{and}\:{trissection}. \\ $$$${It}\:{wasn}'{t}\:{specified}\:{if}\:{the}\:{figure}\:{was}\:{a}\:{rectangle} \\ $$$${or}\:{square}\:{or}\:{if}\:{those}\:{vertices}\:{are}\: \\ $$$${really}\:{midpoints}\:{of}\:{the}\:{sides}\:{of}\:{the}\: \\ $$$${figure}.\:{One}\:{could}\:{attempt}\:{the}\: \\ $$$${general}\:{case}\:{where}\:{the}\:{vertices}\:{of}\: \\ $$$${the}\:{triangle}\:{come}\:{from}\:{one}\:{rectangle} \\ $$$${vertex}\:{and}\:{two}\:{points}\:{that}\:{lie}\:{anywhere} \\ $$$${on}\:{two}\:{sides}\:{of}\:{the}\:{rectangle}\:{that}\:{do}\:{not}\:{contain}\:{the} \\ $$$${rectangle}\:{vertex}. \\ $$$$ \\ $$
Answered by Rasheed Soomro last updated on 30/Mar/16
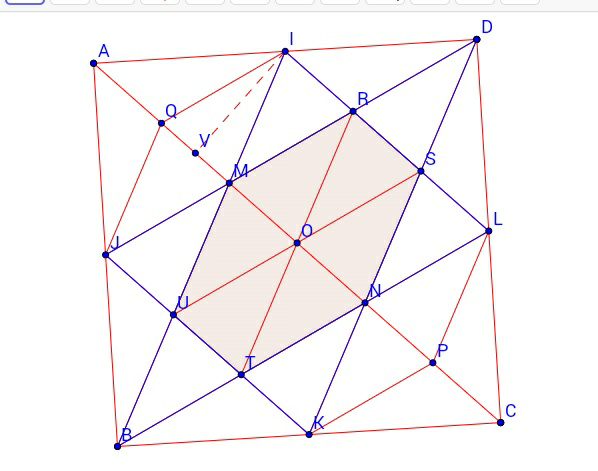
Commented by Rasheed Soomro last updated on 30/Mar/16

$${All}\:{small}\:{triangles}\:{have}\:{equal} \\ $$$${area}.\:{Some}\:{triangles}\:{are}\:{congruent} \\ $$$${also}.\:{There}\:{are}\:{some}\:\:{triangles},{which}\:{are} \\ $$$${not}\:{congruent}\:{but}\:{despite}\:{this}\:\:{they}\:{have}\:{equal} \\ $$$${area},\:{because}\:{they}\:{have}\:{equal}\:{bases} \\ $$$${and}\:{altitudes}.{For}\:{example}: \\ $$$$\bigtriangleup{AIQ}\ncong\bigtriangleup{IQM} \\ $$$${But}\:{these}\:{triangles}\:{have}\:{equal}\:{bases} \\ $$$${AQ}={QM}\:{and}\:{common}\:{altitude}\:{IV} \\ $$$${and}\:{hence}\:{equal}\:{area}. \\ $$$${Now}\:{number}\:{of}\:{triangles}\:{in}\:{whole} \\ $$$${is}\:\mathrm{24}, \\ $$$${Number}\:{of}\:{triangles}\:{in}\:{shaded}\:{area} \\ $$$${is}\:\mathrm{6}. \\ $$$$\therefore\:{The}\:{shaded}\:{area}\:{is}\:\frac{\mathrm{6}}{\mathrm{24}}=\frac{\mathrm{1}}{\mathrm{4}}\:{part}\:{of}\:{the} \\ $$$${whole}. \\ $$$$ \\ $$
Commented by Yozzii last updated on 30/Mar/16

$${Nice}. \\ $$
Commented by FilupSmith last updated on 31/Mar/16

$${A}\mathrm{mazing}\:\mathrm{and}\:\mathrm{simple}\:\mathrm{to}\:\mathrm{understand}! \\ $$
Answered by Rasheed Soomro last updated on 31/Mar/16

Commented by Rasheed Soomro last updated on 31/Mar/16

$${An}\:{other}\:{answer}: \\ $$$$\mathrm{H},\mathrm{I},\mathrm{J}\:\&\:\mathrm{K}\:{are}\:{midpoints}\:{of}\:{the} \\ $$$${sides}\:{of}\:{the}\:\Box\mathrm{ABCD}\:{and}\:{it}\:{can} \\ $$$${be}\:{shown}\:{that}: \\ $$$$\blacksquare\mathrm{HIJK}=\frac{\mathrm{1}}{\mathrm{2}}\:{of}\:\blacksquare\mathrm{ABCD}\:\left(\blacksquare\:{for}\:{area}\:\:\:\:\:\:\:\:\left(\mathrm{I}\right)\right. \\ $$$$\left.{of}\:{square}\right) \\ $$$${Now}, \\ $$$$\Box\mathrm{HIJK}\:{contains}\:\:\mathrm{24}\:{small}\:{triangles} \\ $$$${and} \\ $$$${polygon}\:\mathrm{PQRSTU}\:{contains}\:\mathrm{12}\:{small} \\ $$$${triangles}. \\ $$$${So}, \\ $$$${Area}\:\mathrm{PQRSTU}=\frac{\mathrm{12}}{\mathrm{24}}=\frac{\mathrm{1}}{\mathrm{2}}\:{of}\:\blacksquare\mathrm{HIJK}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\left(\mathrm{II}\right) \\ $$$${From}\:\left(\mathrm{I}\right)\:\&\:\left(\mathrm{II}\right) \\ $$$${Area}\:\mathrm{PQRSTU}=\frac{\mathrm{1}}{\mathrm{2}}×\frac{\mathrm{1}}{\mathrm{2}}=\frac{\mathrm{1}}{\mathrm{4}}\:{of}\:\blacksquare\mathrm{ABCD} \\ $$
