Menu Close

Question-5119

Tinku Tara 0 Comments
Pin




Question Number 5119 by sanusihammed last updated on 14/Apr/16
Commented by 123456 last updated on 15/Apr/16
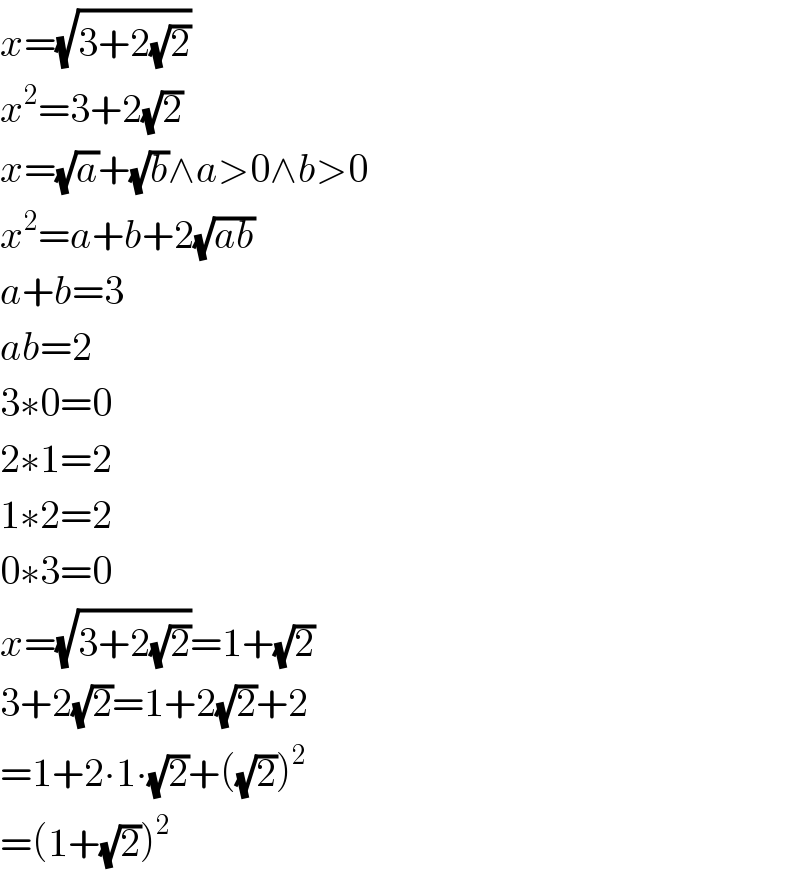
x=(√(3+2(√2))) x^2 =3+2(√2) x=(√a)+(√b)∧a>0∧b>0 x^2 =a+b+2(√(ab)) a+b=3 ab=2 3∗0=0 2∗1=2 1∗2=2 0∗3=0 x=(√(3+2(√2)))=1+(√2) 3+2(√2)=1+2(√2)+2 =1+2∙1∙(√2)+((√2))^2 =(1+(√2))^2
$${x}=\sqrt{\mathrm{3}+\mathrm{2}\sqrt{\mathrm{2}}} \\ $$$${x}^{\mathrm{2}} =\mathrm{3}+\mathrm{2}\sqrt{\mathrm{2}} \\ $$$${x}=\sqrt{{a}}+\sqrt{{b}}\wedge{a}>\mathrm{0}\wedge{b}>\mathrm{0} \\ $$$${x}^{\mathrm{2}} ={a}+{b}+\mathrm{2}\sqrt{{ab}} \\ $$$${a}+{b}=\mathrm{3} \\ $$$${ab}=\mathrm{2} \\ $$$$\mathrm{3}\ast\mathrm{0}=\mathrm{0} \\ $$$$\mathrm{2}\ast\mathrm{1}=\mathrm{2} \\ $$$$\mathrm{1}\ast\mathrm{2}=\mathrm{2} \\ $$$$\mathrm{0}\ast\mathrm{3}=\mathrm{0} \\ $$$${x}=\sqrt{\mathrm{3}+\mathrm{2}\sqrt{\mathrm{2}}}=\mathrm{1}+\sqrt{\mathrm{2}} \\ $$$$\mathrm{3}+\mathrm{2}\sqrt{\mathrm{2}}=\mathrm{1}+\mathrm{2}\sqrt{\mathrm{2}}+\mathrm{2} \\ $$$$=\mathrm{1}+\mathrm{2}\centerdot\mathrm{1}\centerdot\sqrt{\mathrm{2}}+\left(\sqrt{\mathrm{2}}\right)^{\mathrm{2}} \\ $$$$=\left(\mathrm{1}+\sqrt{\mathrm{2}}\right)^{\mathrm{2}} \\ $$
Commented by Yozzii last updated on 16/Apr/16
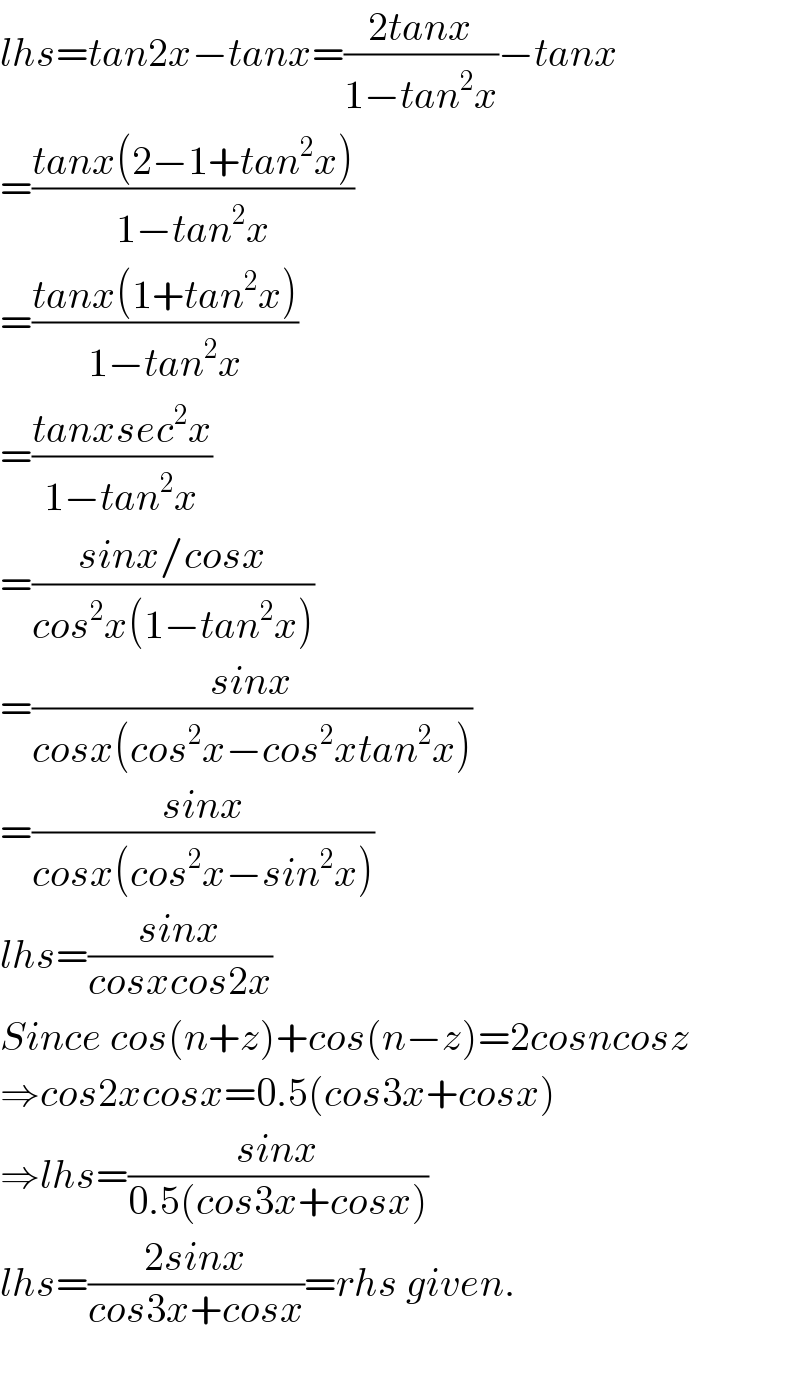
lhs=tan2x−tanx=((2tanx)/(1−tan^2 x))−tanx =((tanx(2−1+tan^2 x))/(1−tan^2 x)) =((tanx(1+tan^2 x))/(1−tan^2 x)) =((tanxsec^2 x)/(1−tan^2 x)) =((sinx/cosx)/(cos^2 x(1−tan^2 x))) =((sinx)/(cosx(cos^2 x−cos^2 xtan^2 x))) =((sinx)/(cosx(cos^2 x−sin^2 x))) lhs=((sinx)/(cosxcos2x)) Since cos(n+z)+cos(n−z)=2cosncosz ⇒cos2xcosx=0.5(cos3x+cosx) ⇒lhs=((sinx)/(0.5(cos3x+cosx))) lhs=((2sinx)/(cos3x+cosx))=rhs given.
$${lhs}={tan}\mathrm{2}{x}−{tanx}=\frac{\mathrm{2}{tanx}}{\mathrm{1}−{tan}^{\mathrm{2}} {x}}−{tanx} \\ $$$$=\frac{{tanx}\left(\mathrm{2}−\mathrm{1}+{tan}^{\mathrm{2}} {x}\right)}{\mathrm{1}−{tan}^{\mathrm{2}} {x}} \\ $$$$=\frac{{tanx}\left(\mathrm{1}+{tan}^{\mathrm{2}} {x}\right)}{\mathrm{1}−{tan}^{\mathrm{2}} {x}} \\ $$$$=\frac{{tanxsec}^{\mathrm{2}} {x}}{\mathrm{1}−{tan}^{\mathrm{2}} {x}} \\ $$$$=\frac{{sinx}/{cosx}}{{cos}^{\mathrm{2}} {x}\left(\mathrm{1}−{tan}^{\mathrm{2}} {x}\right)} \\ $$$$=\frac{{sinx}}{{cosx}\left({cos}^{\mathrm{2}} {x}−{cos}^{\mathrm{2}} {xtan}^{\mathrm{2}} {x}\right)} \\ $$$$=\frac{{sinx}}{{cosx}\left({cos}^{\mathrm{2}} {x}−{sin}^{\mathrm{2}} {x}\right)} \\ $$$${lhs}=\frac{{sinx}}{{cosxcos}\mathrm{2}{x}} \\ $$$${Since}\:{cos}\left({n}+{z}\right)+{cos}\left({n}−{z}\right)=\mathrm{2}{cosncosz} \\ $$$$\Rightarrow{cos}\mathrm{2}{xcosx}=\mathrm{0}.\mathrm{5}\left({cos}\mathrm{3}{x}+{cosx}\right) \\ $$$$\Rightarrow{lhs}=\frac{{sinx}}{\mathrm{0}.\mathrm{5}\left({cos}\mathrm{3}{x}+{cosx}\right)} \\ $$$${lhs}=\frac{\mathrm{2}{sinx}}{{cos}\mathrm{3}{x}+{cosx}}={rhs}\:{given}. \\ $$$$ \\ $$
Answered by Rasheed Soomro last updated on 08/May/16
1(a) log_x 2^x +log_2 y+5=0 ∧ xy=(1/4) log_x 2^x +log_2 y+5=0 ∧ log_2 (xy)=log_2 (2^(−2) ) xlog_x 2+log_2 y+5=0 ∧ log_2 x+log_2 y=−2log_2 2 (x/(log_2 x))+log_2 y+5=0 ∧ log_2 x+log_2 y=−2 (x/(log_2 x))+log_2 y+5=0 ∧ log_2 y=−2−log_2 x (x/(log_2 x))+(−2−log_2 x)+5=0 (x/(log_2 x))−log_2 x+3=0 ((xlog_2 2)/(log_2 x))−log_2 x+3log_2 2=0 ((log_2 2^x )/(log_2 x))−log_2 x+log_2 2^3 =0 log_2 (2^x )^(log_2 x) −log_2 x+log_2 2^3 =0 log_2 [(((2^x )^(log_2 x) )/x)×8]=log_2 1 (((2^x )^(log_2 x) )/x)×8=1 2^3 ×(2^x )^(log_2 x) =x 2^(3+xlog_2 x) =x log_2 2^(3+xlog_2 x) =log x 3+xlog_2 x=log_2 x log_2 x−xlog_2 x=3 (log_2 x)(1−x)=3 C^(ontinue)
$$\mathrm{1}\left(\mathrm{a}\right) \\ $$$$\mathrm{log}_{\mathrm{x}} \mathrm{2}^{\mathrm{x}} +\mathrm{log}_{\mathrm{2}} \mathrm{y}+\mathrm{5}=\mathrm{0}\:\wedge\:\mathrm{xy}=\frac{\mathrm{1}}{\mathrm{4}} \\ $$$$\mathrm{log}_{\mathrm{x}} \mathrm{2}^{\mathrm{x}} +\mathrm{log}_{\mathrm{2}} \mathrm{y}+\mathrm{5}=\mathrm{0}\:\wedge\:\mathrm{log}_{\mathrm{2}} \left(\mathrm{xy}\right)=\mathrm{log}_{\mathrm{2}} \left(\mathrm{2}^{−\mathrm{2}} \right) \\ $$$$\mathrm{xlog}_{\mathrm{x}} \mathrm{2}+\mathrm{log}_{\mathrm{2}} \mathrm{y}+\mathrm{5}=\mathrm{0}\:\wedge\:\mathrm{log}_{\mathrm{2}} \mathrm{x}+\mathrm{log}_{\mathrm{2}} \mathrm{y}=−\mathrm{2log}_{\mathrm{2}} \mathrm{2} \\ $$$$\frac{\mathrm{x}}{\mathrm{log}_{\mathrm{2}} \mathrm{x}}+\mathrm{log}_{\mathrm{2}} \mathrm{y}+\mathrm{5}=\mathrm{0}\:\wedge\:\mathrm{log}_{\mathrm{2}} \mathrm{x}+\mathrm{log}_{\mathrm{2}} \mathrm{y}=−\mathrm{2} \\ $$$$\frac{\mathrm{x}}{\mathrm{log}_{\mathrm{2}} \mathrm{x}}+\mathrm{log}_{\mathrm{2}} \mathrm{y}+\mathrm{5}=\mathrm{0}\:\wedge\:\mathrm{log}_{\mathrm{2}} \mathrm{y}=−\mathrm{2}−\mathrm{log}_{\mathrm{2}} \mathrm{x} \\ $$$$\frac{\mathrm{x}}{\mathrm{log}_{\mathrm{2}} \mathrm{x}}+\left(−\mathrm{2}−\mathrm{log}_{\mathrm{2}} \mathrm{x}\right)+\mathrm{5}=\mathrm{0} \\ $$$$\frac{\mathrm{x}}{\mathrm{log}_{\mathrm{2}} \mathrm{x}}−\mathrm{log}_{\mathrm{2}} \mathrm{x}+\mathrm{3}=\mathrm{0} \\ $$$$\frac{\mathrm{xlog}_{\mathrm{2}} \mathrm{2}}{\mathrm{log}_{\mathrm{2}} \mathrm{x}}−\mathrm{log}_{\mathrm{2}} \mathrm{x}+\mathrm{3log}_{\mathrm{2}} \mathrm{2}=\mathrm{0} \\ $$$$\frac{\mathrm{log}_{\mathrm{2}} \mathrm{2}^{\mathrm{x}} }{\mathrm{log}_{\mathrm{2}} \mathrm{x}}−\mathrm{log}_{\mathrm{2}} \mathrm{x}+\mathrm{log}_{\mathrm{2}} \mathrm{2}^{\mathrm{3}} =\mathrm{0} \\ $$$$\mathrm{log}_{\mathrm{2}} \left(\mathrm{2}^{\mathrm{x}} \right)^{\mathrm{log}_{\mathrm{2}} \mathrm{x}} −\mathrm{log}_{\mathrm{2}} \mathrm{x}+\mathrm{log}_{\mathrm{2}} \mathrm{2}^{\mathrm{3}} =\mathrm{0} \\ $$$$\mathrm{log}_{\mathrm{2}} \left[\frac{\left(\mathrm{2}^{\mathrm{x}} \right)^{\mathrm{log}_{\mathrm{2}} \mathrm{x}} }{\mathrm{x}}×\mathrm{8}\right]=\mathrm{log}_{\mathrm{2}} \mathrm{1} \\ $$$$\frac{\left(\mathrm{2}^{\mathrm{x}} \right)^{\mathrm{log}_{\mathrm{2}} \mathrm{x}} }{\mathrm{x}}×\mathrm{8}=\mathrm{1} \\ $$$$\mathrm{2}^{\mathrm{3}} ×\left(\mathrm{2}^{\mathrm{x}} \right)^{\mathrm{log}_{\mathrm{2}} \mathrm{x}} =\mathrm{x} \\ $$$$\mathrm{2}^{\mathrm{3}+\mathrm{xlog}_{\mathrm{2}} \mathrm{x}} =\mathrm{x} \\ $$$$\mathrm{log}_{\mathrm{2}} \mathrm{2}^{\mathrm{3}+\mathrm{xlog}_{\mathrm{2}} \mathrm{x}} =\mathrm{log}\:\mathrm{x} \\ $$$$\mathrm{3}+\mathrm{xlog}_{\mathrm{2}} \mathrm{x}=\mathrm{log}_{\mathrm{2}} \:\mathrm{x} \\ $$$$\mathrm{log}_{\mathrm{2}} \:\mathrm{x}−\mathrm{xlog}_{\mathrm{2}} \mathrm{x}=\mathrm{3} \\ $$$$\left(\mathrm{log}_{\mathrm{2}} \mathrm{x}\right)\left(\mathrm{1}−\mathrm{x}\right)=\mathrm{3} \\ $$$$\mathrm{C}^{\mathrm{ontinue}} \\ $$
Commented by prakash jain last updated on 09/May/16
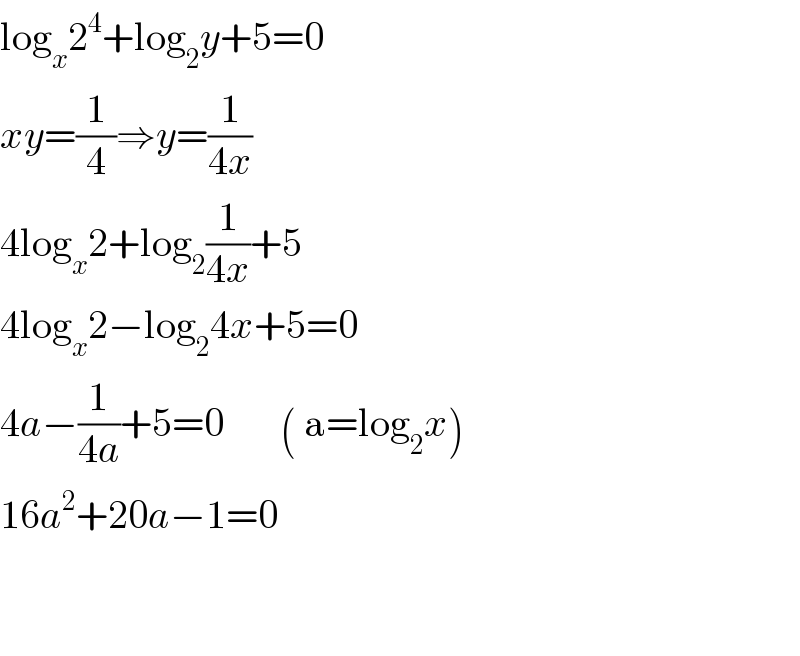
log_x 2^4 +log_2 y+5=0 xy=(1/4)⇒y=(1/(4x)) 4log_x 2+log_2 (1/(4x))+5 4log_x 2−log_2 4x+5=0 4a−(1/(4a))+5=0 ( a=log_2 x) 16a^2 +20a−1=0
$$\mathrm{log}_{{x}} \mathrm{2}^{\mathrm{4}} +\mathrm{log}_{\mathrm{2}} {y}+\mathrm{5}=\mathrm{0} \\ $$$${xy}=\frac{\mathrm{1}}{\mathrm{4}}\Rightarrow{y}=\frac{\mathrm{1}}{\mathrm{4}{x}} \\ $$$$\mathrm{4log}_{{x}} \mathrm{2}+\mathrm{log}_{\mathrm{2}} \frac{\mathrm{1}}{\mathrm{4}{x}}+\mathrm{5} \\ $$$$\mathrm{4log}_{{x}} \mathrm{2}−\mathrm{log}_{\mathrm{2}} \mathrm{4}{x}+\mathrm{5}=\mathrm{0} \\ $$$$\mathrm{4}{a}−\frac{\mathrm{1}}{\mathrm{4}{a}}+\mathrm{5}=\mathrm{0}\:\:\:\:\:\:\:\left(\:\mathrm{a}=\mathrm{log}_{\mathrm{2}} {x}\right) \\ $$$$\mathrm{16}{a}^{\mathrm{2}} +\mathrm{20}{a}−\mathrm{1}=\mathrm{0} \\ $$$$ \\ $$$$ \\ $$
Commented by Rasheed Soomro last updated on 12/May/16
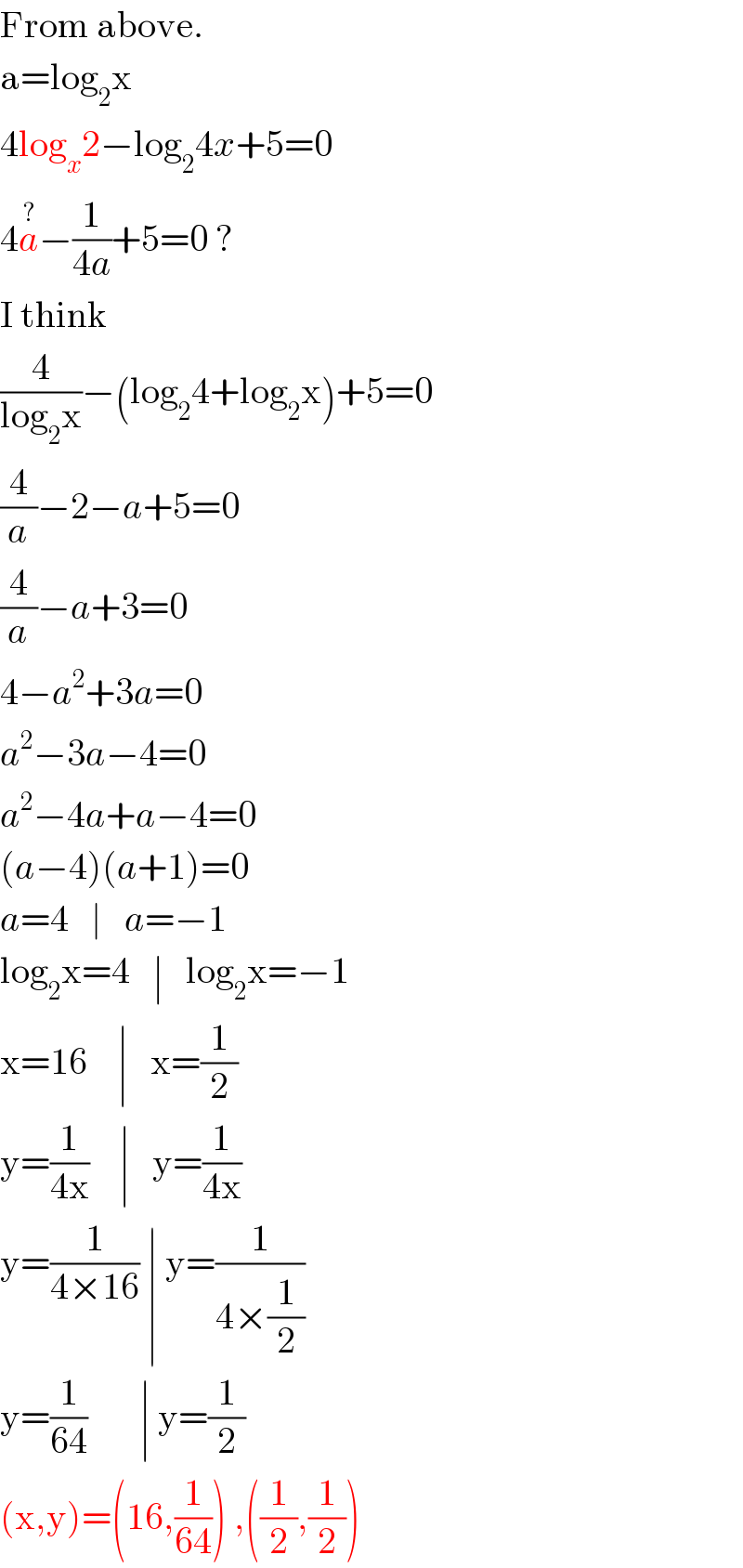
From above. a=log_2 x 4log_x 2−log_2 4x+5=0 4a^(?) −(1/(4a))+5=0 ? I think (4/(log_2 x))−(log_2 4+log_2 x)+5=0 (4/a)−2−a+5=0 (4/a)−a+3=0 4−a^2 +3a=0 a^2 −3a−4=0 a^2 −4a+a−4=0 (a−4)(a+1)=0 a=4 ∣ a=−1 log_2 x=4 ∣ log_2 x=−1 x=16 ∣ x=(1/2) y=(1/(4x)) ∣ y=(1/(4x)) y=(1/(4×16)) ∣ y=(1/(4×(1/2))) y=(1/(64)) ∣ y=(1/2) (x,y)=(16,(1/(64))) ,((1/2),(1/2))
$$\mathrm{From}\:\mathrm{above}. \\ $$$$\mathrm{a}=\mathrm{log}_{\mathrm{2}} \mathrm{x}\: \\ $$$$\mathrm{4log}_{{x}} \mathrm{2}−\mathrm{log}_{\mathrm{2}} \mathrm{4}{x}+\mathrm{5}=\mathrm{0} \\ $$$$\mathrm{4}\overset{?} {{a}}−\frac{\mathrm{1}}{\mathrm{4}{a}}+\mathrm{5}=\mathrm{0}\:? \\ $$$$\mathrm{I}\:\mathrm{think} \\ $$$$\frac{\mathrm{4}}{\mathrm{log}_{\mathrm{2}} \mathrm{x}}−\left(\mathrm{log}_{\mathrm{2}} \mathrm{4}+\mathrm{log}_{\mathrm{2}} \mathrm{x}\right)+\mathrm{5}=\mathrm{0} \\ $$$$\frac{\mathrm{4}}{{a}}−\mathrm{2}−{a}+\mathrm{5}=\mathrm{0} \\ $$$$\frac{\mathrm{4}}{{a}}−{a}+\mathrm{3}=\mathrm{0} \\ $$$$\mathrm{4}−{a}^{\mathrm{2}} +\mathrm{3}{a}=\mathrm{0} \\ $$$${a}^{\mathrm{2}} −\mathrm{3}{a}−\mathrm{4}=\mathrm{0} \\ $$$${a}^{\mathrm{2}} −\mathrm{4}{a}+{a}−\mathrm{4}=\mathrm{0} \\ $$$$\left({a}−\mathrm{4}\right)\left({a}+\mathrm{1}\right)=\mathrm{0} \\ $$$${a}=\mathrm{4}\:\:\:\mid\:\:\:{a}=−\mathrm{1} \\ $$$$\mathrm{log}_{\mathrm{2}} \mathrm{x}=\mathrm{4}\:\:\:\mid\:\:\:\mathrm{log}_{\mathrm{2}} \mathrm{x}=−\mathrm{1} \\ $$$$\mathrm{x}=\mathrm{16}\:\:\:\:\mid\:\:\:\mathrm{x}=\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\mathrm{y}=\frac{\mathrm{1}}{\mathrm{4x}}\:\:\:\:\mid\:\:\:\mathrm{y}=\frac{\mathrm{1}}{\mathrm{4x}} \\ $$$$\mathrm{y}=\frac{\mathrm{1}}{\mathrm{4}×\mathrm{16}}\:\mid\:\mathrm{y}=\frac{\mathrm{1}}{\mathrm{4}×\frac{\mathrm{1}}{\mathrm{2}}} \\ $$$$\mathrm{y}=\frac{\mathrm{1}}{\mathrm{64}}\:\:\:\:\:\:\:\mid\:\mathrm{y}=\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\left(\mathrm{x},\mathrm{y}\right)=\left(\mathrm{16},\frac{\mathrm{1}}{\mathrm{64}}\right)\:,\left(\frac{\mathrm{1}}{\mathrm{2}},\frac{\mathrm{1}}{\mathrm{2}}\right) \\ $$
Commented by prakash jain last updated on 12/May/16
Thanks. Mistake in my solution as you pointed out.
$$\mathrm{Thanks}.\:\mathrm{Mistake}\:\mathrm{in}\:\mathrm{my}\:\mathrm{solution}\:\mathrm{as}\:\mathrm{you}\:\mathrm{pointed} \\ $$$$\mathrm{out}. \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *