Menu Close

Question-5354

Tinku Tara 0 Comments
Pin




Question Number 5354 by Rasheed Soomro last updated on 11/May/16
Commented by Rasheed Soomro last updated on 11/May/16
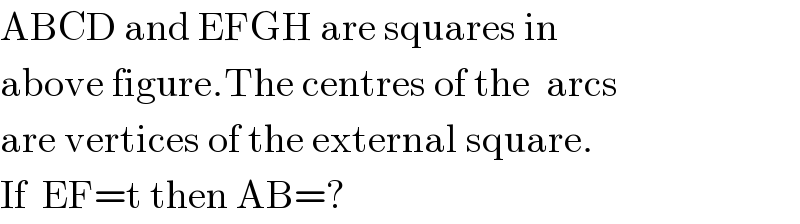
ABCD and EFGH are squares in above figure.The centres of the arcs are vertices of the external square. If EF=t then AB=?
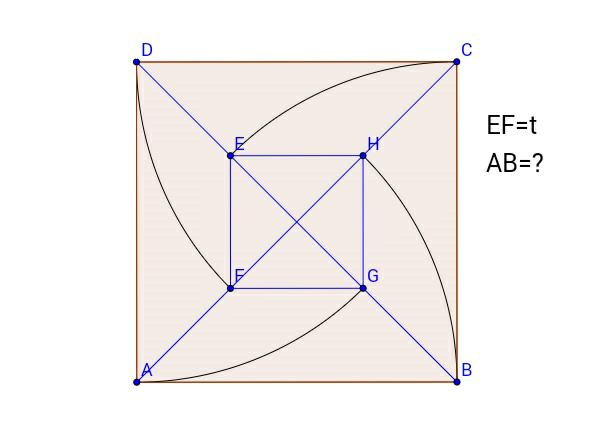
$$\mathrm{ABCD}\:\mathrm{and}\:\mathrm{EFGH}\:\mathrm{are}\:\mathrm{squares}\:\mathrm{in} \\ $$$$\mathrm{above}\:\mathrm{figure}.\mathrm{The}\:\mathrm{centres}\:\mathrm{of}\:\mathrm{the}\:\:\mathrm{arcs}\: \\ $$$$\mathrm{are}\:\mathrm{vertices}\:\mathrm{of}\:\mathrm{the}\:\mathrm{external}\:\mathrm{square}. \\ $$$$\mathrm{If}\:\:\mathrm{EF}=\mathrm{t}\:\mathrm{then}\:\mathrm{AB}=? \\ $$
Commented by Yozzii last updated on 11/May/16
Let sides DA and AB lie on the y and x axes respectively, with A having coordinates (0,0). So let B have coordinates B(r,0) r>0. Since FG=t>0, for EGFH being a square of side t, its sides are parallel to those of □ABCD and its centre coincides with that of □ABCD, then the line x=r/2 reveals a symmetry of the figure. Hence, the x−coordinate of point F is given by x=((r−t)/2). Since F lies on the diagonal AC which coincides with the line y=x, then at F, y=((r−t)/2). So, point F has coordinates (((r−t)/2),((r−t)/2)). Now, the point H is the point F translated t units horizontally and vertically towards the side BC of □ABCD. So, relative to A, H has coordinates (((r−t)/2)+t,((r−t)/2)+t)=(((r+t)/2),((r+t)/2)). But, AH=AB=r since ABH forms a sector of a circle with A as the centre. Therefore, (((r+t)/2)−0)^2 +(((r+t)/2)−0)^2 =r^2 2(((r+t)/2))^2 =r^2 ⇒((r+t)/2)=(r/( (√2)))⇒r+t=r(√2) r((√2)−1)=t⇒r=(t/( (√2)−1))=t(1+(√2)) So, if EF=t⇒AB=t(1+(√2)).
$${Let}\:{sides}\:{DA}\:{and}\:{AB}\:{lie}\:{on}\:{the}\:{y}\:{and}\:{x} \\ $$$${axes}\:{respectively},\:{with}\:{A}\:{having}\: \\ $$$${coordinates}\:\left(\mathrm{0},\mathrm{0}\right).\:{So}\:{let}\:{B}\:{have}\:{coordinates}\:{B}\left({r},\mathrm{0}\right) \\ $$$${r}>\mathrm{0}.\:{Since}\:{FG}={t}>\mathrm{0},\:{for}\:{EGFH}\:{being} \\ $$$${a}\:{square}\:{of}\:{side}\:{t},\:{its}\:{sides}\:{are}\:{parallel} \\ $$$${to}\:{those}\:{of}\:\Box{ABCD}\:{and}\:{its}\:{centre}\: \\ $$$${coincides}\:{with}\:{that}\:{of}\:\Box{ABCD},\:{then} \\ $$$${the}\:{line}\:{x}={r}/\mathrm{2}\:{reveals}\:{a}\:{symmetry} \\ $$$${of}\:{the}\:{figure}.\:{Hence},\:{the}\:{x}−{coordinate} \\ $$$${of}\:{point}\:{F}\:{is}\:{given}\:{by}\:{x}=\frac{{r}−{t}}{\mathrm{2}}.\:{Since}\:{F} \\ $$$${lies}\:{on}\:{the}\:{diagonal}\:{AC}\:{which}\:{coincides} \\ $$$${with}\:{the}\:{line}\:{y}={x},\:{then}\:{at}\:{F},\:{y}=\frac{{r}−{t}}{\mathrm{2}}. \\ $$$${So},\:{point}\:{F}\:{has}\:{coordinates}\:\left(\frac{{r}−{t}}{\mathrm{2}},\frac{{r}−{t}}{\mathrm{2}}\right). \\ $$$${Now},\:{the}\:{point}\:{H}\:{is}\:{the}\:{point}\:{F}\:{translated} \\ $$$${t}\:{units}\:{horizontally}\:{and}\:{vertically}\:{towards} \\ $$$${the}\:{side}\:{BC}\:{of}\:\Box{ABCD}.\:{So},\:{relative}\:{to}\:{A}, \\ $$$${H}\:{has}\:{coordinates}\:\left(\frac{{r}−{t}}{\mathrm{2}}+{t},\frac{{r}−{t}}{\mathrm{2}}+{t}\right)=\left(\frac{{r}+{t}}{\mathrm{2}},\frac{{r}+{t}}{\mathrm{2}}\right). \\ $$$${But},\:{AH}={AB}={r}\:{since}\:{ABH}\:{forms}\:{a}\:{sector}\:{of}\:{a}\:{circle}\:{with}\:{A}\:{as}\:{the}\:{centre}.\:{Therefore}, \\ $$$$\left(\frac{{r}+{t}}{\mathrm{2}}−\mathrm{0}\right)^{\mathrm{2}} +\left(\frac{{r}+{t}}{\mathrm{2}}−\mathrm{0}\right)^{\mathrm{2}} ={r}^{\mathrm{2}} \\ $$$$\mathrm{2}\left(\frac{{r}+{t}}{\mathrm{2}}\right)^{\mathrm{2}} ={r}^{\mathrm{2}} \Rightarrow\frac{{r}+{t}}{\mathrm{2}}=\frac{{r}}{\:\sqrt{\mathrm{2}}}\Rightarrow{r}+{t}={r}\sqrt{\mathrm{2}} \\ $$$${r}\left(\sqrt{\mathrm{2}}−\mathrm{1}\right)={t}\Rightarrow{r}=\frac{{t}}{\:\sqrt{\mathrm{2}}−\mathrm{1}}={t}\left(\mathrm{1}+\sqrt{\mathrm{2}}\right) \\ $$$${So},\:{if}\:{EF}={t}\Rightarrow{AB}={t}\left(\mathrm{1}+\sqrt{\mathrm{2}}\right). \\ $$$$ \\ $$
Commented by Rasheed Soomro last updated on 12/May/16
Good approach!
$$\mathrm{Good}\:\mathrm{approach}! \\ $$
Answered by Rasheed Soomro last updated on 12/May/16
Non-analytical approach. { ((AF+FH=AB)),((CH+FH=CD=AB)) :} { (),() :}AF=CH Let AF=x and Let AB=T ∴CH=x , BC=CD=DA=T since, EF=t So, FG=GH=HE=t FH=(√(t^2 +t^2 ))=(√2) t AF+FH=AB⇒x+(√2) t=T..........................I AC=AF+FH+CH=2x+(√2) t=(√(T^2 +T^2 )) =(√2) T....II 2x+2(√2) t=2T I×2.........III 2x+(√2) t=(√2) T II×1.........IV (√2) t=(2−(√2))T III −IV T=(((√2) t)/(2−(√2)))×((2+(√2))/(2+(√2)))=t((√2)+1)
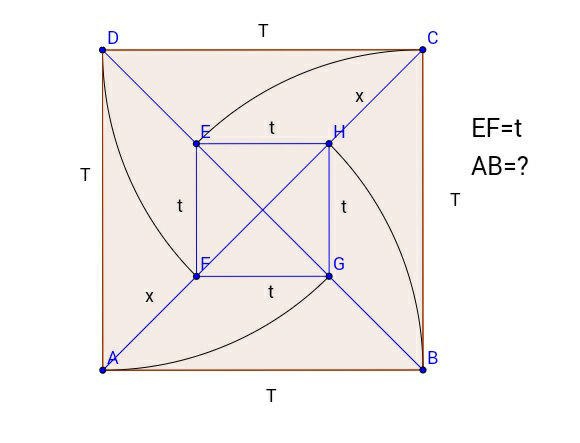
$$\mathrm{Non}-\mathrm{analytical}\:\mathrm{approach}. \\ $$$$\begin{cases}{\mathrm{AF}+\mathrm{FH}=\mathrm{AB}}\\{\mathrm{CH}+\mathrm{FH}=\mathrm{CD}=\mathrm{AB}}\end{cases}\begin{cases}{}\\{}\end{cases}\mathrm{AF}=\mathrm{CH} \\ $$$$\mathrm{Let}\:\mathrm{AF}=\mathrm{x}\:\mathrm{and}\:\mathrm{Let}\:\mathrm{AB}=\mathrm{T} \\ $$$$\therefore\mathrm{CH}=\mathrm{x}\:,\:\mathrm{BC}=\mathrm{CD}=\mathrm{DA}=\mathrm{T} \\ $$$$\mathrm{since}, \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{EF}=\mathrm{t} \\ $$$$\mathrm{So},\:\:\:\:\:\:\:\mathrm{FG}=\mathrm{GH}=\mathrm{HE}=\mathrm{t} \\ $$$$\mathrm{FH}=\sqrt{\mathrm{t}^{\mathrm{2}} +\mathrm{t}^{\mathrm{2}} }=\sqrt{\mathrm{2}}\:\mathrm{t} \\ $$$$\mathrm{AF}+\mathrm{FH}=\mathrm{AB}\Rightarrow\mathrm{x}+\sqrt{\mathrm{2}}\:\mathrm{t}=\mathrm{T}……………………..\mathrm{I} \\ $$$$\mathrm{AC}=\mathrm{AF}+\mathrm{FH}+\mathrm{CH}=\mathrm{2x}+\sqrt{\mathrm{2}}\:\mathrm{t}=\sqrt{\mathrm{T}^{\mathrm{2}} +\mathrm{T}^{\mathrm{2}} }\:=\sqrt{\mathrm{2}}\:\mathrm{T}….\mathrm{II} \\ $$$$\mathrm{2x}+\mathrm{2}\sqrt{\mathrm{2}}\:\mathrm{t}=\mathrm{2T}\:\:\:\:\:\:\mathrm{I}×\mathrm{2}………\mathrm{III} \\ $$$$\mathrm{2x}+\sqrt{\mathrm{2}}\:\mathrm{t}=\sqrt{\mathrm{2}}\:\mathrm{T}\:\:\:\:\:\mathrm{II}×\mathrm{1}………\mathrm{IV} \\ $$$$\sqrt{\mathrm{2}}\:\mathrm{t}=\left(\mathrm{2}−\sqrt{\mathrm{2}}\right)\mathrm{T}\:\:\:\:\:\mathrm{III}\:−\mathrm{IV} \\ $$$$\mathrm{T}=\frac{\sqrt{\mathrm{2}}\:\mathrm{t}}{\mathrm{2}−\sqrt{\mathrm{2}}}×\frac{\mathrm{2}+\sqrt{\mathrm{2}}}{\mathrm{2}+\sqrt{\mathrm{2}}}=\mathrm{t}\left(\sqrt{\mathrm{2}}+\mathrm{1}\right) \\ $$
Commented by Yozzii last updated on 12/May/16
Nice! My understanding of and confidence in Euclidean geometry still needs some work. The education system I′ve gone through placed emphasis on analytical methods.
$${Nice}!\:{My}\:{understanding}\:{of}\:{and}\:{confidence}\:{in}\:{Euclidean}\:{geometry}\:{still} \\ $$$${needs}\:{some}\:{work}.\:{The}\:{education}\:{system}\:{I}'{ve}\:{gone}\:{through} \\ $$$${placed}\:{emphasis}\:{on}\:{analytical}\:{methods}.\: \\ $$$$ \\ $$
Commented by Rasheed Soomro last updated on 12/May/16
Commented by Rasheed Soomro last updated on 12/May/16
I have been observing you since your joining to this forum.Your logic is very powerful, so Euclidean geometry is simple for you! ..... Have you qualified the cambridge exam/test?
$$\mathrm{I}\:\mathrm{have}\:\mathrm{been}\:\mathrm{observing}\:\mathrm{you}\:\mathrm{since}\:\mathrm{your}\:\mathrm{joining} \\ $$$$\mathrm{to}\:\mathrm{this}\:\mathrm{forum}.\mathrm{Your}\:\mathrm{logic}\:\mathrm{is}\:\mathrm{very}\:\mathrm{powerful},\:\mathrm{so} \\ $$$$\mathrm{Euclidean}\:\mathrm{geometry}\:\mathrm{is}\:\mathrm{simple}\:\mathrm{for}\:\mathrm{you}! \\ $$$$….. \\ $$$$\:\mathrm{Have}\:\mathrm{you}\:\mathrm{qualified}\:\mathrm{the}\:\mathrm{cambridge}\:\mathrm{exam}/\mathrm{test}? \\ $$
Commented by Yozzii last updated on 13/May/16
I′ve only sat the CIE Further Math A Level exam in 2015, and that doesn′t have an emphasis on Euclidean geometry. It appears a bit in studying mechanics, but at that level rigorous proof writing isn′t required. That′s the past. Now I′m just helping myself grow in mathematical skill, rigour and presentation before I begin undergraduate university studies from September 2016 in mathematics.
$${I}'{ve}\:{only}\:{sat}\:{the}\:{CIE}\:{Further}\:{Math} \\ $$$${A}\:{Level}\:{exam}\:{in}\:\mathrm{2015},\:{and}\:{that}\:{doesn}'{t} \\ $$$${have}\:{an}\:{emphasis}\:{on}\:{Euclidean}\:{geometry}. \\ $$$${It}\:{appears}\:{a}\:{bit}\:{in}\:{studying}\:{mechanics}, \\ $$$${but}\:{at}\:{that}\:{level}\:{rigorous}\:{proof}\:{writing} \\ $$$${isn}'{t}\:{required}.\:{That}'{s}\:{the}\:{past}. \\ $$$${Now}\:{I}'{m}\:{just}\:{helping}\:{myself}\:{grow}\: \\ $$$${in}\:{mathematical}\:{skill},\:{rigour}\:{and}\:{presentation} \\ $$$${before}\:{I}\:{begin}\:{undergraduate}\:{university}\:{studies} \\ $$$${from}\:{September}\:\mathrm{2016}\:{in}\:{mathematics}. \\ $$$$ \\ $$
Commented by Rasheed Soomro last updated on 13/May/16
Th𝛂nkS ! Actually, I didn′t consider any connection between your exam and Eucledean geometry. I only wanted to be informed about your progress.
$$\mathbb{T}\boldsymbol{\mathrm{h}\alpha\mathrm{n}}\Bbbk\mathcal{S}\:!\:\mathrm{Actually},\:\mathrm{I}\:\mathrm{didn}'\mathrm{t}\:\mathrm{consider}\:\mathrm{any}\:\mathrm{connection} \\ $$$$\mathrm{between}\:\mathrm{your}\:\mathrm{exam}\:\mathrm{and}\:\mathrm{Eucledean}\:\mathrm{geometry}. \\ $$$$\mathrm{I}\:\mathrm{only}\:\mathrm{wanted}\:\mathrm{to}\:\mathrm{be}\:\mathrm{informed}\:\mathrm{about}\:\mathrm{your} \\ $$$$\mathrm{progress}. \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *