Question Number 5705 by sanusihammed last updated on 24/May/16
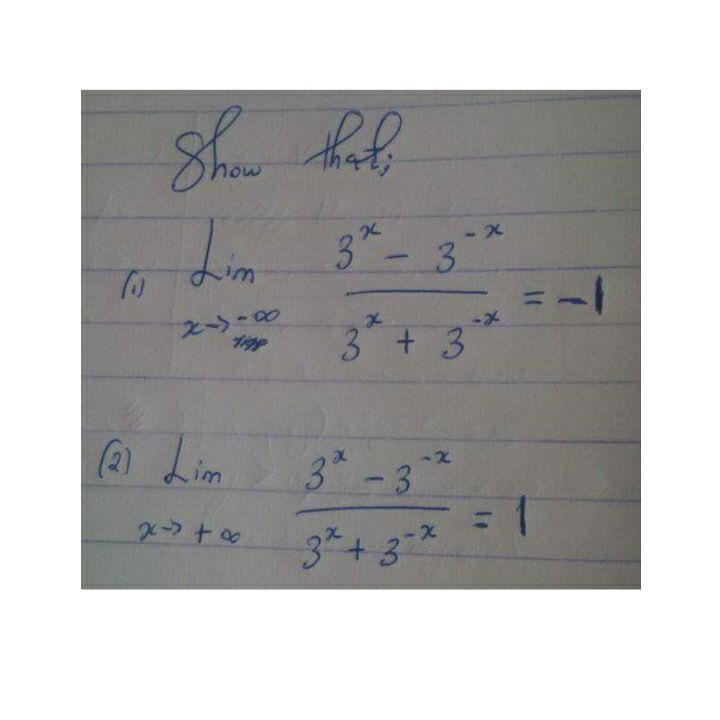
Answered by FilupSmith last updated on 24/May/16
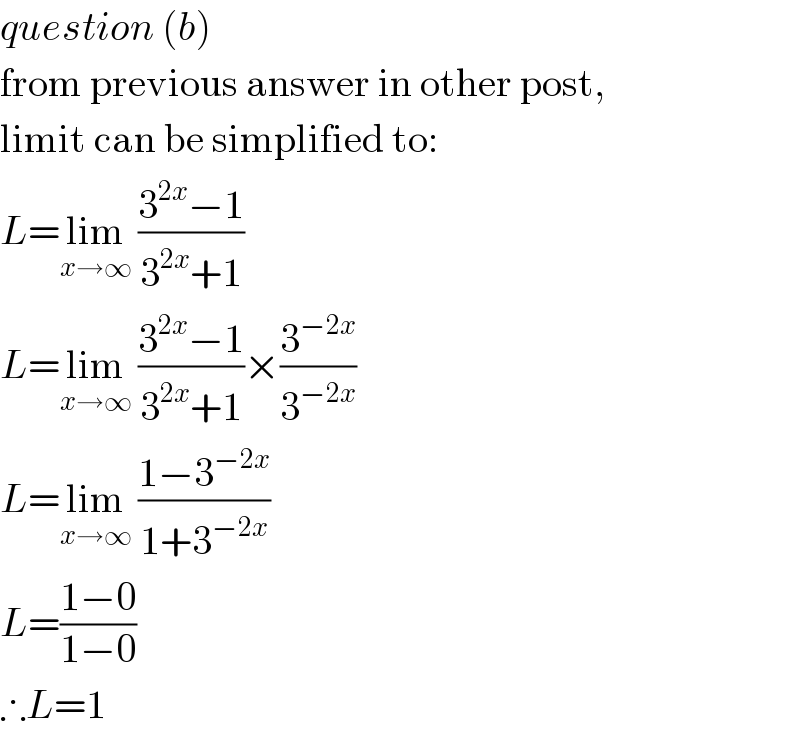
$${question}\:\left({b}\right) \\ $$$$\mathrm{from}\:\mathrm{previous}\:\mathrm{answer}\:\mathrm{in}\:\mathrm{other}\:\mathrm{post}, \\ $$$$\mathrm{limit}\:\mathrm{can}\:\mathrm{be}\:\mathrm{simplified}\:\mathrm{to}: \\ $$$${L}=\underset{{x}\rightarrow\infty} {\mathrm{lim}}\:\frac{\mathrm{3}^{\mathrm{2}{x}} −\mathrm{1}}{\mathrm{3}^{\mathrm{2}{x}} +\mathrm{1}} \\ $$$${L}=\underset{{x}\rightarrow\infty} {\mathrm{lim}}\:\frac{\mathrm{3}^{\mathrm{2}{x}} −\mathrm{1}}{\mathrm{3}^{\mathrm{2}{x}} +\mathrm{1}}×\frac{\mathrm{3}^{−\mathrm{2}{x}} }{\mathrm{3}^{−\mathrm{2}{x}} } \\ $$$${L}=\underset{{x}\rightarrow\infty} {\mathrm{lim}}\:\frac{\mathrm{1}−\mathrm{3}^{−\mathrm{2}{x}} }{\mathrm{1}+\mathrm{3}^{−\mathrm{2}{x}} } \\ $$$${L}=\frac{\mathrm{1}−\mathrm{0}}{\mathrm{1}−\mathrm{0}} \\ $$$$\therefore{L}=\mathrm{1} \\ $$
Commented by sanusihammed last updated on 24/May/16

$${Thanks}\:{so}\:{much}. \\ $$
