Question Number 5809 by Apoorva last updated on 28/May/16
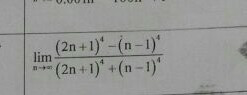
Commented by Apoorva last updated on 28/May/16
$${please}\:{solve}\:{this}\:{limit} \\ $$
Answered by Yozzii last updated on 28/May/16
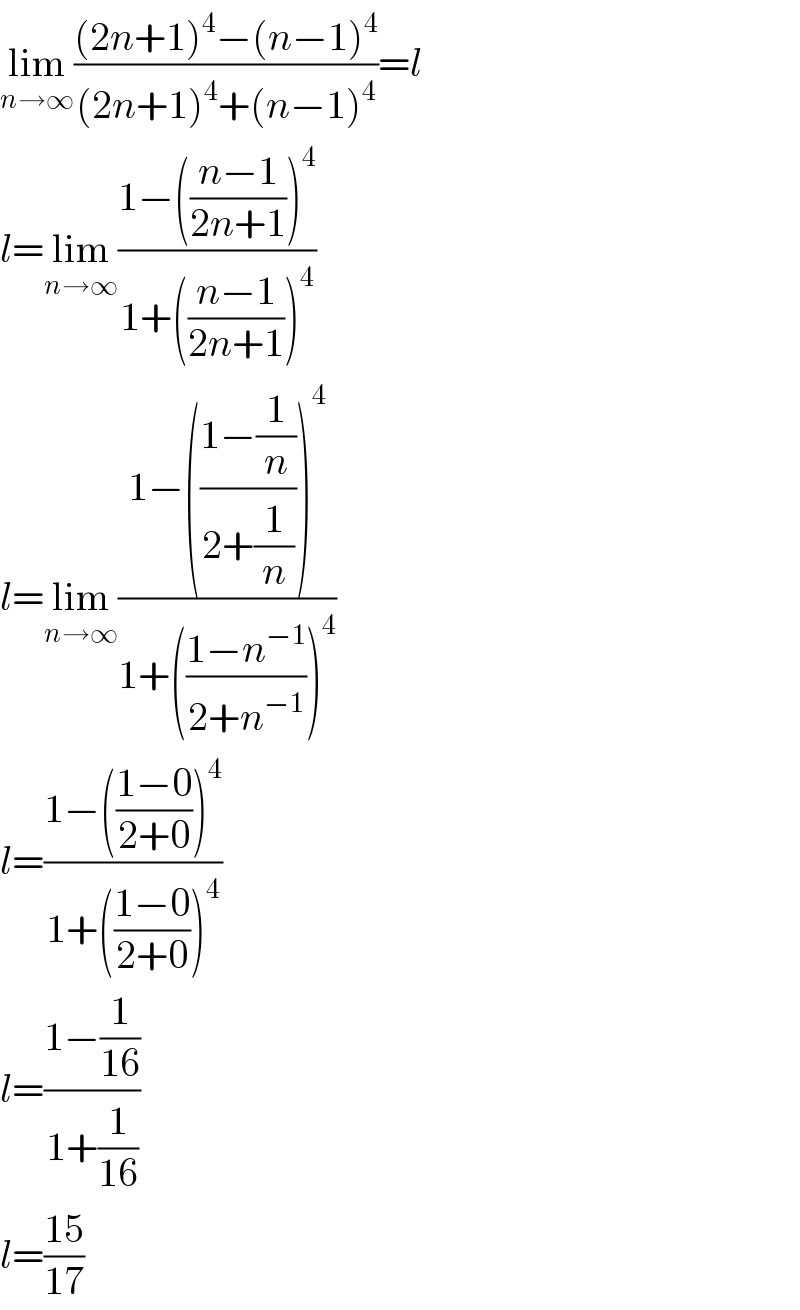
$$\underset{{n}\rightarrow\infty} {\mathrm{lim}}\frac{\left(\mathrm{2}{n}+\mathrm{1}\right)^{\mathrm{4}} −\left({n}−\mathrm{1}\right)^{\mathrm{4}} }{\left(\mathrm{2}{n}+\mathrm{1}\right)^{\mathrm{4}} +\left({n}−\mathrm{1}\right)^{\mathrm{4}} }={l}\: \\ $$$${l}=\underset{{n}\rightarrow\infty} {\mathrm{lim}}\frac{\mathrm{1}−\left(\frac{{n}−\mathrm{1}}{\mathrm{2}{n}+\mathrm{1}}\right)^{\mathrm{4}} }{\mathrm{1}+\left(\frac{{n}−\mathrm{1}}{\mathrm{2}{n}+\mathrm{1}}\right)^{\mathrm{4}} } \\ $$$${l}=\underset{{n}\rightarrow\infty} {\mathrm{lim}}\frac{\mathrm{1}−\left(\frac{\mathrm{1}−\frac{\mathrm{1}}{{n}}}{\mathrm{2}+\frac{\mathrm{1}}{{n}}}\right)^{\mathrm{4}} }{\mathrm{1}+\left(\frac{\mathrm{1}−{n}^{−\mathrm{1}} }{\mathrm{2}+{n}^{−\mathrm{1}} }\right)^{\mathrm{4}} } \\ $$$${l}=\frac{\mathrm{1}−\left(\frac{\mathrm{1}−\mathrm{0}}{\mathrm{2}+\mathrm{0}}\right)^{\mathrm{4}} }{\mathrm{1}+\left(\frac{\mathrm{1}−\mathrm{0}}{\mathrm{2}+\mathrm{0}}\right)^{\mathrm{4}} } \\ $$$${l}=\frac{\mathrm{1}−\frac{\mathrm{1}}{\mathrm{16}}}{\mathrm{1}+\frac{\mathrm{1}}{\mathrm{16}}} \\ $$$${l}=\frac{\mathrm{15}}{\mathrm{17}} \\ $$
Commented by Apoorva last updated on 29/May/16

$${Thankyou} \\ $$
