Menu Close

Question-5825

Tinku Tara 0 Comments
Pin




Question Number 5825 by Rasheed Soomro last updated on 30/May/16
Commented by Rasheed Soomro last updated on 30/May/16
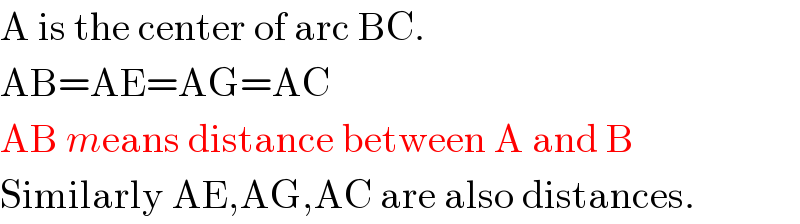
A is the center of arc BC. AB=AE=AG=AC AB means distance between A and B Similarly AE,AG,AC are also distances.
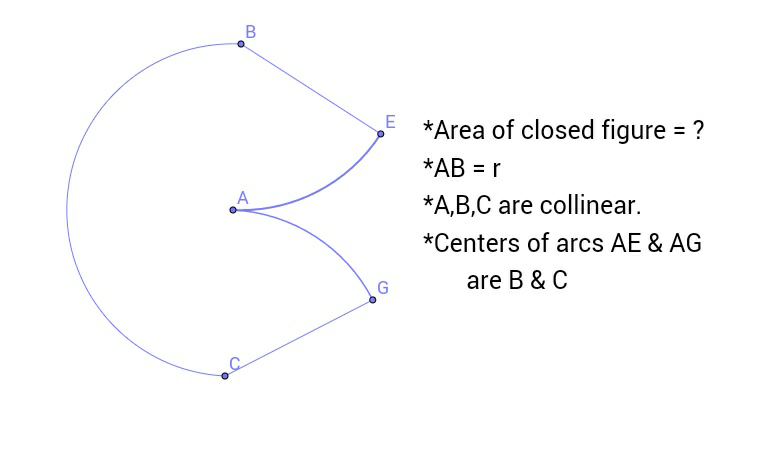
$$\mathrm{A}\:\mathrm{is}\:\mathrm{the}\:\mathrm{center}\:\mathrm{of}\:\mathrm{arc}\:\mathrm{BC}. \\ $$$$\mathrm{AB}=\mathrm{AE}=\mathrm{AG}=\mathrm{AC} \\ $$$$\mathrm{AB}\:{m}\mathrm{eans}\:\mathrm{distance}\:\mathrm{between}\:\mathrm{A}\:\mathrm{and}\:\mathrm{B} \\ $$$$\mathrm{Similarly}\:\mathrm{AE},\mathrm{AG},\mathrm{AC}\:\mathrm{are}\:\mathrm{also}\:\mathrm{distances}. \\ $$
Answered by Yozzii last updated on 30/May/16
The centre of the arc AE is B and ∣AB∣=∣AE∣>0. Since AE is an arc ⇒∣AB∣=∣BE∣ and ∣AE∣=∣AB∣θ where θ=∠ABE. ∴ θ=((∣AE∣)/(∣AB∣))=1 rad. C is the centre of the arc AG and ∣AG∣=∣AC∣. We similarly find ∠ACG=α=1 rad. We are given that A,B & C are collinear points. So ∠BAC=γ=π rad. A is the centre of the arc BC. We now employ the formula for the area of the sectors whose angles are θ,α and γ respectively. A_θ =(1/2)(∣AB∣)^2 θ=(((AB)^2 )/2) A_α =(1/2)(∣AC∣)^2 α=(((∣AC∣)^2 )/2)=(((∣AB∣)^2 )/2) ∵ ∣AB∣=∣AC∣ A_γ =(1/2)(∣AB∣)^2 γ=(((∣AB∣)^2 )/2)π. The total area of the closed figure is then A=A_γ +A_θ +A_α or A=(((∣AB∣)^2 )/2)(2+π)=(r^2 /2)(2+π) ∵∣AB∣=r.
$${The}\:{centre}\:{of}\:{the}\:{arc}\:{AE}\:{is}\:{B}\:{and}\: \\ $$$$\mid{AB}\mid=\mid{AE}\mid>\mathrm{0}.\:{Since}\:{AE}\:{is}\:{an}\:{arc} \\ $$$$\Rightarrow\mid{AB}\mid=\mid{BE}\mid\:{and}\:\mid{AE}\mid=\mid{AB}\mid\theta\: \\ $$$${where}\:\theta=\angle{ABE}.\:\therefore\:\theta=\frac{\mid{AE}\mid}{\mid{AB}\mid}=\mathrm{1}\:{rad}. \\ $$$${C}\:{is}\:{the}\:{centre}\:{of}\:{the}\:{arc}\:{AG}\:{and} \\ $$$$\mid{AG}\mid=\mid{AC}\mid.\:{We}\:{similarly}\:{find}\:\angle{ACG}=\alpha=\mathrm{1}\:{rad}. \\ $$$${We}\:{are}\:{given}\:{that}\:{A},{B}\:\&\:{C}\:{are}\: \\ $$$${collinear}\:{points}.\:{So}\:\angle{BAC}=\gamma=\pi\:{rad}. \\ $$$${A}\:{is}\:{the}\:{centre}\:{of}\:{the}\:{arc}\:{BC}. \\ $$$${We}\:{now}\:{employ}\:{the}\:{formula}\:{for} \\ $$$${the}\:{area}\:{of}\:{the}\:{sectors}\:{whose}\:{angles} \\ $$$${are}\:\theta,\alpha\:{and}\:\gamma\:{respectively}. \\ $$$${A}_{\theta} =\frac{\mathrm{1}}{\mathrm{2}}\left(\mid{AB}\mid\right)^{\mathrm{2}} \theta=\frac{\left({AB}\right)^{\mathrm{2}} }{\mathrm{2}} \\ $$$${A}_{\alpha} =\frac{\mathrm{1}}{\mathrm{2}}\left(\mid{AC}\mid\right)^{\mathrm{2}} \alpha=\frac{\left(\mid{AC}\mid\right)^{\mathrm{2}} }{\mathrm{2}}=\frac{\left(\mid{AB}\mid\right)^{\mathrm{2}} }{\mathrm{2}}\:\:\:\because\:\mid{AB}\mid=\mid{AC}\mid \\ $$$${A}_{\gamma} =\frac{\mathrm{1}}{\mathrm{2}}\left(\mid{AB}\mid\right)^{\mathrm{2}} \gamma=\frac{\left(\mid{AB}\mid\right)^{\mathrm{2}} }{\mathrm{2}}\pi. \\ $$$${The}\:{total}\:{area}\:{of}\:{the}\:{closed}\:{figure} \\ $$$${is}\:{then}\:{A}={A}_{\gamma} +{A}_{\theta} +{A}_{\alpha} \:\:{or} \\ $$$${A}=\frac{\left(\mid{AB}\mid\right)^{\mathrm{2}} }{\mathrm{2}}\left(\mathrm{2}+\pi\right)=\frac{{r}^{\mathrm{2}} }{\mathrm{2}}\left(\mathrm{2}+\pi\right)\:\:\:\:\because\mid{AB}\mid={r}. \\ $$
Commented by Rasheed Soomro last updated on 30/May/16
Very sorry that my question was not clear. According to your understanding you are very right! But I didn′t mean that. By AE ,AB,AG,...I meant distances between points. Where I meant arc I wrote arc AG etc.
$$\mathrm{Very}\:\mathrm{sorry}\:\mathrm{that}\:\mathrm{my}\:\mathrm{question}\:\mathrm{was}\:\mathrm{not}\:\mathrm{clear}. \\ $$$$\mathrm{According}\:\mathrm{to}\:\mathrm{your}\:\mathrm{understanding}\:\mathrm{you}\:\mathrm{are} \\ $$$$\mathrm{very}\:\mathrm{right}! \\ $$$$\mathrm{But}\:\mathrm{I}\:\mathrm{didn}'\mathrm{t}\:\mathrm{mean}\:\mathrm{that}. \\ $$$$\mathrm{By}\:\mathrm{AE}\:,\mathrm{AB},\mathrm{AG},…\mathrm{I}\:\mathrm{meant}\:\mathrm{distances}\:\mathrm{between} \\ $$$$\mathrm{points}.\:\mathrm{Where}\:\mathrm{I}\:\mathrm{meant}\:\mathrm{arc}\:\mathrm{I}\:\mathrm{wrote}\:\mathrm{arc}\:\mathrm{AG}\:{etc}. \\ $$
Commented by Yozzii last updated on 30/May/16
My calculation considers the symbolism you used initially as measures of distances between points. If you′d like, we can write for example the distance between points A and B as ∣AB∣.
$${My}\:{calculation}\:{considers}\:{the}\:{symbolism} \\ $$$${you}\:{used}\:{initially}\:{as}\:{measures}\:{of} \\ $$$${distances}\:{between}\:{points}.\:{If}\:{you}'{d} \\ $$$${like},\:{we}\:{can}\:{write}\:{for}\:{example}\:{the}\:{distance} \\ $$$${between}\:{points}\:{A}\:{and}\:{B}\:{as}\:\mid{AB}\mid. \\ $$$$ \\ $$
Commented by Rasheed Soomro last updated on 07/Jun/16
!SknaHT_(←)
$$\underset{\leftarrow} {!\mathcal{S}{kna}\mathcal{HT}} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *