Question Number 6056 by Rasheed Soomro last updated on 11/Jun/16
Commented by Rasheed Soomro last updated on 11/Jun/16
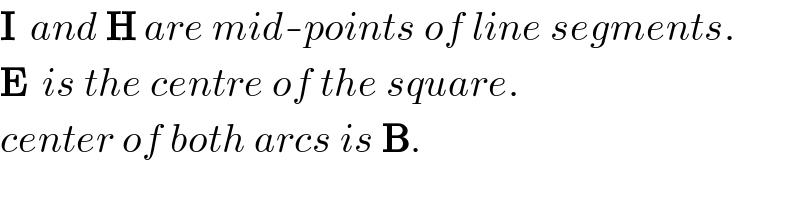
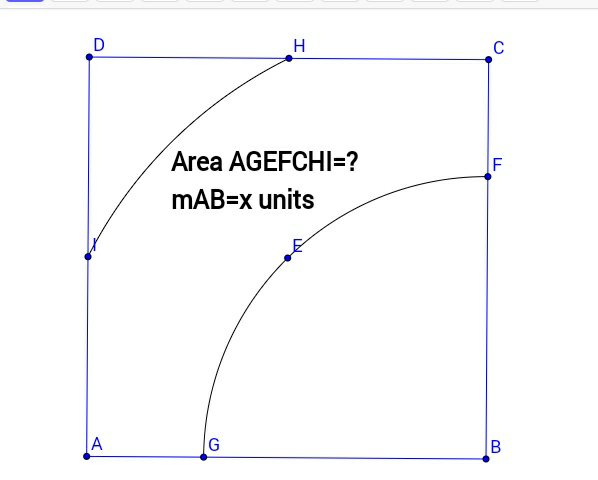
$$\boldsymbol{\mathrm{I}}\:\:{and}\:\boldsymbol{\mathrm{H}}\:{are}\:{mid}-{points}\:{of}\:{line}\:{segments}. \\ $$$$\boldsymbol{\mathrm{E}}\:\:{is}\:{the}\:{centre}\:{of}\:{the}\:{square}. \\ $$$${center}\:{of}\:{both}\:{arcs}\:{is}\:\boldsymbol{\mathrm{B}}. \\ $$
Commented by Yozzii last updated on 11/Jun/16
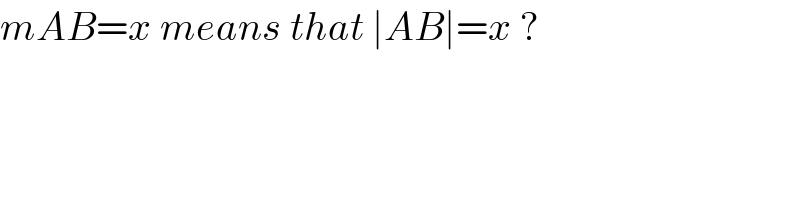
$${mAB}={x}\:{means}\:{that}\:\mid{AB}\mid={x}\:? \\ $$
Commented by Rasheed Soomro last updated on 11/Jun/16

$${Yes}. \\ $$
Answered by Yozzii last updated on 11/Jun/16

$$\Box{ABCD},\:{H}\:{lies}\:{on}\:{DC},\:{F}\:{lies}\:{on}\:{BC}, \\ $$$${G}\:{lies}\:{on}\:{AB},\:{I}\:{lies}\:{on}\:{AD},\:{E}\:{lies} \\ $$$${on}\:{arc}\:{GF},\:{E}\:{is}\:{the}\:{centre}\:{of}\:\Box{ABCD}, \\ $$$${HI}\:{is}\:{an}\:{arc},\:{centre}\:{of}\:{both}\:{arcs}\:{is}\:{B}, \\ $$$$\mid{HD}\mid=\mathrm{0}.\mathrm{5}\mid{DC}\mid,\:\mid{AI}\mid=\mathrm{0}.\mathrm{5}\mid{AD}\mid, \\ $$$$\mid{AB}\mid={x}>\mathrm{0},\:{area}\:{of}\:{AGEFCHI}=? \\ $$$$−−−−−−−−−−−−−−−−−−−−−−−−−− \\ $$$${Note}\:{that}\:\mid{AB}\mid=\mid{BC}\mid=\mid{CD}\mid=\mid{DA}\mid={x}>\mathrm{0}. \\ $$$${By}\:{the}\:{Phythagorean}\:{theorem},\: \\ $$$$\mid{EB}\mid=\sqrt{\left(\frac{\mid{AB}\mid}{\mathrm{2}}\right)^{\mathrm{2}} +\left(\frac{\mid{BC}\mid}{\mathrm{2}}\right)^{\mathrm{2}} }=\sqrt{\frac{{x}^{\mathrm{2}} }{\mathrm{4}}×\mathrm{2}}={x}\frac{\sqrt{\mathrm{2}}}{\mathrm{2}} \\ $$$$\angle{ABC}=\frac{\pi}{\mathrm{2}}.\:{Let}\:{the}\:{area}\:{of}\:{the}\:{sector}\:{FEGB} \\ $$$${be}\:{denoted}\:{by}\:{A}.\:\therefore\:{A}=\frac{\mathrm{1}}{\mathrm{2}}{r}^{\mathrm{2}} \theta \\ $$$${A}=\frac{\mathrm{1}}{\mathrm{2}}\mid{EB}\mid^{\mathrm{2}} \left(\angle{ABC}\right)=\frac{\mathrm{1}}{\mathrm{2}}\left(\frac{{x}^{\mathrm{2}} }{\mathrm{2}}\right)\frac{\pi}{\mathrm{2}}=\frac{\pi{x}^{\mathrm{2}} }{\mathrm{8}}\:{units}^{\mathrm{2}} . \\ $$$$ \\ $$$${For}\:\bigtriangleup{HCB},\:{its}\:{area}\:{is}\:{given}\:{by} \\ $$$${A}_{\mathrm{1}} =\frac{\mathrm{1}}{\mathrm{2}}\mid{BC}\mid\mid{CH}\mid=\frac{\mathrm{1}}{\mathrm{2}}{x}×\frac{\mathrm{1}}{\mathrm{2}}{x}=\frac{{x}^{\mathrm{2}} }{\mathrm{4}}\:{units}^{\mathrm{2}} . \\ $$$${By}\:{symmetry}\:{of}\:{the}\:{figure},\:{for}\:\bigtriangleup{IAB} \\ $$$${its}\:{area}\:{is}\:{also}\:{A}_{\mathrm{1}} =\frac{{x}^{\mathrm{2}} }{\mathrm{4}}\:{units}^{\mathrm{2}} . \\ $$$${Now},\:{in}\:\bigtriangleup{BCH},\:{tan}\angle{HBC}=\frac{\mid{HC}\mid}{\mid{BC}\mid}=\frac{{x}/\mathrm{2}}{{x}}=\frac{\mathrm{1}}{\mathrm{2}} \\ $$$${Since}\:\mathrm{0}<\angle{HBC}<\frac{\pi}{\mathrm{2}}\Rightarrow\angle{HBC}={tan}^{−\mathrm{1}} \mathrm{0}.\mathrm{5}. \\ $$$${Also},\:\angle{IBA}={tan}^{−\mathrm{1}} \mathrm{0}.\mathrm{5}. \\ $$$${Thus},\:\angle{IBH}=\frac{\pi}{\mathrm{2}}−\left(\angle{IBA}+\angle{HBC}\right) \\ $$$$\angle{IBH}=\frac{\pi}{\mathrm{2}}−\mathrm{2}{tan}^{−\mathrm{1}} \mathrm{0}.\mathrm{5}. \\ $$$${Now},\:\mid{HB}\mid^{\mathrm{2}} =\mid{IB}\mid^{\mathrm{2}} =\mid{HC}\mid^{\mathrm{2}} +\mid{BC}\mid^{\mathrm{2}} \:{by}\: \\ $$$${the}\:{Phythagorean}\:{theorem}. \\ $$$$\therefore\mid{HB}\mid^{\mathrm{2}} =\frac{{x}^{\mathrm{2}} }{\mathrm{4}}+{x}^{\mathrm{2}} =\frac{\mathrm{5}{x}^{\mathrm{2}} }{\mathrm{4}}. \\ $$$${Thus},\:{the}\:{area}\:{of}\:{the}\:{sector}\:{IHB}\:{is} \\ $$$${given}\:{by}\:{A}_{\mathrm{2}} =\frac{\mathrm{1}}{\mathrm{2}}\mid{HB}\mid^{\mathrm{2}} \left(\angle{IBH}\right) \\ $$$${or}\:{A}_{\mathrm{2}} =\frac{\mathrm{1}}{\mathrm{2}}\left(\frac{\mathrm{5}{x}^{\mathrm{2}} }{\mathrm{4}}\right)\left(\frac{\pi}{\mathrm{2}}−\mathrm{2}{tan}^{−\mathrm{1}} \mathrm{0}.\mathrm{5}\right) \\ $$$${A}_{\mathrm{2}} =\frac{\mathrm{5}{x}^{\mathrm{2}} \left(\pi−\mathrm{4}{tan}^{−\mathrm{1}} \mathrm{0}.\mathrm{5}\right)}{\mathrm{16}}\:{units}^{\mathrm{2}} . \\ $$$${The}\:{area}\:{of}\:{the}\:{region}\:{AGBFCHI}\:{is} \\ $$$${given}\:{by}\:{A}_{\mathrm{3}} ={A}_{\mathrm{2}} +\mathrm{2}{A}_{\mathrm{1}} \\ $$$${A}_{\mathrm{3}} =\frac{\mathrm{5}{x}^{\mathrm{2}} \left(\pi−\mathrm{4}{tan}^{−\mathrm{1}} \mathrm{0}.\mathrm{5}\right)}{\mathrm{16}}+\mathrm{2}×\frac{{x}^{\mathrm{2}} }{\mathrm{4}} \\ $$$${A}_{\mathrm{3}} =\frac{{x}^{\mathrm{2}} }{\mathrm{2}}\left(\frac{\mathrm{5}\pi−\mathrm{20}{tan}^{−\mathrm{1}} \mathrm{0}.\mathrm{5}+\mathrm{16}}{\mathrm{16}}\right) \\ $$$${A}_{\mathrm{3}} =\frac{{x}^{\mathrm{2}} \left(\mathrm{5}\pi+\mathrm{16}−\mathrm{20}{tan}^{−\mathrm{1}} \mathrm{0}.\mathrm{5}\right)}{\mathrm{32}} \\ $$$${The}\:{final}\:{answer}\:{is}\:{given}\:{by}\: \\ $$$${A}_{\mathrm{3}} −{A}={x}^{\mathrm{2}} \left(\frac{\mathrm{5}\pi+\mathrm{16}−\mathrm{20}{tan}^{−\mathrm{1}} \mathrm{0}.\mathrm{5}}{\mathrm{32}}−\frac{\pi}{\mathrm{8}}\right) \\ $$$${A}_{\mathrm{3}} −{A}={x}^{\mathrm{2}} \left(\frac{\pi+\mathrm{16}−\mathrm{20}{tan}^{−\mathrm{1}} \mathrm{0}.\mathrm{5}}{\mathrm{32}}\right)\:{units}^{\mathrm{2}} \\ $$
Commented by Rasheed Soomro last updated on 11/Jun/16

$$\overset{\mathcal{V}} {\mathcal{G}_{\mathcal{OO}} \mathcal{D}}\:\:\mathcal{S}\mathfrak{t}{rategy}! \\ $$$$\mathcal{A}\:\mathcal{S}\mathfrak{t}{rategy}\:\mathcal{I}\:{didn}'{t}\:{think}\:{of}! \\ $$
