Question Number 6202 by sanusihammed last updated on 18/Jun/16

Commented by Rasheed Soomro last updated on 18/Jun/16

$${What}\:{is}\:{meant}\:{by}\:\:'\:{persegi}\:'?\:{Square}? \\ $$
Answered by Rasheed Soomro last updated on 23/Jun/16
![In △ABC, ∣BC∣=(√(∣AC∣^2 +∣AB∣^2 )) =(√(2^2 +12^2 ))=(√(148))=2(√(37)) ∵ BCED is a square ∴ ∣BC∣=∣CE∣=∣ED∣=∣BD∣=2(√(37)) and the diagonal ∣BE∣=∣CD∣=(√((2(√(37)))^2 +(2(√(37)))^2 )) =(√(2×4×37))=2(√(74)) The half diagonal ∣CF∣=∣BF∣=∣DF∣=∣EF∣=(√(74)) tan (m∠ACB)=((∣AB∣)/(∣AC∣))=((12)/2)=6 m∠ACB=tan^(−1) 6≈80.5377° In △ACF, m∠ACF=45°+tan^(−1) 6≈125.5377° ∣AC∣=2 and ∣CF∣=(√(74)) ∣AF∣^2 =∣AC∣^2 +∣CF∣^2 −2∣AC∣∣CF∣cos (m∠ACF) [Cosine law] ∣AF∣=(√((2)^2 +((√(74)))^2 −2(2)((√(74)))cos (125.5377°))) =9.899 ((∣AC∣)/(sin(m∠ CFA)))=((∣AF∣)/(sin(m∠ ACF))) [Sine law] (2/(sin(m∠ CFA) ))=((9.899)/(sin(125.5377°) )) sin(m∠ CFA)=((2sin(125.5377°))/(9.899))≈0.1644 m∠ CFA=sin^(−1) (0.1644)=9.462 In △CGF, m∠GCF=45° [Angle between side and diagonal of square] ∣CF∣=(√(74)) m∠CFG(=m∠CFA)=9.462 m∠CGF=180°−45°−9.462°=125.538° Using sine law ((∣GF∣)/(sin 45°)) = ((∣CF∣)/(sin(125.538°))) ∣GF∣= ((∣CF∣ sin(45))/(sin(125.538°)))=(((√(74)) sin 45)/(sin(125.538°))) So, ∣GF∣= 7.475](https://www.tinkutara.com/question/Q6212.png)
$${In}\:\bigtriangleup{ABC},\:\:\:\mid{BC}\mid=\sqrt{\mid{AC}\mid^{\mathrm{2}} +\mid{AB}\mid^{\mathrm{2}} } \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\sqrt{\mathrm{2}^{\mathrm{2}} +\mathrm{12}^{\mathrm{2}} }=\sqrt{\mathrm{148}}=\mathrm{2}\sqrt{\mathrm{37}} \\ $$$$\because\:{BCED}\:{is}\:{a}\:{square} \\ $$$$\therefore\:\mid{BC}\mid=\mid{CE}\mid=\mid{ED}\mid=\mid{BD}\mid=\mathrm{2}\sqrt{\mathrm{37}} \\ $$$${and}\:{the}\:{diagonal} \\ $$$$\:\:\:\:\:\:\mid{BE}\mid=\mid{CD}\mid=\sqrt{\left(\mathrm{2}\sqrt{\mathrm{37}}\right)^{\mathrm{2}} +\left(\mathrm{2}\sqrt{\mathrm{37}}\right)^{\mathrm{2}} } \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\sqrt{\mathrm{2}×\mathrm{4}×\mathrm{37}}=\mathrm{2}\sqrt{\mathrm{74}} \\ $$$${The}\:{half}\:{diagonal} \\ $$$$\:\:\:\:\:\:\mid{CF}\mid=\mid{BF}\mid=\mid{DF}\mid=\mid{EF}\mid=\sqrt{\mathrm{74}} \\ $$$$\mathrm{tan}\:\left({m}\angle{ACB}\right)=\frac{\mid{AB}\mid}{\mid{AC}\mid}=\frac{\mathrm{12}}{\mathrm{2}}=\mathrm{6} \\ $$$$\:\:\:\:{m}\angle{ACB}=\mathrm{tan}^{−\mathrm{1}} \mathrm{6}\approx\mathrm{80}.\mathrm{5377}° \\ $$$$ \\ $$$${In}\:\bigtriangleup{ACF},\:\:{m}\angle{ACF}=\mathrm{45}°+\mathrm{tan}^{−\mathrm{1}} \mathrm{6}\approx\mathrm{125}.\mathrm{5377}° \\ $$$$\:\:\:\:\:\:\:\:\:\:\mid{AC}\mid=\mathrm{2}\:\:\:\:{and}\:\:\:\:\mid{CF}\mid=\sqrt{\mathrm{74}} \\ $$$$\mid{AF}\mid^{\mathrm{2}} =\mid{AC}\mid^{\mathrm{2}} +\mid{CF}\mid^{\mathrm{2}} −\mathrm{2}\mid{AC}\mid\mid{CF}\mid\mathrm{cos}\:\left({m}\angle{ACF}\right)\:\left[{Cosine}\:{law}\right] \\ $$$$\mid{AF}\mid=\sqrt{\left(\mathrm{2}\right)^{\mathrm{2}} +\left(\sqrt{\mathrm{74}}\right)^{\mathrm{2}} −\mathrm{2}\left(\mathrm{2}\right)\left(\sqrt{\mathrm{74}}\right)\mathrm{cos}\:\left(\mathrm{125}.\mathrm{5377}°\right)} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:=\mathrm{9}.\mathrm{899} \\ $$$$\frac{\mid{AC}\mid}{\mathrm{sin}\left({m}\angle\:{CFA}\right)}=\frac{\mid{AF}\mid}{\mathrm{sin}\left({m}\angle\:{ACF}\right)}\:\:\:\:\:\:\left[{Sine}\:{law}\right] \\ $$$$\frac{\mathrm{2}}{\mathrm{sin}\left({m}\angle\:{CFA}\right)\:}=\frac{\mathrm{9}.\mathrm{899}}{\mathrm{sin}\left(\mathrm{125}.\mathrm{5377}°\right)\:} \\ $$$$\mathrm{sin}\left({m}\angle\:{CFA}\right)=\frac{\mathrm{2sin}\left(\mathrm{125}.\mathrm{5377}°\right)}{\mathrm{9}.\mathrm{899}}\approx\mathrm{0}.\mathrm{1644} \\ $$$${m}\angle\:{CFA}=\mathrm{sin}^{−\mathrm{1}} \left(\mathrm{0}.\mathrm{1644}\right)=\mathrm{9}.\mathrm{462} \\ $$$$ \\ $$$${In}\:\bigtriangleup{CGF},\:\:{m}\angle{GCF}=\mathrm{45}°\:\left[{Angle}\:{between}\:{side}\:{and}\:{diagonal}\:{of}\:{square}\right] \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mid{CF}\mid=\sqrt{\mathrm{74}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{m}\angle{CFG}\left(={m}\angle{CFA}\right)=\mathrm{9}.\mathrm{462} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{m}\angle{CGF}=\mathrm{180}°−\mathrm{45}°−\mathrm{9}.\mathrm{462}°=\mathrm{125}.\mathrm{538}° \\ $$$${Using}\:{sine}\:{law} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\frac{\mid{GF}\mid}{\mathrm{sin}\:\mathrm{45}°}\:=\:\:\frac{\mid{CF}\mid}{\mathrm{sin}\left(\mathrm{125}.\mathrm{538}°\right)} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mid{GF}\mid=\:\:\frac{\mid{CF}\mid\:\mathrm{sin}\left(\mathrm{45}\right)}{\mathrm{sin}\left(\mathrm{125}.\mathrm{538}°\right)}=\frac{\sqrt{\mathrm{74}}\:\mathrm{sin}\:\mathrm{45}}{\mathrm{sin}\left(\mathrm{125}.\mathrm{538}°\right)} \\ $$$${So},\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mid{GF}\mid=\:\mathrm{7}.\mathrm{475} \\ $$$$ \\ $$
Commented by sanusihammed last updated on 18/Jun/16

$${Thanks}\:{so}\:{much} \\ $$
Commented by sandy_suhendra last updated on 22/Jun/16
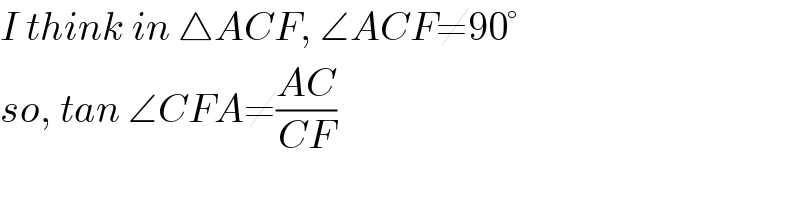
$${I}\:{think}\:{in}\:\bigtriangleup{ACF},\:\angle{ACF}\neq\mathrm{90}°\: \\ $$$${so},\:{tan}\:\angle{CFA}\neq\frac{{AC}}{{CF}} \\ $$
Commented by Rasheed Soomro last updated on 23/Jun/16
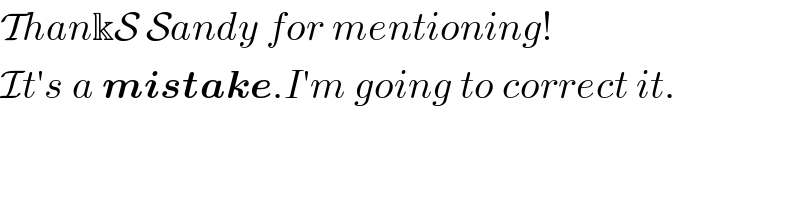
$$\mathcal{T}{han}\Bbbk\mathcal{S}\:\mathcal{S}{andy}\:{for}\:{mentioning}! \\ $$$$\mathcal{I}{t}'{s}\:{a}\:\boldsymbol{{mistake}}.{I}'{m}\:{going}\:{to}\:{correct}\:{it}. \\ $$
Commented by Rasheed Soomro last updated on 23/Jun/16
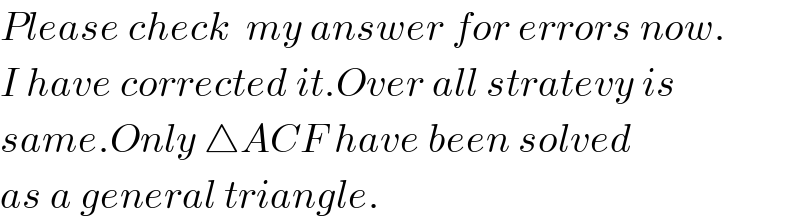
$${Please}\:{check}\:\:{my}\:{answer}\:{for}\:{errors}\:{now}. \\ $$$${I}\:{have}\:{corrected}\:{it}.{Over}\:{all}\:{stratevy}\:{is} \\ $$$${same}.{Only}\:\bigtriangleup{ACF}\:{have}\:{been}\:{solved} \\ $$$${as}\:{a}\:{general}\:{triangle}. \\ $$
Commented by sandy_suhendra last updated on 25/Jun/16
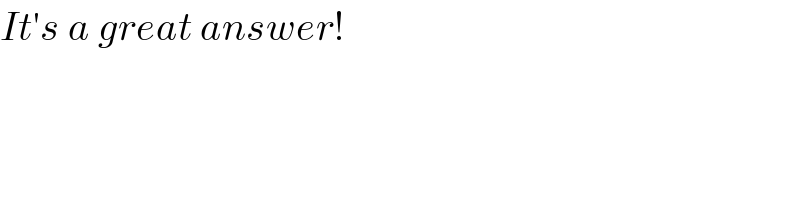
$${It}'{s}\:{a}\:{great}\:{answer}! \\ $$
