Question Number 6203 by sanusihammed last updated on 18/Jun/16
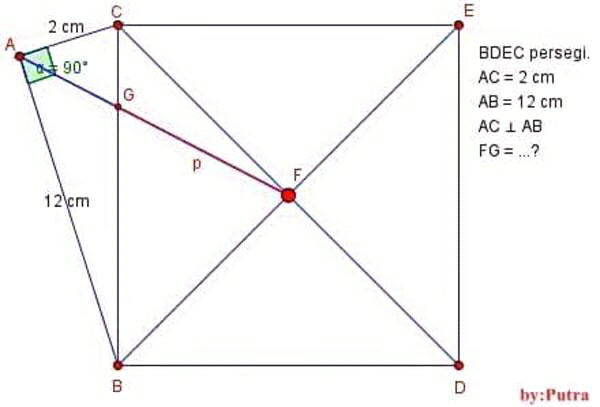
Answered by nburiburu last updated on 25/Jun/16

$${defining} \\ $$$${AC}={a} \\ $$$${AB}={b} \\ $$$${then} \\ $$$${BC}=\sqrt{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} }={c} \\ $$$${since}\:{BCED}\:{square} \\ $$$${CF}={FB}=\frac{{c}}{\:\sqrt{\mathrm{2}}}\:=\sqrt{\frac{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} }{\mathrm{2}}} \\ $$$${Now}\:{to}\:{find}\:{AF}={x}\:{I}\:{need}\:{the}\:{height}\:{of}\:{C}\overset{\bigtriangleup} {{A}B}\:{and}\:{C}\overset{\bigtriangleup} {{F}B}. \\ $$$${so}\:{I}\:{need} \\ $$$${M}=\:{midpoint}\left\{{CB}\right\} \\ $$$${N}=\:{Proy}_{{CB}} ^{\bot} \left({A}\right) \\ $$$${AN}\:={i} \\ $$$${by}\:{triangles}\:{similarities}:\:{B}\overset{\bigtriangleup} {{A}C}\:\approx\:{A}\overset{\bigtriangleup} {{N}C} \\ $$$$\frac{{i}}{{b}}=\frac{{a}}{{c}}\:\Rightarrow\:{i}=\frac{{ab}}{{c}}=\frac{{ab}}{\:\sqrt{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} }} \\ $$$${MB}={MF}={j}\:=\frac{{c}}{\mathrm{2}}=\frac{\sqrt{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} }}{\mathrm{2}} \\ $$$${and}\:{seeing}\:{the}\:{triangles}\:{F}\overset{\bigtriangleup} {{M}G}\:{and}\:{A}\overset{\bigtriangleup} {{N}G}\:{I}\:{can}\:{think}\:{a}\:{new}\:{right}\:{triangle}\:{with}\:{x}\:{as}\:{hypothenuse},\:{catet}\:{MF}+{AN}\:{and}\:{MN} \\ $$$${MN}=\:{k}={BC}−{CN}−{MB}={c}−{i}−{j} \\ $$$${k}=\:\sqrt{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} }−\frac{{ab}}{\:\sqrt{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} }}−\frac{\sqrt{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} }}{\mathrm{2}}=\frac{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} −\mathrm{2}{ab}}{\mathrm{2}\sqrt{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} }}=\frac{\left({b}−{a}\right)^{\mathrm{2}} }{\mathrm{2}\sqrt{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} }} \\ $$$${by}\:{Pithagoras}\:{theorem} \\ $$$${AF}^{\mathrm{2}} =\left({MF}+{AN}\right)^{\mathrm{2}} +{MN}^{\mathrm{2}} \\ $$$${x}=\:\sqrt{\left({j}+{i}\right)^{\mathrm{2}} +{k}^{\mathrm{2}} }\:=\sqrt{\left(\frac{\sqrt{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} }}{\mathrm{2}}+\frac{{ab}}{\:\sqrt{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} }}\right)^{\mathrm{2}} +\left(\frac{\left({b}−{a}\right)^{\mathrm{2}} }{\mathrm{2}\sqrt{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} }}\right)^{\mathrm{2}} } \\ $$$${x}=\sqrt{\left(\frac{\left({a}+{b}\right)^{\mathrm{2}} }{\mathrm{2}\sqrt{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} }}\right)^{\mathrm{2}} +\left(\frac{\left({b}−{a}\right)^{\mathrm{2}} }{\mathrm{2}\sqrt{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} }}\right)^{\mathrm{2}} } \\ $$$${and}\:{now}\:{it}\:{is}\:{simple}. \\ $$$$ \\ $$
Commented by Rasheed Soomro last updated on 25/Jun/16

$${A}\:{deep}\:{approach}!\:{Used}\:{only}\:{right}-{angled} \\ $$$${trigonometry}!\:{Only}\:{pythagorean}\:{theorm}! \\ $$$${Appreciation}! \\ $$$${But}\:{you}\:{have}\:{determined}\:\mid{AF}\mid\:{whereas}\:\mid{FG}\mid \\ $$$${is}\:{required}. \\ $$
Commented by nburiburu last updated on 25/Jun/16

$${FG}\:{is}\:{simplier}\:{to}\:{find}\:{with}\:{the}\bigtriangleup{FMG}\approx\bigtriangleup{made}\:{with}\:{x}\:{as}\:{hypotenuse} \\ $$$${Some}\:{work}\:{has}\:{to}\:{be}\:{done}\:{by}\:{the}\:{student},{haha}. \\ $$$${My}\:{main}\:{idea}\:{is}\:{to}\:{show}\:{that}\:{trigonometry}\:{wasn}'{t}\:{necessary}\:{per}\:{se}… \\ $$$$ \\ $$$$ \\ $$
Commented by Rasheed Soomro last updated on 25/Jun/16

$${Ok}\:{sir}!\:\:{The}\:{student}\:{will}\:{try}\:{to}\:{meet}\:{your}\: \\ $$$${expectations}! \\ $$$${One}\:{request}:\:{Please}\:{do}\:{not}\:{write}\:{toooooo}\:{long}\: \\ $$$${lines}. \\ $$
