Question Number 6217 by Rasheed Soomro last updated on 18/Jun/16
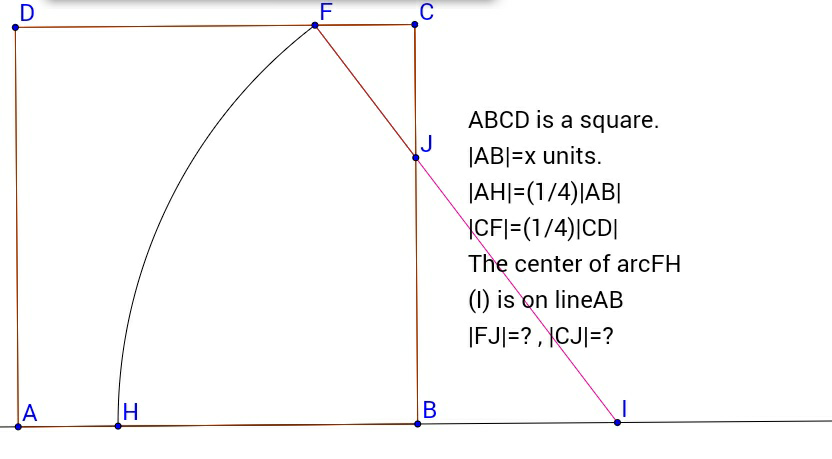
Commented by Rasheed Soomro last updated on 22/Jun/16

$$\mid{FJ}\mid=? \\ $$
Commented by sandy_suhendra last updated on 22/Jun/16
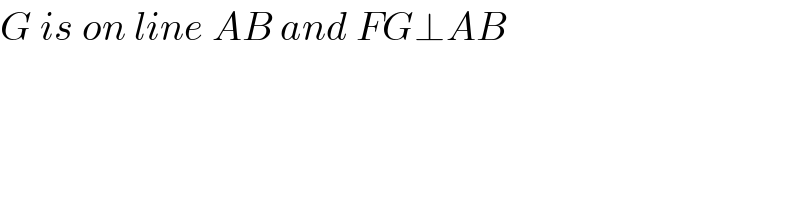
$${G}\:{is}\:{on}\:{line}\:{AB}\:{and}\:{FG}\bot{AB} \\ $$
Answered by sandy_suhendra last updated on 22/Jun/16
![BI=a →HI=FI=(3/4)x+a FC=GB=(1/4)x → GI=(1/4)x+a FG^2 +GI^2 =FI^2 ⇔ x^2 +((1/4)x+a)^2 =((3/4)x+a)^2 ⇔ x^2 +(1/(16))x^2 +(1/2)ax+a^2 =(9/(16))x^2 +1(1/2)ax+a^2 ⇔ (1/2)x^2 =ax ⇔ a=(1/2)x △FCJ∼△JBI → ((CJ)/(JB))= ((FJ)/(JI))=((FC)/(BI))=(((1/4)x)/((1/2)x))=(1/2) CJ=(1/3)CB=(1/3)x FJ=(1/3)FI=(1/3)[(3/4)x+(1/2)x]=(5/(12))x](https://www.tinkutara.com/question/Q6306.png)
$${BI}={a}\:\rightarrow{HI}={FI}=\frac{\mathrm{3}}{\mathrm{4}}{x}+{a} \\ $$$${FC}={GB}=\frac{\mathrm{1}}{\mathrm{4}}{x}\:\rightarrow\:{GI}=\frac{\mathrm{1}}{\mathrm{4}}{x}+{a} \\ $$$${FG}^{\mathrm{2}} +{GI}^{\mathrm{2}} ={FI}^{\mathrm{2}} \\ $$$$\Leftrightarrow\:{x}^{\mathrm{2}} +\left(\frac{\mathrm{1}}{\mathrm{4}}{x}+{a}\right)^{\mathrm{2}} =\left(\frac{\mathrm{3}}{\mathrm{4}}{x}+{a}\right)^{\mathrm{2}} \\ $$$$\Leftrightarrow\:{x}^{\mathrm{2}} +\frac{\mathrm{1}}{\mathrm{16}}{x}^{\mathrm{2}} +\frac{\mathrm{1}}{\mathrm{2}}{ax}+{a}^{\mathrm{2}} =\frac{\mathrm{9}}{\mathrm{16}}{x}^{\mathrm{2}} +\mathrm{1}\frac{\mathrm{1}}{\mathrm{2}}{ax}+{a}^{\mathrm{2}} \\ $$$$\Leftrightarrow\:\frac{\mathrm{1}}{\mathrm{2}}{x}^{\mathrm{2}} ={ax} \\ $$$$\Leftrightarrow\:{a}=\frac{\mathrm{1}}{\mathrm{2}}{x} \\ $$$$\bigtriangleup{FCJ}\sim\bigtriangleup{JBI}\:\rightarrow\:\frac{{CJ}}{{JB}}=\:\frac{{FJ}}{{JI}}=\frac{{FC}}{{BI}}=\frac{\frac{\mathrm{1}}{\mathrm{4}}{x}}{\frac{\mathrm{1}}{\mathrm{2}}{x}}=\frac{\mathrm{1}}{\mathrm{2}} \\ $$$${CJ}=\frac{\mathrm{1}}{\mathrm{3}}{CB}=\frac{\mathrm{1}}{\mathrm{3}}{x} \\ $$$${FJ}=\frac{\mathrm{1}}{\mathrm{3}}{FI}=\frac{\mathrm{1}}{\mathrm{3}}\left[\frac{\mathrm{3}}{\mathrm{4}}{x}+\frac{\mathrm{1}}{\mathrm{2}}{x}\right]=\frac{\mathrm{5}}{\mathrm{12}}{x} \\ $$
Commented by Rasheed Soomro last updated on 23/Jun/16

$$\mathcal{NICE}! \\ $$$$\mathcal{E}{ven}\:{better}\:{if}\:{reasoning}\:{for}\:\bigtriangleup{FCJ}\sim\bigtriangleup{JBI} \\ $$$${be}\:{included}\:\left({for}\:{perfectness}\:{only}\right). \\ $$
