Menu Close

Question-6289

Tinku Tara 0 Comments
Pin




Question Number 6289 by sanusihammed last updated on 22/Jun/16
Commented by FilupSmith last updated on 22/Jun/16
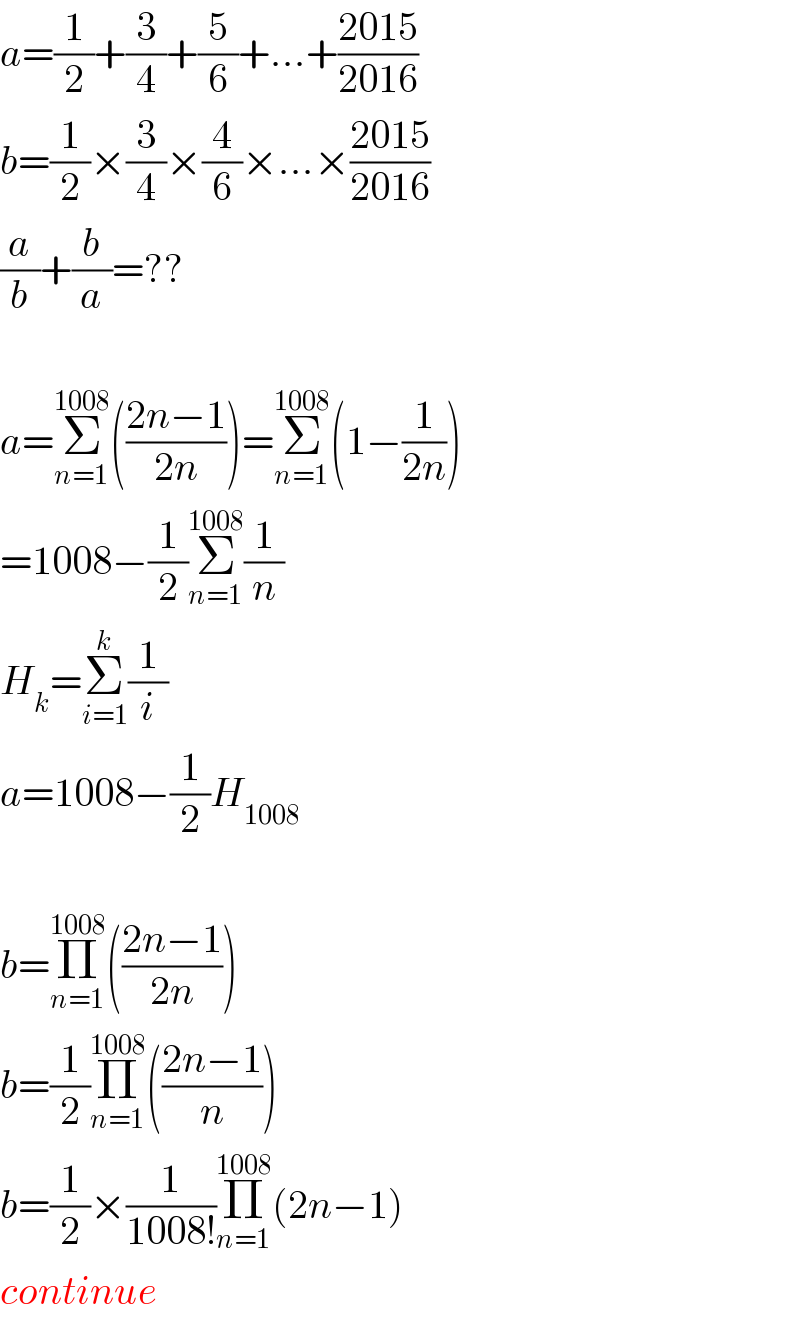
a=(1/2)+(3/4)+(5/6)+...+((2015)/(2016)) b=(1/2)×(3/4)×(4/6)×...×((2015)/(2016)) (a/b)+(b/a)=?? a=Σ_(n=1) ^(1008) (((2n−1)/(2n)))=Σ_(n=1) ^(1008) (1−(1/(2n))) =1008−(1/2)Σ_(n=1) ^(1008) (1/n) H_k =Σ_(i=1) ^k (1/i) a=1008−(1/2)H_(1008) b=Π_(n=1) ^(1008) (((2n−1)/(2n))) b=(1/2)Π_(n=1) ^(1008) (((2n−1)/n)) b=(1/2)×(1/(1008!))Π_(n=1) ^(1008) (2n−1) continue
$${a}=\frac{\mathrm{1}}{\mathrm{2}}+\frac{\mathrm{3}}{\mathrm{4}}+\frac{\mathrm{5}}{\mathrm{6}}+…+\frac{\mathrm{2015}}{\mathrm{2016}} \\ $$$${b}=\frac{\mathrm{1}}{\mathrm{2}}×\frac{\mathrm{3}}{\mathrm{4}}×\frac{\mathrm{4}}{\mathrm{6}}×…×\frac{\mathrm{2015}}{\mathrm{2016}} \\ $$$$\frac{{a}}{{b}}+\frac{{b}}{{a}}=?? \\ $$$$ \\ $$$${a}=\underset{{n}=\mathrm{1}} {\overset{\mathrm{1008}} {\sum}}\left(\frac{\mathrm{2}{n}−\mathrm{1}}{\mathrm{2}{n}}\right)=\underset{{n}=\mathrm{1}} {\overset{\mathrm{1008}} {\sum}}\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}{n}}\right) \\ $$$$=\mathrm{1008}−\frac{\mathrm{1}}{\mathrm{2}}\underset{{n}=\mathrm{1}} {\overset{\mathrm{1008}} {\sum}}\frac{\mathrm{1}}{{n}} \\ $$$${H}_{{k}} =\underset{{i}=\mathrm{1}} {\overset{{k}} {\sum}}\frac{\mathrm{1}}{{i}} \\ $$$${a}=\mathrm{1008}−\frac{\mathrm{1}}{\mathrm{2}}{H}_{\mathrm{1008}} \\ $$$$ \\ $$$${b}=\underset{{n}=\mathrm{1}} {\overset{\mathrm{1008}} {\prod}}\left(\frac{\mathrm{2}{n}−\mathrm{1}}{\mathrm{2}{n}}\right) \\ $$$${b}=\frac{\mathrm{1}}{\mathrm{2}}\underset{{n}=\mathrm{1}} {\overset{\mathrm{1008}} {\prod}}\left(\frac{\mathrm{2}{n}−\mathrm{1}}{{n}}\right) \\ $$$${b}=\frac{\mathrm{1}}{\mathrm{2}}×\frac{\mathrm{1}}{\mathrm{1008}!}\underset{{n}=\mathrm{1}} {\overset{\mathrm{1008}} {\prod}}\left(\mathrm{2}{n}−\mathrm{1}\right) \\ $$$${continue} \\ $$
Commented by Rasheed Soomro last updated on 22/Jun/16
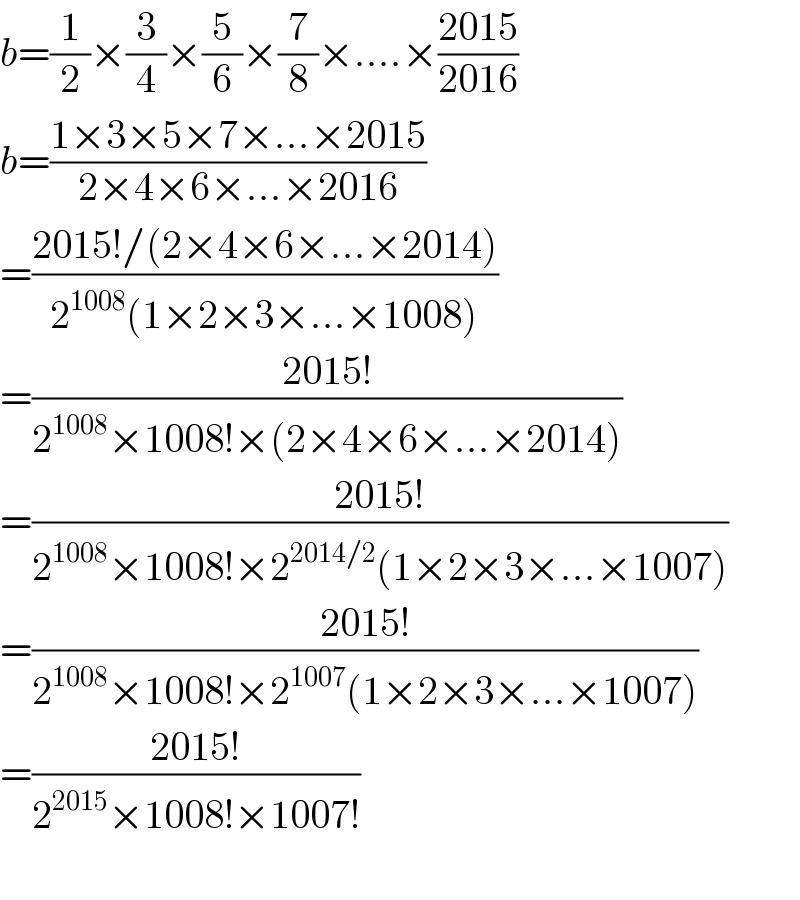
b=(1/2)×(3/4)×(5/6)×(7/8)×....×((2015)/(2016)) b=((1×3×5×7×...×2015)/(2×4×6×...×2016)) =((2015!/(2×4×6×...×2014))/(2^(1008) (1×2×3×...×1008))) =((2015!)/(2^(1008) ×1008!×(2×4×6×...×2014))) =((2015!)/(2^(1008) ×1008!×2^(2014/2) (1×2×3×...×1007))) =((2015!)/(2^(1008) ×1008!×2^(1007) (1×2×3×...×1007))) =((2015!)/(2^(2015) ×1008!×1007!))
$${b}=\frac{\mathrm{1}}{\mathrm{2}}×\frac{\mathrm{3}}{\mathrm{4}}×\frac{\mathrm{5}}{\mathrm{6}}×\frac{\mathrm{7}}{\mathrm{8}}×….×\frac{\mathrm{2015}}{\mathrm{2016}} \\ $$$${b}=\frac{\mathrm{1}×\mathrm{3}×\mathrm{5}×\mathrm{7}×…×\mathrm{2015}}{\mathrm{2}×\mathrm{4}×\mathrm{6}×…×\mathrm{2016}} \\ $$$$=\frac{\mathrm{2015}!/\left(\mathrm{2}×\mathrm{4}×\mathrm{6}×…×\mathrm{2014}\right)}{\mathrm{2}^{\mathrm{1008}} \left(\mathrm{1}×\mathrm{2}×\mathrm{3}×…×\mathrm{1008}\right)} \\ $$$$=\frac{\mathrm{2015}!}{\mathrm{2}^{\mathrm{1008}} ×\mathrm{1008}!×\left(\mathrm{2}×\mathrm{4}×\mathrm{6}×…×\mathrm{2014}\right)} \\ $$$$=\frac{\mathrm{2015}!}{\mathrm{2}^{\mathrm{1008}} ×\mathrm{1008}!×\mathrm{2}^{\mathrm{2014}/\mathrm{2}} \left(\mathrm{1}×\mathrm{2}×\mathrm{3}×…×\mathrm{1007}\right)} \\ $$$$=\frac{\mathrm{2015}!}{\mathrm{2}^{\mathrm{1008}} ×\mathrm{1008}!×\mathrm{2}^{\mathrm{1007}} \left(\mathrm{1}×\mathrm{2}×\mathrm{3}×…×\mathrm{1007}\right)} \\ $$$$=\frac{\mathrm{2015}!}{\mathrm{2}^{\mathrm{2015}} ×\mathrm{1008}!×\mathrm{1007}!} \\ $$$$ \\ $$
Commented by Yozzii last updated on 22/Jun/16
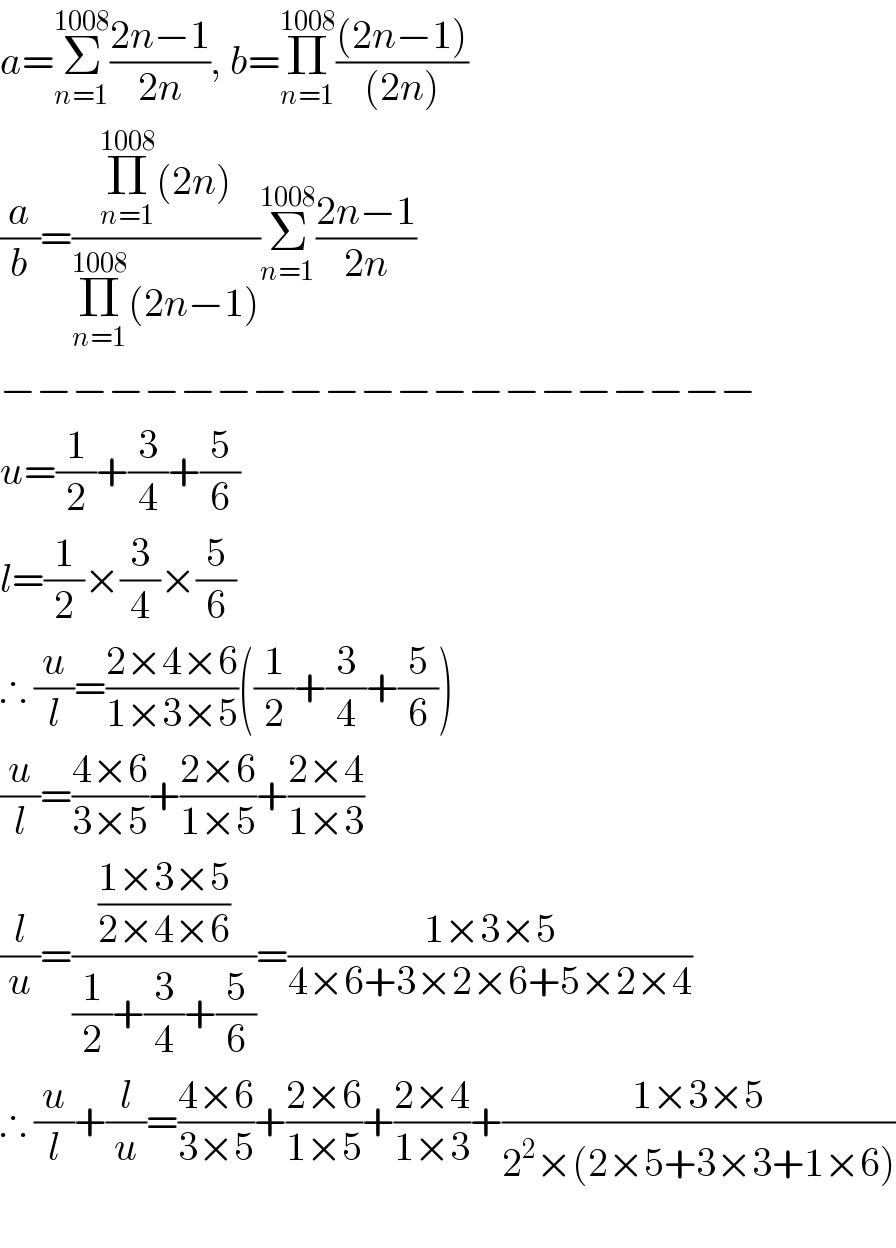
a=Σ_(n=1) ^(1008) ((2n−1)/(2n)), b=Π_(n=1) ^(1008) (((2n−1))/((2n))) (a/b)=((Π_(n=1) ^(1008) (2n))/(Π_(n=1) ^(1008) (2n−1)))Σ_(n=1) ^(1008) ((2n−1)/(2n)) −−−−−−−−−−−−−−−−−−−−− u=(1/2)+(3/4)+(5/6) l=(1/2)×(3/4)×(5/6) ∴ (u/l)=((2×4×6)/(1×3×5))((1/2)+(3/4)+(5/6)) (u/l)=((4×6)/(3×5))+((2×6)/(1×5))+((2×4)/(1×3)) (l/u)=(((1×3×5)/(2×4×6))/((1/2)+(3/4)+(5/6)))=((1×3×5)/(4×6+3×2×6+5×2×4)) ∴ (u/l)+(l/u)=((4×6)/(3×5))+((2×6)/(1×5))+((2×4)/(1×3))+((1×3×5)/(2^2 ×(2×5+3×3+1×6)))
$${a}=\underset{{n}=\mathrm{1}} {\overset{\mathrm{1008}} {\sum}}\frac{\mathrm{2}{n}−\mathrm{1}}{\mathrm{2}{n}},\:{b}=\underset{{n}=\mathrm{1}} {\overset{\mathrm{1008}} {\prod}}\frac{\left(\mathrm{2}{n}−\mathrm{1}\right)}{\left(\mathrm{2}{n}\right)} \\ $$$$\frac{{a}}{{b}}=\frac{\underset{{n}=\mathrm{1}} {\overset{\mathrm{1008}} {\prod}}\left(\mathrm{2}{n}\right)}{\underset{{n}=\mathrm{1}} {\overset{\mathrm{1008}} {\prod}}\left(\mathrm{2}{n}−\mathrm{1}\right)}\underset{{n}=\mathrm{1}} {\overset{\mathrm{1008}} {\sum}}\frac{\mathrm{2}{n}−\mathrm{1}}{\mathrm{2}{n}} \\ $$$$−−−−−−−−−−−−−−−−−−−−− \\ $$$${u}=\frac{\mathrm{1}}{\mathrm{2}}+\frac{\mathrm{3}}{\mathrm{4}}+\frac{\mathrm{5}}{\mathrm{6}} \\ $$$${l}=\frac{\mathrm{1}}{\mathrm{2}}×\frac{\mathrm{3}}{\mathrm{4}}×\frac{\mathrm{5}}{\mathrm{6}} \\ $$$$\therefore\:\frac{{u}}{{l}}=\frac{\mathrm{2}×\mathrm{4}×\mathrm{6}}{\mathrm{1}×\mathrm{3}×\mathrm{5}}\left(\frac{\mathrm{1}}{\mathrm{2}}+\frac{\mathrm{3}}{\mathrm{4}}+\frac{\mathrm{5}}{\mathrm{6}}\right) \\ $$$$\frac{{u}}{{l}}=\frac{\mathrm{4}×\mathrm{6}}{\mathrm{3}×\mathrm{5}}+\frac{\mathrm{2}×\mathrm{6}}{\mathrm{1}×\mathrm{5}}+\frac{\mathrm{2}×\mathrm{4}}{\mathrm{1}×\mathrm{3}} \\ $$$$\frac{{l}}{{u}}=\frac{\frac{\mathrm{1}×\mathrm{3}×\mathrm{5}}{\mathrm{2}×\mathrm{4}×\mathrm{6}}}{\frac{\mathrm{1}}{\mathrm{2}}+\frac{\mathrm{3}}{\mathrm{4}}+\frac{\mathrm{5}}{\mathrm{6}}}=\frac{\mathrm{1}×\mathrm{3}×\mathrm{5}}{\mathrm{4}×\mathrm{6}+\mathrm{3}×\mathrm{2}×\mathrm{6}+\mathrm{5}×\mathrm{2}×\mathrm{4}} \\ $$$$\therefore\:\frac{{u}}{{l}}+\frac{{l}}{{u}}=\frac{\mathrm{4}×\mathrm{6}}{\mathrm{3}×\mathrm{5}}+\frac{\mathrm{2}×\mathrm{6}}{\mathrm{1}×\mathrm{5}}+\frac{\mathrm{2}×\mathrm{4}}{\mathrm{1}×\mathrm{3}}+\frac{\mathrm{1}×\mathrm{3}×\mathrm{5}}{\mathrm{2}^{\mathrm{2}} ×\left(\mathrm{2}×\mathrm{5}+\mathrm{3}×\mathrm{3}+\mathrm{1}×\mathrm{6}\right)} \\ $$$$ \\ $$
Commented by Yozzii last updated on 22/Jun/16
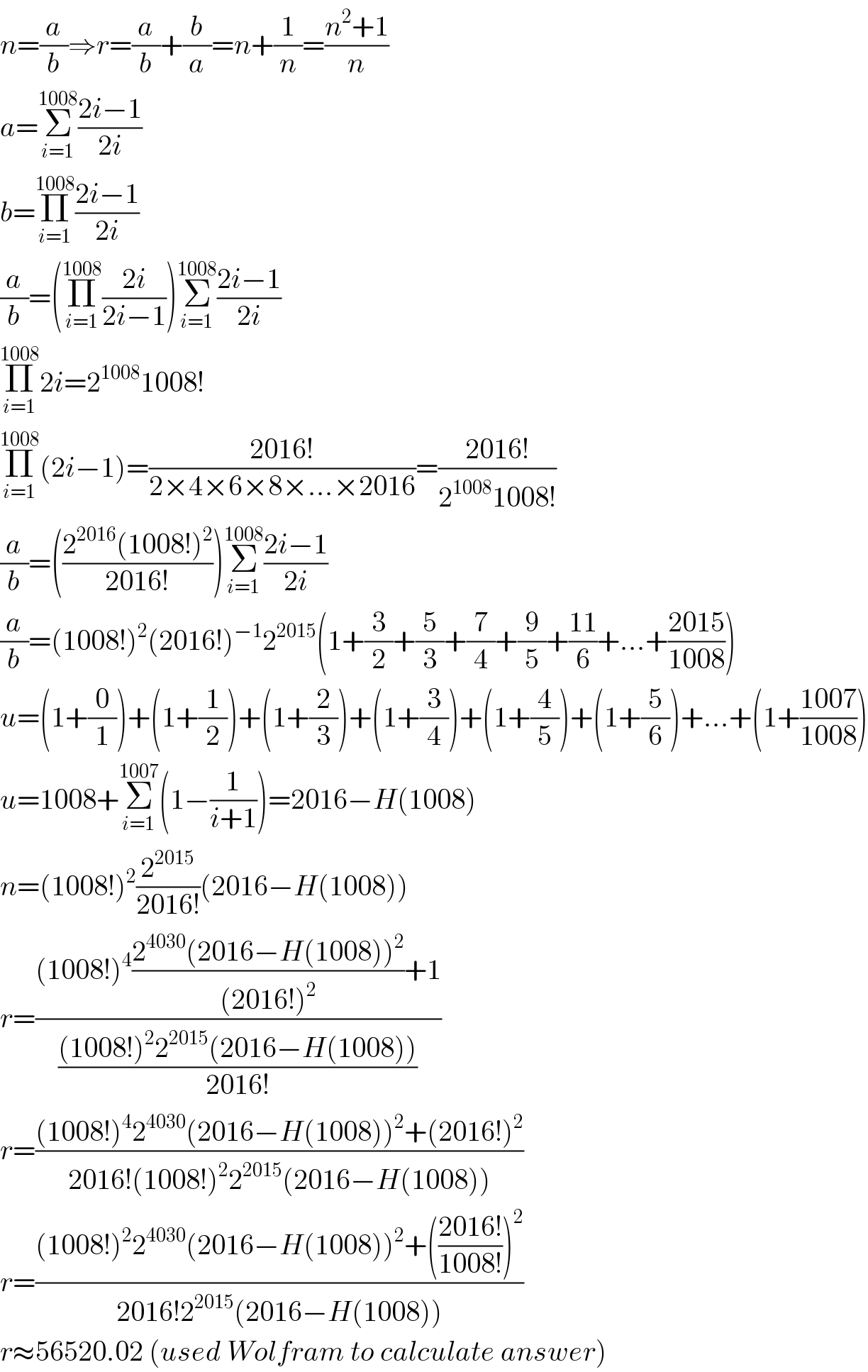
n=(a/b)⇒r=(a/b)+(b/a)=n+(1/n)=((n^2 +1)/n) a=Σ_(i=1) ^(1008) ((2i−1)/(2i)) b=Π_(i=1) ^(1008) ((2i−1)/(2i)) (a/b)=(Π_(i=1) ^(1008) ((2i)/(2i−1)))Σ_(i=1) ^(1008) ((2i−1)/(2i)) Π_(i=1) ^(1008) 2i=2^(1008) 1008! Π_(i=1) ^(1008) (2i−1)=((2016!)/(2×4×6×8×...×2016))=((2016!)/(2^(1008) 1008!)) (a/b)=(((2^(2016) (1008!)^2 )/(2016!)))Σ_(i=1) ^(1008) ((2i−1)/(2i)) (a/b)=(1008!)^2 (2016!)^(−1) 2^(2015) (1+(3/2)+(5/3)+(7/4)+(9/5)+((11)/6)+...+((2015)/(1008))) u=(1+(0/1))+(1+(1/2))+(1+(2/3))+(1+(3/4))+(1+(4/5))+(1+(5/6))+...+(1+((1007)/(1008))) u=1008+Σ_(i=1) ^(1007) (1−(1/(i+1)))=2016−H(1008) n=(1008!)^2 (2^(2015) /(2016!))(2016−H(1008)) r=(((1008!)^4 ((2^(4030) (2016−H(1008))^2 )/((2016!)^2 ))+1)/(((1008!)^2 2^(2015) (2016−H(1008)))/(2016!))) r=(((1008!)^4 2^(4030) (2016−H(1008))^2 +(2016!)^2 )/(2016!(1008!)^2 2^(2015) (2016−H(1008)))) r=(((1008!)^2 2^(4030) (2016−H(1008))^2 +(((2016!)/(1008!)))^2 )/(2016!2^(2015) (2016−H(1008)))) r≈56520.02 (used Wolfram to calculate answer)
$${n}=\frac{{a}}{{b}}\Rightarrow{r}=\frac{{a}}{{b}}+\frac{{b}}{{a}}={n}+\frac{\mathrm{1}}{{n}}=\frac{{n}^{\mathrm{2}} +\mathrm{1}}{{n}} \\ $$$${a}=\underset{{i}=\mathrm{1}} {\overset{\mathrm{1008}} {\sum}}\frac{\mathrm{2}{i}−\mathrm{1}}{\mathrm{2}{i}} \\ $$$${b}=\underset{{i}=\mathrm{1}} {\overset{\mathrm{1008}} {\prod}}\frac{\mathrm{2}{i}−\mathrm{1}}{\mathrm{2}{i}} \\ $$$$\frac{{a}}{{b}}=\left(\underset{{i}=\mathrm{1}} {\overset{\mathrm{1008}} {\prod}}\frac{\mathrm{2}{i}}{\mathrm{2}{i}−\mathrm{1}}\right)\underset{{i}=\mathrm{1}} {\overset{\mathrm{1008}} {\sum}}\frac{\mathrm{2}{i}−\mathrm{1}}{\mathrm{2}{i}} \\ $$$$\underset{{i}=\mathrm{1}} {\overset{\mathrm{1008}} {\prod}}\mathrm{2}{i}=\mathrm{2}^{\mathrm{1008}} \mathrm{1008}! \\ $$$$\underset{{i}=\mathrm{1}} {\overset{\mathrm{1008}} {\prod}}\left(\mathrm{2}{i}−\mathrm{1}\right)=\frac{\mathrm{2016}!}{\mathrm{2}×\mathrm{4}×\mathrm{6}×\mathrm{8}×…×\mathrm{2016}}=\frac{\mathrm{2016}!}{\mathrm{2}^{\mathrm{1008}} \mathrm{1008}!} \\ $$$$\frac{{a}}{{b}}=\left(\frac{\mathrm{2}^{\mathrm{2016}} \left(\mathrm{1008}!\right)^{\mathrm{2}} }{\mathrm{2016}!}\right)\underset{{i}=\mathrm{1}} {\overset{\mathrm{1008}} {\sum}}\frac{\mathrm{2}{i}−\mathrm{1}}{\mathrm{2}{i}} \\ $$$$\frac{{a}}{{b}}=\left(\mathrm{1008}!\right)^{\mathrm{2}} \left(\mathrm{2016}!\right)^{−\mathrm{1}} \mathrm{2}^{\mathrm{2015}} \left(\mathrm{1}+\frac{\mathrm{3}}{\mathrm{2}}+\frac{\mathrm{5}}{\mathrm{3}}+\frac{\mathrm{7}}{\mathrm{4}}+\frac{\mathrm{9}}{\mathrm{5}}+\frac{\mathrm{11}}{\mathrm{6}}+…+\frac{\mathrm{2015}}{\mathrm{1008}}\right) \\ $$$${u}=\left(\mathrm{1}+\frac{\mathrm{0}}{\mathrm{1}}\right)+\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2}}\right)+\left(\mathrm{1}+\frac{\mathrm{2}}{\mathrm{3}}\right)+\left(\mathrm{1}+\frac{\mathrm{3}}{\mathrm{4}}\right)+\left(\mathrm{1}+\frac{\mathrm{4}}{\mathrm{5}}\right)+\left(\mathrm{1}+\frac{\mathrm{5}}{\mathrm{6}}\right)+…+\left(\mathrm{1}+\frac{\mathrm{1007}}{\mathrm{1008}}\right) \\ $$$${u}=\mathrm{1008}+\underset{{i}=\mathrm{1}} {\overset{\mathrm{1007}} {\sum}}\left(\mathrm{1}−\frac{\mathrm{1}}{{i}+\mathrm{1}}\right)=\mathrm{2016}−{H}\left(\mathrm{1008}\right) \\ $$$${n}=\left(\mathrm{1008}!\right)^{\mathrm{2}} \frac{\mathrm{2}^{\mathrm{2015}} }{\mathrm{2016}!}\left(\mathrm{2016}−{H}\left(\mathrm{1008}\right)\right) \\ $$$${r}=\frac{\left(\mathrm{1008}!\right)^{\mathrm{4}} \frac{\mathrm{2}^{\mathrm{4030}} \left(\mathrm{2016}−{H}\left(\mathrm{1008}\right)\right)^{\mathrm{2}} }{\left(\mathrm{2016}!\right)^{\mathrm{2}} }+\mathrm{1}}{\frac{\left(\mathrm{1008}!\right)^{\mathrm{2}} \mathrm{2}^{\mathrm{2015}} \left(\mathrm{2016}−{H}\left(\mathrm{1008}\right)\right)}{\mathrm{2016}!}} \\ $$$${r}=\frac{\left(\mathrm{1008}!\right)^{\mathrm{4}} \mathrm{2}^{\mathrm{4030}} \left(\mathrm{2016}−{H}\left(\mathrm{1008}\right)\right)^{\mathrm{2}} +\left(\mathrm{2016}!\right)^{\mathrm{2}} }{\mathrm{2016}!\left(\mathrm{1008}!\right)^{\mathrm{2}} \mathrm{2}^{\mathrm{2015}} \left(\mathrm{2016}−{H}\left(\mathrm{1008}\right)\right)} \\ $$$${r}=\frac{\left(\mathrm{1008}!\right)^{\mathrm{2}} \mathrm{2}^{\mathrm{4030}} \left(\mathrm{2016}−{H}\left(\mathrm{1008}\right)\right)^{\mathrm{2}} +\left(\frac{\mathrm{2016}!}{\mathrm{1008}!}\right)^{\mathrm{2}} }{\mathrm{2016}!\mathrm{2}^{\mathrm{2015}} \left(\mathrm{2016}−{H}\left(\mathrm{1008}\right)\right)} \\ $$$${r}\approx\mathrm{56520}.\mathrm{02}\:\left({used}\:{Wolfram}\:{to}\:{calculate}\:{answer}\right) \\ $$
Commented by FilupSmith last updated on 22/Jun/16
nice work guys!
$$\mathrm{nice}\:\mathrm{work}\:\mathrm{guys}! \\ $$
Commented by sanusihammed last updated on 22/Jun/16
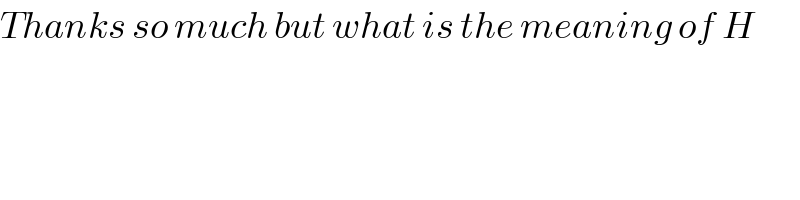
Thanks so much but what is the meaning of H
$${Thanks}\:{so}\:{much}\:{but}\:{what}\:{is}\:{the}\:{meaning}\:{of}\:{H} \\ $$
Commented by Yozzii last updated on 22/Jun/16
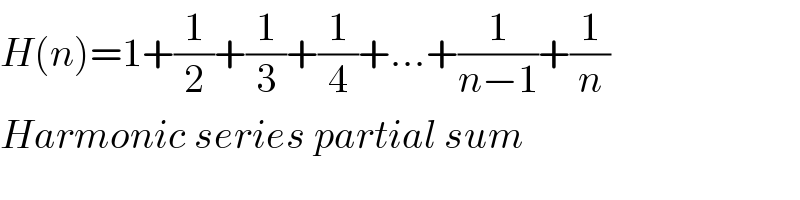
H(n)=1+(1/2)+(1/3)+(1/4)+...+(1/(n−1))+(1/n) Harmonic series partial sum
$${H}\left({n}\right)=\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{3}}+\frac{\mathrm{1}}{\mathrm{4}}+…+\frac{\mathrm{1}}{{n}−\mathrm{1}}+\frac{\mathrm{1}}{{n}} \\ $$$${Harmonic}\:{series}\:{partial}\:{sum} \\ $$
Commented by FilupSmith last updated on 23/Jun/16
Yozzie uses H(n) notation whereas I use H_n notation. Both represent the same thing.
$$\mathrm{Yozzie}\:\mathrm{uses}\:{H}\left({n}\right)\:\mathrm{notation}\:\mathrm{whereas} \\ $$$$\mathrm{I}\:\mathrm{use}\:{H}_{{n}} \:\mathrm{notation}.\:\mathrm{Both}\:\mathrm{represent}\:\mathrm{the} \\ $$$$\mathrm{same}\:\mathrm{thing}. \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *