Question-6432

Question Number 6432 by Rasheed Soomro last updated on 27/Jun/16

Commented by Rasheed Soomro last updated on 27/Jun/16

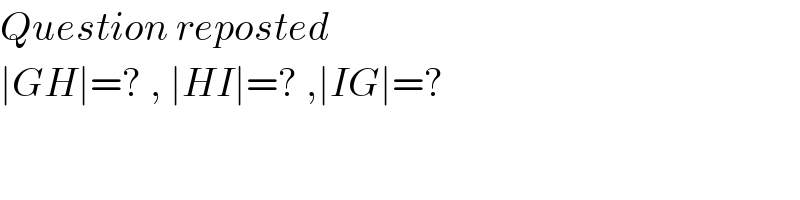
Question reposted ∣GH∣=? , ∣HI∣=? ,∣IG∣=?

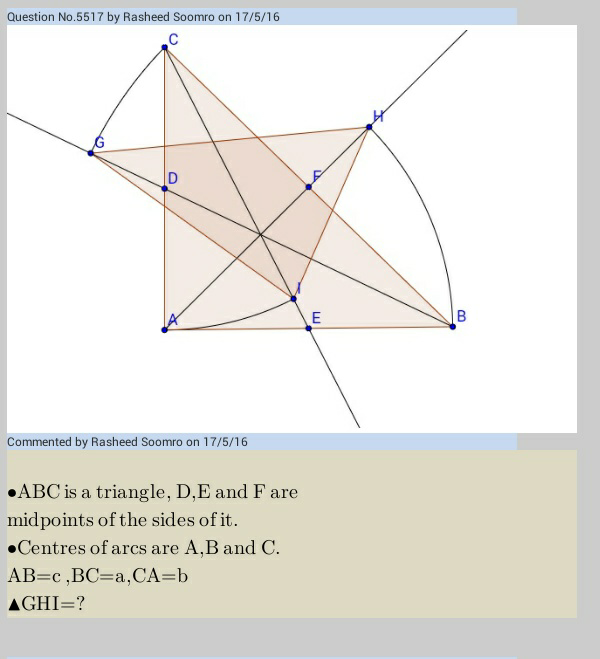
$${Question}\:{reposted} \\ $$$$\mid{GH}\mid=?\:,\:\mid{HI}\mid=?\:,\mid{IG}\mid=? \\ $$

Commented by Yozzii last updated on 01/Jul/16

Vector Analysis Method −−−−−−−−−−−−−−−−−−−−−−−− Let ⟨AB⟩=a and ⟨AC⟩=b. (a≠−b) ⟨AF⟩=a+0.5(b−a)=0.5(a+b). Let ⟨AH⟩=μ⟨AF⟩, μ>0. ∣AH∣=∣AB∣=∣a∣. ∣AH∣=μ∣AF∣⇒μ=((∣AH∣)/(∣AF∣))=((2∣a∣)/(∣a+b∣)). ∴ ⟨AH⟩=((2∣a∣)/(∣a+b∣))0.5(a+b) ⟨AH⟩=((∣a∣)/(∣a+b∣))(a+b). ⟨BD⟩=−a+0.5b. Let ⟨BG⟩=λ⟨BD⟩, λ>0. ⇒λ=((∣BG∣)/(∣BD∣))=((∣CB∣)/(0.5∣b−2a∣))=2((∣a−b∣)/(∣b−2a∣)). ∴⟨BG⟩=((∣a−b∣)/(∣b−2a∣))(b−2a). ⟨AG⟩=⟨AB⟩+⟨BG⟩ ⟨AG⟩=a+((∣a−b∣)/(∣b−2a∣))(b−2a) ⟨AG⟩=(1−((2∣a−b∣)/(∣b−2a∣)))a+((∣a−b∣)/(∣b−2a∣))b. ⟨AH⟩=((∣a∣)/(∣a+b∣))a+((∣a∣)/(∣a+b∣))b ⟨GH⟩=⟨AH⟩−⟨AG⟩ ⟨GH⟩=(−1+((2∣a−b∣)/(∣b−2a∣))+((∣a∣)/(∣a+b∣)))a+(((∣a∣)/(∣a+b∣))−((∣a−b∣)/(∣b−2a∣)))b Let n=−1+((2∣a−b∣)/(∣b−2a∣))+((∣a∣)/(∣a+b∣)) and m=((∣a∣)/(∣a+b∣))−((∣a−b∣)/(∣b−2a∣)). ∴ ⟨GH⟩=na+mb ⇒∣GH∣^2 =⟨GH⟩.⟨GH⟩ ∣GH∣^2 =n^2 a.a+2nma.b+m^2 b.b ∣GH∣=(√(n^2 ∣a∣^2 +m^2 ∣b∣^2 +2mna.b)) Let θ=∠CAB. ∴ a.b=∣a∣∣b∣cosθ ∴∣GH∣=(√(n^2 ∣a∣^2 +m^2 ∣b∣^2 +mn(2∣a∣∣b∣cosθ))) By law of cosines, 2∣a∣∣b∣cosθ=−∣a−b∣^2 +∣a∣^2 +∣b∣^2 ∴∣GH∣=(√(n(n+m)∣a∣^2 +m(m+n)∣b∣^2 −mn∣a−b∣^2 )) ∣GH∣=(√((n+m)(n∣a∣^2 +m∣b∣^2 )−mn∣a−b∣^2 )) It can be shown that ∣a+b∣^2 =2(∣a∣^2 +∣b∣^2 )−∣a−b∣^2 ⇒∣a+b∣=(√(2(∣a∣^2 +∣b∣^2 )−∣a−b∣^2 ))>0 ∣b−2a∣^2 =∣b∣^2 +4∣a∣^2 −2×2∣b∣∣a∣cosθ ∣b−2a∣^2 =−∣b∣^2 +2∣a∣^2 +2∣a−b∣^2 ∣b−2a∣=(√(2(∣a∣^2 +∣a−b∣^2 )−∣b∣^2 )) Let ∣a∣=c>0, ∣b∣=b>0 and ∣a−b∣=a>0. −−−−−−−−−−−−−−−−−−−−−−−−−−− For △GHI constructed from △ABC, in such a way as above, ∴∣GH∣=(√((n+m)(nc^2 +mb^2 )−mna^2 )) where n=−1+((2a)/( (√(2(c^2 +a^2 )−b^2 ))))+(c/( (√(2(c^2 +b^2 )−a^2 )))) m=(c/( (√(2(c^2 +b^2 )−a^2 ))))−(a/( (√(2(c^2 +a^2 )−b^2 )))) −−−−−−−−−−−−−−−−−−−−−−−−− A similar analysis can be used to find the remaining lengths. Try it! (Cyclic permutation of abc I guess is possible.)

$${Vector}\:{Analysis}\:{Method} \\ $$$$−−−−−−−−−−−−−−−−−−−−−−−− \\ $$$${Let}\:\langle{AB}\rangle=\boldsymbol{{a}}\:{and}\:\langle{AC}\rangle=\boldsymbol{{b}}.\:\left(\boldsymbol{{a}}\neq−\boldsymbol{{b}}\right) \\ $$$$\langle{AF}\rangle=\boldsymbol{{a}}+\mathrm{0}.\mathrm{5}\left(\boldsymbol{{b}}−\boldsymbol{{a}}\right)=\mathrm{0}.\mathrm{5}\left(\boldsymbol{{a}}+\boldsymbol{{b}}\right). \\ $$$${Let}\:\langle{AH}\rangle=\mu\langle{AF}\rangle,\:\mu>\mathrm{0}.\:\mid{AH}\mid=\mid{AB}\mid=\mid\boldsymbol{{a}}\mid. \\ $$$$\mid{AH}\mid=\mu\mid{AF}\mid\Rightarrow\mu=\frac{\mid{AH}\mid}{\mid{AF}\mid}=\frac{\mathrm{2}\mid\boldsymbol{{a}}\mid}{\mid\boldsymbol{{a}}+\boldsymbol{{b}}\mid}. \\ $$$$\therefore\:\langle{AH}\rangle=\frac{\mathrm{2}\mid\boldsymbol{{a}}\mid}{\mid\boldsymbol{{a}}+\boldsymbol{{b}}\mid}\mathrm{0}.\mathrm{5}\left(\boldsymbol{{a}}+\boldsymbol{{b}}\right) \\ $$$$\langle{AH}\rangle=\frac{\mid\boldsymbol{{a}}\mid}{\mid\boldsymbol{{a}}+\boldsymbol{{b}}\mid}\left(\boldsymbol{{a}}+\boldsymbol{{b}}\right). \\ $$$$\langle{BD}\rangle=−\boldsymbol{{a}}+\mathrm{0}.\mathrm{5}\boldsymbol{{b}}. \\ $$$${Let}\:\langle{BG}\rangle=\lambda\langle{BD}\rangle,\:\lambda>\mathrm{0}. \\ $$$$\Rightarrow\lambda=\frac{\mid{BG}\mid}{\mid{BD}\mid}=\frac{\mid{CB}\mid}{\mathrm{0}.\mathrm{5}\mid\boldsymbol{{b}}−\mathrm{2}\boldsymbol{{a}}\mid}=\mathrm{2}\frac{\mid\boldsymbol{{a}}−\boldsymbol{{b}}\mid}{\mid\boldsymbol{{b}}−\mathrm{2}\boldsymbol{{a}}\mid}. \\ $$$$\therefore\langle{BG}\rangle=\frac{\mid\boldsymbol{{a}}−\boldsymbol{{b}}\mid}{\mid\boldsymbol{{b}}−\mathrm{2}\boldsymbol{{a}}\mid}\left(\boldsymbol{{b}}−\mathrm{2}\boldsymbol{{a}}\right). \\ $$$$\langle{AG}\rangle=\langle{AB}\rangle+\langle{BG}\rangle \\ $$$$\langle{AG}\rangle=\boldsymbol{{a}}+\frac{\mid\boldsymbol{{a}}−\boldsymbol{{b}}\mid}{\mid\boldsymbol{{b}}−\mathrm{2}\boldsymbol{{a}}\mid}\left(\boldsymbol{{b}}−\mathrm{2}\boldsymbol{{a}}\right) \\ $$$$\langle{AG}\rangle=\left(\mathrm{1}−\frac{\mathrm{2}\mid\boldsymbol{{a}}−\boldsymbol{{b}}\mid}{\mid\boldsymbol{{b}}−\mathrm{2}\boldsymbol{{a}}\mid}\right)\boldsymbol{{a}}+\frac{\mid\boldsymbol{{a}}−\boldsymbol{{b}}\mid}{\mid\boldsymbol{{b}}−\mathrm{2}\boldsymbol{{a}}\mid}\boldsymbol{{b}}. \\ $$$$\langle{AH}\rangle=\frac{\mid\boldsymbol{{a}}\mid}{\mid\boldsymbol{{a}}+\boldsymbol{{b}}\mid}\boldsymbol{{a}}+\frac{\mid\boldsymbol{{a}}\mid}{\mid\boldsymbol{{a}}+\boldsymbol{{b}}\mid}\boldsymbol{{b}} \\ $$$$\langle{GH}\rangle=\langle{AH}\rangle−\langle{AG}\rangle \\ $$$$\langle{GH}\rangle=\left(−\mathrm{1}+\frac{\mathrm{2}\mid\boldsymbol{{a}}−\boldsymbol{{b}}\mid}{\mid\boldsymbol{{b}}−\mathrm{2}\boldsymbol{{a}}\mid}+\frac{\mid\boldsymbol{{a}}\mid}{\mid\boldsymbol{{a}}+\boldsymbol{{b}}\mid}\right)\boldsymbol{{a}}+\left(\frac{\mid\boldsymbol{{a}}\mid}{\mid\boldsymbol{{a}}+\boldsymbol{{b}}\mid}−\frac{\mid\boldsymbol{{a}}−\boldsymbol{{b}}\mid}{\mid\boldsymbol{{b}}−\mathrm{2}\boldsymbol{{a}}\mid}\right)\boldsymbol{{b}} \\ $$$${Let}\:{n}=−\mathrm{1}+\frac{\mathrm{2}\mid\boldsymbol{{a}}−\boldsymbol{{b}}\mid}{\mid\boldsymbol{{b}}−\mathrm{2}\boldsymbol{{a}}\mid}+\frac{\mid\boldsymbol{{a}}\mid}{\mid\boldsymbol{{a}}+\boldsymbol{{b}}\mid}\:{and}\:{m}=\frac{\mid\boldsymbol{{a}}\mid}{\mid\boldsymbol{{a}}+\boldsymbol{{b}}\mid}−\frac{\mid\boldsymbol{{a}}−\boldsymbol{{b}}\mid}{\mid\boldsymbol{{b}}−\mathrm{2}\boldsymbol{{a}}\mid}. \\ $$$$\therefore\:\langle{GH}\rangle={n}\boldsymbol{{a}}+{m}\boldsymbol{{b}} \\ $$$$\Rightarrow\mid{GH}\mid^{\mathrm{2}} =\langle{GH}\rangle.\langle{GH}\rangle \\ $$$$\mid{GH}\mid^{\mathrm{2}} ={n}^{\mathrm{2}} \boldsymbol{{a}}.\boldsymbol{{a}}+\mathrm{2}{nm}\boldsymbol{{a}}.\boldsymbol{{b}}+{m}^{\mathrm{2}} \boldsymbol{{b}}.\boldsymbol{{b}} \\ $$$$\mid{GH}\mid=\sqrt{{n}^{\mathrm{2}} \mid\boldsymbol{{a}}\mid^{\mathrm{2}} +{m}^{\mathrm{2}} \mid\boldsymbol{{b}}\mid^{\mathrm{2}} +\mathrm{2}{mn}\boldsymbol{{a}}.\boldsymbol{{b}}} \\ $$$${Let}\:\theta=\angle{CAB}. \\ $$$$\therefore\:\boldsymbol{{a}}.\boldsymbol{{b}}=\mid\boldsymbol{{a}}\mid\mid\boldsymbol{{b}}\mid{cos}\theta\: \\ $$$$\therefore\mid{GH}\mid=\sqrt{{n}^{\mathrm{2}} \mid\boldsymbol{{a}}\mid^{\mathrm{2}} +{m}^{\mathrm{2}} \mid\boldsymbol{{b}}\mid^{\mathrm{2}} +{mn}\left(\mathrm{2}\mid\boldsymbol{{a}}\mid\mid\boldsymbol{{b}}\mid{cos}\theta\right)} \\ $$$${By}\:{law}\:{of}\:{cosines},\: \\ $$$$\mathrm{2}\mid\boldsymbol{{a}}\mid\mid\boldsymbol{{b}}\mid{cos}\theta=−\mid\boldsymbol{{a}}−\boldsymbol{{b}}\mid^{\mathrm{2}} +\mid\boldsymbol{{a}}\mid^{\mathrm{2}} +\mid\boldsymbol{{b}}\mid^{\mathrm{2}} \\ $$$$\therefore\mid{GH}\mid=\sqrt{{n}\left({n}+{m}\right)\mid\boldsymbol{{a}}\mid^{\mathrm{2}} +{m}\left({m}+{n}\right)\mid\boldsymbol{{b}}\mid^{\mathrm{2}} −{mn}\mid\boldsymbol{{a}}−\boldsymbol{{b}}\mid^{\mathrm{2}} } \\ $$$$\mid{GH}\mid=\sqrt{\left({n}+{m}\right)\left({n}\mid\boldsymbol{{a}}\mid^{\mathrm{2}} +{m}\mid\boldsymbol{{b}}\mid^{\mathrm{2}} \right)−{mn}\mid\boldsymbol{{a}}−\boldsymbol{{b}}\mid^{\mathrm{2}} } \\ $$$${It}\:{can}\:{be}\:{shown}\:{that}\: \\ $$$$\mid\boldsymbol{{a}}+\boldsymbol{{b}}\mid^{\mathrm{2}} =\mathrm{2}\left(\mid\boldsymbol{{a}}\mid^{\mathrm{2}} +\mid\boldsymbol{{b}}\mid^{\mathrm{2}} \right)−\mid\boldsymbol{{a}}−\boldsymbol{{b}}\mid^{\mathrm{2}} \\ $$$$\Rightarrow\mid\boldsymbol{{a}}+\boldsymbol{{b}}\mid=\sqrt{\mathrm{2}\left(\mid\boldsymbol{{a}}\mid^{\mathrm{2}} +\mid\boldsymbol{{b}}\mid^{\mathrm{2}} \right)−\mid\boldsymbol{{a}}−\boldsymbol{{b}}\mid^{\mathrm{2}} }>\mathrm{0} \\ $$$$\mid\boldsymbol{{b}}−\mathrm{2}\boldsymbol{{a}}\mid^{\mathrm{2}} =\mid\boldsymbol{{b}}\mid^{\mathrm{2}} +\mathrm{4}\mid\boldsymbol{{a}}\mid^{\mathrm{2}} −\mathrm{2}×\mathrm{2}\mid\boldsymbol{{b}}\mid\mid\boldsymbol{{a}}\mid{cos}\theta \\ $$$$\mid\boldsymbol{{b}}−\mathrm{2}\boldsymbol{{a}}\mid^{\mathrm{2}} =−\mid\boldsymbol{{b}}\mid^{\mathrm{2}} +\mathrm{2}\mid\boldsymbol{{a}}\mid^{\mathrm{2}} +\mathrm{2}\mid\boldsymbol{{a}}−\boldsymbol{{b}}\mid^{\mathrm{2}} \\ $$$$\mid\boldsymbol{{b}}−\mathrm{2}\boldsymbol{{a}}\mid=\sqrt{\mathrm{2}\left(\mid\boldsymbol{{a}}\mid^{\mathrm{2}} +\mid\boldsymbol{{a}}−\boldsymbol{{b}}\mid^{\mathrm{2}} \right)−\mid\boldsymbol{{b}}\mid^{\mathrm{2}} } \\ $$$${Let}\:\mid\boldsymbol{{a}}\mid={c}>\mathrm{0},\:\mid\boldsymbol{{b}}\mid={b}>\mathrm{0}\:{and}\:\mid\boldsymbol{{a}}−\boldsymbol{{b}}\mid={a}>\mathrm{0}. \\ $$$$−−−−−−−−−−−−−−−−−−−−−−−−−−− \\ $$$${For}\:\bigtriangleup{GHI}\:{constructed}\:{from}\:\bigtriangleup{ABC}, \\ $$$${in}\:{such}\:{a}\:{way}\:{as}\:{above}, \\ $$$$\therefore\mid{GH}\mid=\sqrt{\left({n}+{m}\right)\left({nc}^{\mathrm{2}} +{mb}^{\mathrm{2}} \right)−{mna}^{\mathrm{2}} } \\ $$$$\boldsymbol{{where}} \\ $$$${n}=−\mathrm{1}+\frac{\mathrm{2}{a}}{\:\sqrt{\mathrm{2}\left({c}^{\mathrm{2}} +{a}^{\mathrm{2}} \right)−{b}^{\mathrm{2}} }}+\frac{{c}}{\:\sqrt{\mathrm{2}\left({c}^{\mathrm{2}} +{b}^{\mathrm{2}} \right)−{a}^{\mathrm{2}} }} \\ $$$${m}=\frac{{c}}{\:\sqrt{\mathrm{2}\left({c}^{\mathrm{2}} +{b}^{\mathrm{2}} \right)−{a}^{\mathrm{2}} }}−\frac{{a}}{\:\sqrt{\mathrm{2}\left({c}^{\mathrm{2}} +{a}^{\mathrm{2}} \right)−{b}^{\mathrm{2}} }} \\ $$$$−−−−−−−−−−−−−−−−−−−−−−−−− \\ $$$${A}\:{similar}\:{analysis}\:{can}\:{be}\:{used}\:{to} \\ $$$${find}\:{the}\:{remaining}\:{lengths}.\:{Try}\:{it}! \\ $$$$\left({Cyclic}\:{permutation}\:{of}\:{abc}\:{I}\:{guess}\:{is}\:{possible}.\right) \\ $$

Commented by Rasheed Soomro last updated on 01/Jul/16

THankS! Your approach is always reliable but I need to revise my knowledge about vector analysis.

$$\mathcal{TH}{ank}\mathcal{S}! \\ $$$${Your}\:{approach}\:{is}\:{always}\:{reliable} \\ $$$${but}\:{I}\:{need}\:{to}\:{revise}\:{my}\:{knowledge} \\ $$$${about}\:\mathrm{vector}\:\mathrm{analysis}. \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply