Question Number 6488 by Rasheed Soomro last updated on 29/Jun/16

Commented by Rasheed Soomro last updated on 29/Jun/16

$${Centres}\:{of}\:{the}\:{arcs}\:\:{are}\:\mathrm{A},\mathrm{B}\:{and}\:\mathrm{C}. \\ $$$${Also}\:{determine}\:{the}\:{measures}\:{of}\:{the}\:{sides} \\ $$$${of}\:\bigtriangleup\mathrm{DFH}. \\ $$$${May}\:{be}\:{treated}\:{as}\:{separate}\:{question}\left(\:{labled}\right. \\ $$$$\left.{as}\:{Q}#\mathrm{6488}\:{B}\right) \\ $$
Commented by nburiburu last updated on 29/Jun/16

$${there}\:{is}\:{no}\:{area}\:{if}\:{tbey}\:{are}\:{ortogonal}\:{because} \\ $$$${ABC}\:{would}\:{be}\:{in}\:{I}\:{octant}\:{whileDFH} \\ $$$${would}\:{be}\:{in}\:{VIII}\:{octant}. \\ $$
Commented by Rasheed Soomro last updated on 29/Jun/16
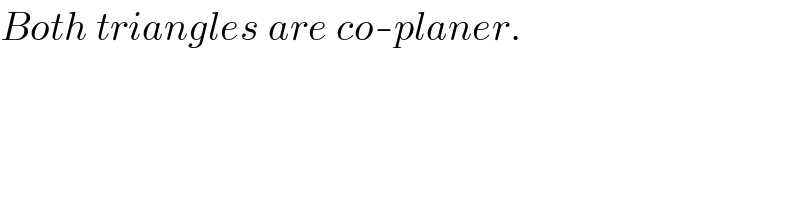
$${Both}\:{triangles}\:{are}\:{co}-{planer}. \\ $$
Commented by nburiburu last updated on 29/Jun/16

$${can}'{t}\:{be}\:{with}\:{the}\:{perpendicularity} \\ $$$${assumed}\:{in}\:{the}\:{hipothesis}.\:{It}\:{says} \\ $$$$“{AD}\:{BF}\:\:{CH}\:{perpendiculars}'' \\ $$
Commented by Rasheed Soomro last updated on 29/Jun/16

$${You}\:{mentioned}\:{in}\:{your}\:{earlier}\:{comment} \\ $$$$“{octants}''.\:{octants}\:{are}\:{build}\:{in}\:{space}\:{when} \\ $$$${xy}-{plane},{yz}-{plane}\:{and}\:{zx}-{plane}\:{cuts}\:{each} \\ $$$${other}\:{orthogonally}\:\left({or}\:{at}\:{any}\:{other}\:{angle}\right). \\ $$$${So}\:{I}\:{thought}\:{that}\:{you}\:{are}\:{seeing}\:{the}\:{two} \\ $$$${triangles}\:{in}\:{a}\:{space}… \\ $$$$ \\ $$
Commented by nburiburu last updated on 30/Jun/16
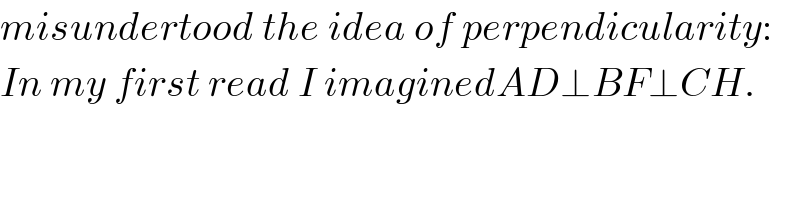
$${misundertood}\:{the}\:{idea}\:{of}\:{perpendicularity}: \\ $$$${In}\:{my}\:{first}\:{read}\:{I}\:{imaginedAD}\bot{BF}\bot{CH}. \\ $$$$ \\ $$
Commented by Rasheed Soomro last updated on 30/Jun/16
![There may be cases even in a plane when the area of the region may be zero or negative[?]. When I was experimenting with the diagram in geogebra(increasing/decreasing sides) the region was disappearing at a time(even the diagram of then was fulfilling the conditions given above).](https://www.tinkutara.com/question/Q6514.png)
$${There}\:{may}\:{be}\:{cases}\:{even}\:{in}\:{a}\:{plane} \\ $$$${when}\:{the}\:{area}\:{of}\:{the}\:{region}\:{may}\:{be} \\ $$$${zero}\:{or}\:{negative}\left[?\right].\:{When}\:{I}\:{was}\: \\ $$$${experimenting}\:{with}\:{the}\:{diagram} \\ $$$${in}\:{geogebra}\left({increasing}/{decreasing}\right. \\ $$$$\left.{sides}\right)\:{the}\:{region}\:{was}\:{disappearing} \\ $$$${at}\:{a}\:{time}\left({even}\:{the}\:{diagram}\:{of}\:{then}\:{was}\right. \\ $$$$\left.{fulfilling}\:{the}\:{conditions}\:{given}\:{above}\right). \\ $$
Answered by nburiburu last updated on 01/Jul/16
![Using vectorial algebra, let say A=(0,0) B=(c,0) C=(x_c ,y_c ) where ∥AC∥= b and ∥BC∥=a so − { ((x_c ^2 +y_c ^2 =b^2 )),(((x_c −c)^2 +y_c ^2 =a^2 )) :} ⇒(x_c −c)^2 −x_c ^2 =a^2 −b^2 −2cx_c +c^2 =a^2 −b^2 ⇒ x_c =((−a^2 +b^2 +c^2 )/(2c)) so y_c =(√(b^2 −x_c ^2 ))=(√((4b^2 c^2 −(−a^2 +b^2 +c^2 )^2 )/(4c^2 ))) y_c =((√([−a^2 +(b+c)^2 ]∙[a^2 −(b−c)^2 ]))/(2c)) Now let find P,Q,R ortogonal proyection of A,B,C respectively. R =(x_c ,0) Q=Proy_(AC^(→) ) ^(→) (AB^(→) )=(((0,c)•(x_c ,y_c ))/(∥x_c ,y_c ∥^2 ))∙(x_c ,y_c ) Q=((c/b^2 )x_c y_c ,(c/b^2 )y_c ^2 ) P =Proy_(BC^(→) ) ^(→) (BA^(→) )+B P=(((0,−c)•(x_c ,y_c −c))/(∥x_c ,y_c −c∥^2 ))∙(x_c ,y_c −c)+(0,c) P=(((c(c−y_c ))/(x_c ^2 +(y_c −c)^2 ))∙x_c ,((−c(y_c −c)^2 )/(x_c ^2 +(y_c −c)^2 ))+c) and now to find D,F,H the idea is to make vectors with AP^(→) ,BQ^(→) ,CR^(→) direction and distance c,a,b respectively D = (c/(∥AP∥))∙AP^(→) F=(a/(∥BQ∥))∙BQ^(→) +B H=(b/(∥CR∥))∙CR^(→) +C and DF, FH, HD can befound. shall continue soon](https://www.tinkutara.com/question/Q6547.png)
$${Using}\:{vectorial}\:{algebra},\:{let}\:{say} \\ $$$${A}=\left(\mathrm{0},\mathrm{0}\right)\: \\ $$$${B}=\left({c},\mathrm{0}\right) \\ $$$${C}=\left({x}_{{c}} ,{y}_{{c}} \right)\:{where}\:\parallel{AC}\parallel=\:{b}\:{and}\:\parallel{BC}\parallel={a} \\ $$$${so} \\ $$$$−\begin{cases}{{x}_{{c}} ^{\mathrm{2}} +{y}_{{c}} ^{\mathrm{2}} ={b}^{\mathrm{2}} }\\{\left({x}_{{c}} −{c}\right)^{\mathrm{2}} +{y}_{{c}} ^{\mathrm{2}} ={a}^{\mathrm{2}} }\end{cases} \\ $$$$\Rightarrow\left({x}_{{c}} −{c}\right)^{\mathrm{2}} −{x}_{{c}} ^{\mathrm{2}} ={a}^{\mathrm{2}} −{b}^{\mathrm{2}} \\ $$$$−\mathrm{2}{cx}_{{c}} +{c}^{\mathrm{2}} ={a}^{\mathrm{2}} −{b}^{\mathrm{2}} \Rightarrow\:{x}_{{c}} =\frac{−{a}^{\mathrm{2}} +{b}^{\mathrm{2}} +{c}^{\mathrm{2}} }{\mathrm{2}{c}}\: \\ $$$${so}\:{y}_{{c}} =\sqrt{{b}^{\mathrm{2}} −{x}_{{c}} ^{\mathrm{2}} }=\sqrt{\frac{\mathrm{4}{b}^{\mathrm{2}} {c}^{\mathrm{2}} −\left(−{a}^{\mathrm{2}} +{b}^{\mathrm{2}} +{c}^{\mathrm{2}} \right)^{\mathrm{2}} }{\mathrm{4}{c}^{\mathrm{2}} }} \\ $$$${y}_{{c}} =\frac{\sqrt{\left[−{a}^{\mathrm{2}} +\left({b}+{c}\right)^{\mathrm{2}} \right]\centerdot\left[{a}^{\mathrm{2}} −\left({b}−{c}\right)^{\mathrm{2}} \right]}}{\mathrm{2}{c}} \\ $$$${Now}\:{let}\:{find}\:{P},{Q},{R}\:{ortogonal}\:{proyection} \\ $$$${of}\:{A},{B},{C}\:{respectively}. \\ $$$${R}\:=\left({x}_{{c}} ,\mathrm{0}\right) \\ $$$${Q}=\overset{\rightarrow} {{Proy}_{\overset{\rightarrow} {{AC}}} }\left(\overset{\rightarrow} {{AB}}\right)=\frac{\left(\mathrm{0},{c}\right)\bullet\left({x}_{{c}} ,{y}_{{c}} \right)}{\parallel{x}_{{c}} ,{y}_{{c}} \parallel^{\mathrm{2}} }\centerdot\left({x}_{{c}} ,{y}_{{c}} \right) \\ $$$${Q}=\left(\frac{{c}}{{b}^{\mathrm{2}} }{x}_{{c}} {y}_{{c}} ,\frac{{c}}{{b}^{\mathrm{2}} }{y}_{{c}} ^{\mathrm{2}} \right) \\ $$$${P}\:=\overset{\rightarrow} {{Proy}_{\overset{\rightarrow} {{BC}}} }\left(\overset{\rightarrow} {{BA}}\right)+{B} \\ $$$${P}=\frac{\left(\mathrm{0},−{c}\right)\bullet\left({x}_{{c}} ,{y}_{{c}} −{c}\right)}{\parallel{x}_{{c}} ,{y}_{{c}} −{c}\parallel^{\mathrm{2}} }\centerdot\left({x}_{{c}} ,{y}_{{c}} −{c}\right)+\left(\mathrm{0},{c}\right) \\ $$$${P}=\left(\frac{{c}\left({c}−{y}_{{c}} \right)}{{x}_{{c}} ^{\mathrm{2}} +\left({y}_{{c}} −{c}\right)^{\mathrm{2}} }\centerdot{x}_{{c}} ,\frac{−{c}\left({y}_{{c}} −{c}\right)^{\mathrm{2}} }{{x}_{{c}} ^{\mathrm{2}} +\left({y}_{{c}} −{c}\right)^{\mathrm{2}} }+{c}\right) \\ $$$${and}\:{now}\:{to}\:{find}\:{D},{F},{H}\:{the}\:{idea}\:{is}\:{to} \\ $$$${make}\:{vectors}\:{with}\:\overset{\rightarrow} {{AP}},\overset{\rightarrow} {{BQ}},\overset{\rightarrow} {{CR}}\:{direction} \\ $$$${and}\:{distance}\:{c},{a},{b}\:{respectively} \\ $$$${D}\:=\:\frac{{c}}{\parallel{AP}\parallel}\centerdot\overset{\rightarrow} {{AP}} \\ $$$${F}=\frac{{a}}{\parallel{BQ}\parallel}\centerdot\overset{\rightarrow} {{BQ}}+{B} \\ $$$${H}=\frac{{b}}{\parallel{CR}\parallel}\centerdot\overset{\rightarrow} {{CR}}+{C} \\ $$$${and}\:{DF},\:{FH},\:{HD}\:{can}\:{befound}. \\ $$$${shall}\:{continue}\:{soon} \\ $$
Commented by Rasheed Soomro last updated on 03/Jul/16
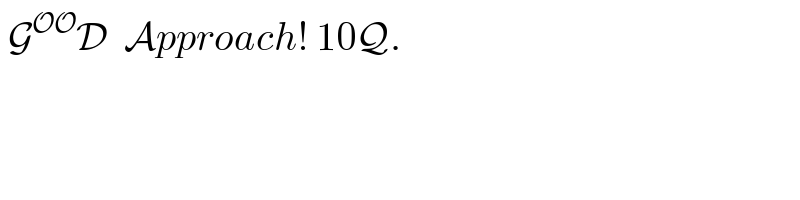
$$\:\mathcal{G}^{\mathcal{OO}} \mathcal{D}\:\:\mathcal{A}{pproach}!\:\mathrm{10}\mathcal{Q}. \\ $$
