Question Number 6553 by Rasheed Soomro last updated on 01/Jul/16

Commented by Rasheed Soomro last updated on 01/Jul/16
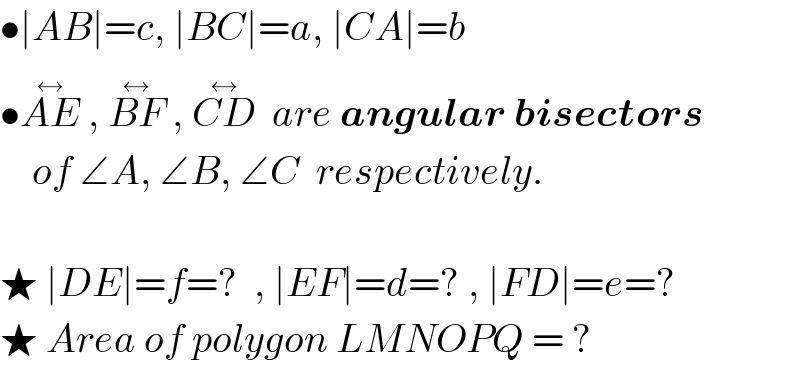
$$\bullet\mid{AB}\mid={c},\:\mid{BC}\mid={a},\:\mid{CA}\mid={b} \\ $$$$\bullet\overset{\leftrightarrow} {{AE}}\:,\:\overset{\leftrightarrow} {{BF}}\:,\:\overset{\leftrightarrow} {{CD}}\:\:{are}\:\boldsymbol{{angular}}\:\boldsymbol{{bisectors}} \\ $$$$\:\:\:\:{of}\:\angle{A},\:\angle{B},\:\angle{C}\:\:{respectively}. \\ $$$$ \\ $$$$\bigstar\:\mid{DE}\mid={f}=?\:\:,\:\mid{EF}\mid={d}=?\:,\:\mid{FD}\mid={e}=? \\ $$$$\bigstar\:{Area}\:{of}\:{polygon}\:{LMNOPQ}\:=\:? \\ $$
Commented by Rasheed Soomro last updated on 01/Jul/16

$${Series}\:{of}\:{questions}\:{of}\:{general}\:{triangle} \\ $$$$\left({similar}\:{to}\:{above}\right)\:{is}\:{completed}\:{with} \\ $$$${this}\:{last}\:{question}.{The}\:{list}\:{is}\:{given}\:{below}: \\ $$$$\bullet{Triangle}\:{with}\:\boldsymbol{{median}}\:{lines} \\ $$$$\bullet{Triangle}\:{with}\:\boldsymbol{{altitude}}\:\:{lines} \\ $$$$\bullet{Triangle}\:{with}\:\boldsymbol{{angular}}\:\boldsymbol{{bisector}}\:{lines} \\ $$$$ \\ $$$$\boldsymbol{\mathrm{Thanks}}\:\boldsymbol{\mathrm{to}}\:\boldsymbol{\mathrm{forum}}-\boldsymbol{\mathrm{friends}}\:\boldsymbol{\mathrm{for}}\:\boldsymbol{\mathrm{cooperation}}! \\ $$
Commented by Yozzii last updated on 04/Jul/16

$${For}\:{the}\:{part}\:{concerning}\:{the}\:{area}\:{of}\:{the} \\ $$$${polygon},\:{it}\:{can}\:{be}\:{found}\:{by}\:\left(\mathrm{1}\right)\:{finding}\:{the} \\ $$$${total}\:{area}\:{of}\:{the}\:'{generated}'\:{triangle} \\ $$$${that}\:{lies}\:{outside}\:{the}\:{original}\:{triangle} \\ $$$${and}\:{then}\:\left(\mathrm{2}\right)\:{subtract}\:{from}\:{the}\:{area}\:{of} \\ $$$${the}\:{generated}\:{triangle}\:{the}\:{result}\:{of}\:\left(\mathrm{1}\right). \\ $$$${By}\:{the}\:{vector}\:{analysis}\:{I}\:{shared}\:{on}\: \\ $$$${one}\:{of}\:{your}\:{posts},\:{you}'{d}\:{need}\:{to}\:{find} \\ $$$${the}\:{vertices}\:{of}\:{each}\:{of}\:{the}\:{external}\: \\ $$$${triangles},\:{calculate}\:{the}\:{sides}\:{of}\:{each} \\ $$$${triangle}\:{and}\:{apply}\:{Heron}'{s}\:{formula}\:\left({or}\:{use}\right. \\ $$$${any}\:{other}\:{method}\:{for}\:{finding}\:{the}\:{area}\:{of}\:{a}\:{triangle}\: \\ $$$$\left.{given}\:{its}\:{side}\:{lengths}\right) \\ $$$${for}\:{each}\:{to}\:{find}\:{the}\:{total}\:{answer}\:{for} \\ $$$${part}\:\left(\mathrm{1}\right).\:{This}\:{method}\:{I}'{ve}\:{described}\:{works} \\ $$$${but}\:{it}\:{is}\:{rather}\:{long}\:{to}\:{type}\:{here}\:{given}\:{the}\: \\ $$$${multitude}\:{of}\:{assumptions}\:{and}\:{conditions} \\ $$$${that}\:{would}\:{need}\:{to}\:{be}\:{delineated}\:{in}\:{a} \\ $$$${formal}\:{answer}. \\ $$$$ \\ $$
Commented by Yozzii last updated on 04/Jul/16

Commented by Yozzii last updated on 04/Jul/16

$${Here},\:{there}\:{are}\:{two}\:{external}\:{triangles}. \\ $$$${Your}\:{diagram}\:{has}\:{three}\:{external}\:{triangles}. \\ $$$${This}\:{diagram}\:{is}\:{based}\:{on}\:{angle}\:{bisectors}. \\ $$
Commented by Yozzii last updated on 04/Jul/16

Commented by Yozzii last updated on 04/Jul/16
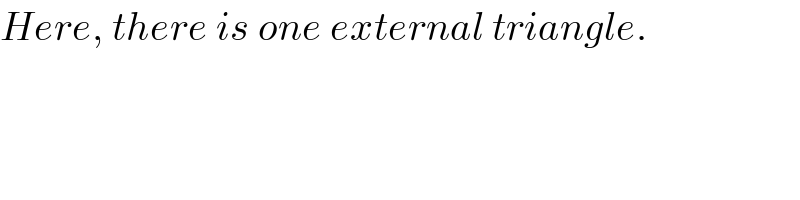
$${Here},\:{there}\:{is}\:{one}\:{external}\:{triangle}. \\ $$
Commented by Rasheed Soomro last updated on 04/Jul/16

$$\mathcal{TH}{ank}\mathcal{S}\:{for}\:\boldsymbol{{good}}\:\boldsymbol{{analysis}}\:\:{of}\:{the}\:{problem} \\ $$$${and}\:{guiding}\:{to}\:{a}\:{way}\:{of}\:{solution}. \\ $$$$ \\ $$
Commented by Rasheed Soomro last updated on 04/Jul/16

$$\bullet{The}\:{problems}\:{can}\:{be}\:{extended}\:{to}\:{any} \\ $$$${n}-{sided}\:{polygon}\:{in}\:{a}\:{variety}\:{of}\:{ways}! \\ $$$$ \\ $$$$\bullet{Also}\:{they}\:{can}\:{be}\:{extended}\:{to}\:{a}\:{general} \\ $$$${polygon}. \\ $$
Commented by Yozzii last updated on 04/Jul/16

$${Yes}\:{yes}. \\ $$
