Menu Close

Question-65680

Tinku Tara
Pin




Question Number 65680 by bshahid010@gmail.com last updated on 01/Aug/19
Answered by mr W last updated on 02/Aug/19
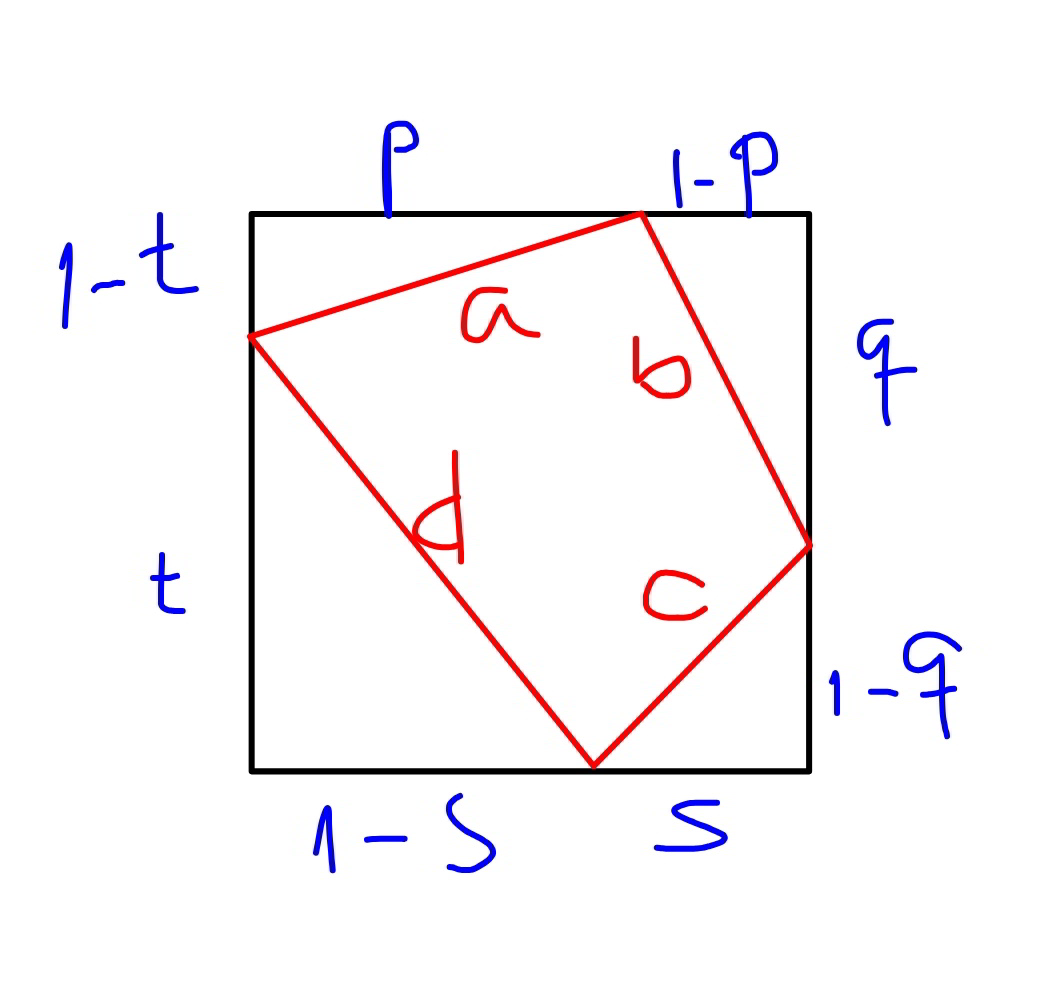
Commented by mr W last updated on 02/Aug/19
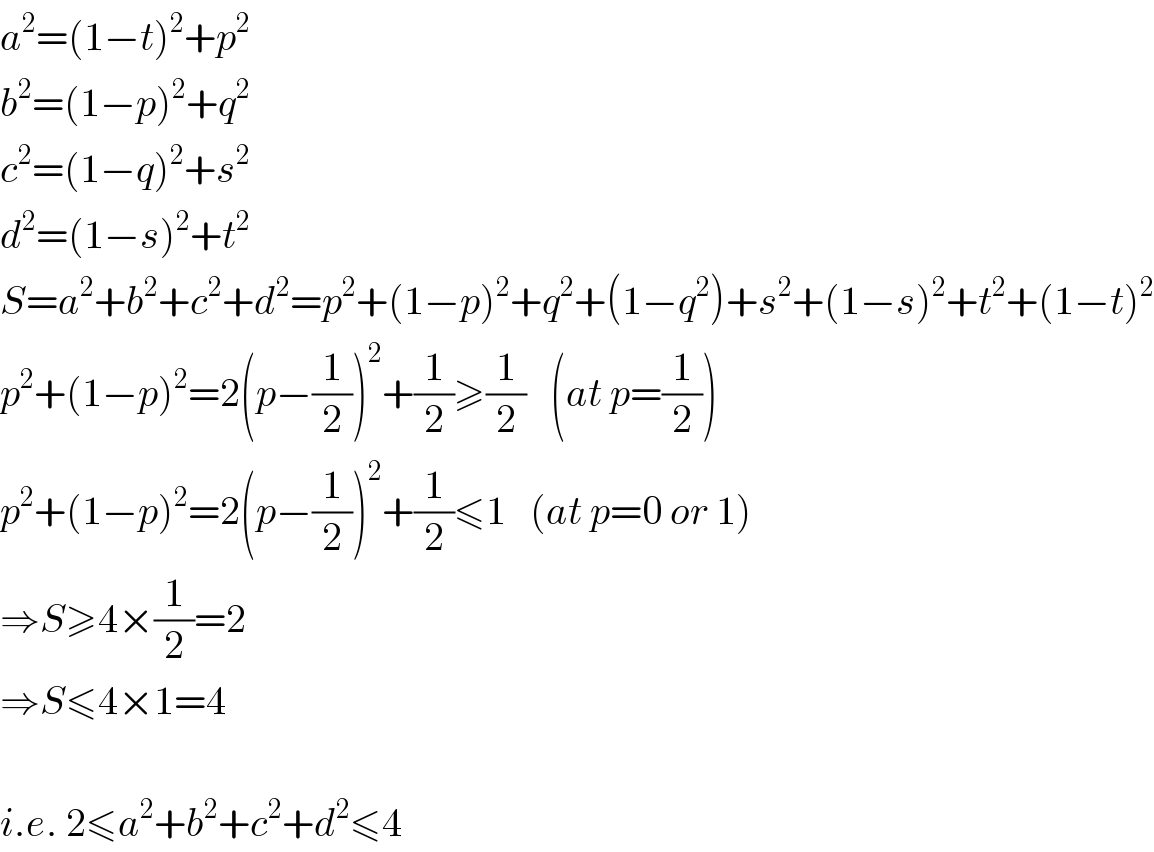
a^2 =(1−t)^2 +p^2 b^2 =(1−p)^2 +q^2 c^2 =(1−q)^2 +s^2 d^2 =(1−s)^2 +t^2 S=a^2 +b^2 +c^2 +d^2 =p^2 +(1−p)^2 +q^2 +(1−q^2 )+s^2 +(1−s)^2 +t^2 +(1−t)^2 p^2 +(1−p)^2 =2(p−(1/2))^2 +(1/2)≥(1/2) (at p=(1/2)) p^2 +(1−p)^2 =2(p−(1/2))^2 +(1/2)≤1 (at p=0 or 1) ⇒S≥4×(1/2)=2 ⇒S≤4×1=4 i.e. 2≤a^2 +b^2 +c^2 +d^2 ≤4
$${a}^{\mathrm{2}} =\left(\mathrm{1}−{t}\right)^{\mathrm{2}} +{p}^{\mathrm{2}} \\ $$$${b}^{\mathrm{2}} =\left(\mathrm{1}−{p}\right)^{\mathrm{2}} +{q}^{\mathrm{2}} \\ $$$${c}^{\mathrm{2}} =\left(\mathrm{1}−{q}\right)^{\mathrm{2}} +{s}^{\mathrm{2}} \\ $$$${d}^{\mathrm{2}} =\left(\mathrm{1}−{s}\right)^{\mathrm{2}} +{t}^{\mathrm{2}} \\ $$$${S}={a}^{\mathrm{2}} +{b}^{\mathrm{2}} +{c}^{\mathrm{2}} +{d}^{\mathrm{2}} ={p}^{\mathrm{2}} +\left(\mathrm{1}−{p}\right)^{\mathrm{2}} +{q}^{\mathrm{2}} +\left(\mathrm{1}−{q}^{\mathrm{2}} \right)+{s}^{\mathrm{2}} +\left(\mathrm{1}−{s}\right)^{\mathrm{2}} +{t}^{\mathrm{2}} +\left(\mathrm{1}−{t}\right)^{\mathrm{2}} \\ $$$${p}^{\mathrm{2}} +\left(\mathrm{1}−{p}\right)^{\mathrm{2}} =\mathrm{2}\left({p}−\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} +\frac{\mathrm{1}}{\mathrm{2}}\geqslant\frac{\mathrm{1}}{\mathrm{2}}\:\:\:\left({at}\:{p}=\frac{\mathrm{1}}{\mathrm{2}}\right) \\ $$$${p}^{\mathrm{2}} +\left(\mathrm{1}−{p}\right)^{\mathrm{2}} =\mathrm{2}\left({p}−\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} +\frac{\mathrm{1}}{\mathrm{2}}\leqslant\mathrm{1}\:\:\:\left({at}\:{p}=\mathrm{0}\:{or}\:\mathrm{1}\right) \\ $$$$\Rightarrow{S}\geqslant\mathrm{4}×\frac{\mathrm{1}}{\mathrm{2}}=\mathrm{2} \\ $$$$\Rightarrow{S}\leqslant\mathrm{4}×\mathrm{1}=\mathrm{4} \\ $$$$ \\ $$$${i}.{e}.\:\mathrm{2}\leqslant{a}^{\mathrm{2}} +{b}^{\mathrm{2}} +{c}^{\mathrm{2}} +{d}^{\mathrm{2}} \leqslant\mathrm{4} \\ $$

Pin