Question Number 65724 by bshahid010@gmail.com last updated on 02/Aug/19
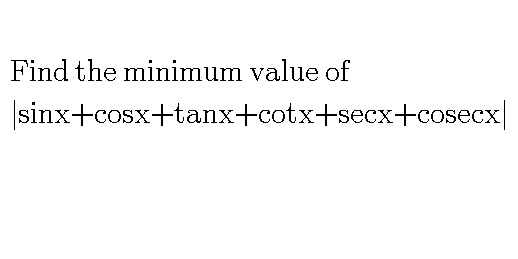
Answered by mr W last updated on 03/Aug/19
![S=sin x+cos x+(1/(sin x))+(1/(cos x))+((sin x)/(cos x))+((cos x)/(sin x)) =sin x+cos x+((sin x+cos x)/(sin x cos x))+(1/(sin x cos x)) =sin x+cos x+((sin x+cos x+1)/(sin x cos x)) let sin x+cos x=t ⇒sin x cos x=((t^2 −1)/2) ⇒S=t+((2(t+1))/(t^2 −1))=t+(2/(t−1))=1+(t−1)+(2/(t−1)) since −(√2)≤t≤(√2) −(√2)−1≤t−1≤(√2)−1 for t−1>0: S=1+(t−1)+(2/(t−1))≥1+2(√2)=S_(min) S_(min) at t=(√2)+1>(√2) ⇒impossible for t−1<0: S=1−[(1−t)+(2/(1−t))]≤1−2(√2)=S_(max) S_(max) at t=1−(√2)>−(√2) ⇒possible ⇒mininmum of ∣S∣ is ∣1−2(√2)∣=2(√2)−1≈1.828 at t=1−(√2) or x=nπ−(−1)^n (sin^(−1) ((2−(√2))/2))−(π/4)](https://www.tinkutara.com/question/Q65738.png)
$${S}=\mathrm{sin}\:{x}+\mathrm{cos}\:{x}+\frac{\mathrm{1}}{\mathrm{sin}\:{x}}+\frac{\mathrm{1}}{\mathrm{cos}\:{x}}+\frac{\mathrm{sin}\:{x}}{\mathrm{cos}\:{x}}+\frac{\mathrm{cos}\:{x}}{\mathrm{sin}\:{x}} \\ $$$$=\mathrm{sin}\:{x}+\mathrm{cos}\:{x}+\frac{\mathrm{sin}\:{x}+\mathrm{cos}\:{x}}{\mathrm{sin}\:{x}\:\mathrm{cos}\:{x}}+\frac{\mathrm{1}}{\mathrm{sin}\:{x}\:\mathrm{cos}\:{x}} \\ $$$$=\mathrm{sin}\:{x}+\mathrm{cos}\:{x}+\frac{\mathrm{sin}\:{x}+\mathrm{cos}\:{x}+\mathrm{1}}{\mathrm{sin}\:{x}\:\mathrm{cos}\:{x}} \\ $$$${let}\:\mathrm{sin}\:{x}+\mathrm{cos}\:{x}={t} \\ $$$$\Rightarrow\mathrm{sin}\:{x}\:\mathrm{cos}\:{x}=\frac{{t}^{\mathrm{2}} −\mathrm{1}}{\mathrm{2}} \\ $$$$\Rightarrow{S}={t}+\frac{\mathrm{2}\left({t}+\mathrm{1}\right)}{{t}^{\mathrm{2}} −\mathrm{1}}={t}+\frac{\mathrm{2}}{{t}−\mathrm{1}}=\mathrm{1}+\left({t}−\mathrm{1}\right)+\frac{\mathrm{2}}{{t}−\mathrm{1}} \\ $$$${since}\:−\sqrt{\mathrm{2}}\leqslant{t}\leqslant\sqrt{\mathrm{2}} \\ $$$$−\sqrt{\mathrm{2}}−\mathrm{1}\leqslant{t}−\mathrm{1}\leqslant\sqrt{\mathrm{2}}−\mathrm{1} \\ $$$$ \\ $$$${for}\:{t}−\mathrm{1}>\mathrm{0}: \\ $$$${S}=\mathrm{1}+\left({t}−\mathrm{1}\right)+\frac{\mathrm{2}}{{t}−\mathrm{1}}\geqslant\mathrm{1}+\mathrm{2}\sqrt{\mathrm{2}}={S}_{{min}} \\ $$$${S}_{{min}} \:{at}\:{t}=\sqrt{\mathrm{2}}+\mathrm{1}>\sqrt{\mathrm{2}}\:\Rightarrow{impossible} \\ $$$$ \\ $$$${for}\:{t}−\mathrm{1}<\mathrm{0}: \\ $$$${S}=\mathrm{1}−\left[\left(\mathrm{1}−{t}\right)+\frac{\mathrm{2}}{\mathrm{1}−{t}}\right]\leqslant\mathrm{1}−\mathrm{2}\sqrt{\mathrm{2}}={S}_{{max}} \\ $$$${S}_{{max}} \:{at}\:{t}=\mathrm{1}−\sqrt{\mathrm{2}}>−\sqrt{\mathrm{2}}\:\Rightarrow{possible} \\ $$$$ \\ $$$$\Rightarrow{mininmum}\:{of}\:\mid{S}\mid\:{is}\:\mid\mathrm{1}−\mathrm{2}\sqrt{\mathrm{2}}\mid=\mathrm{2}\sqrt{\mathrm{2}}−\mathrm{1}\approx\mathrm{1}.\mathrm{828} \\ $$$${at}\:{t}=\mathrm{1}−\sqrt{\mathrm{2}}\:{or}\:{x}={n}\pi−\left(−\mathrm{1}\right)^{{n}} \left(\mathrm{sin}^{−\mathrm{1}} \frac{\mathrm{2}−\sqrt{\mathrm{2}}}{\mathrm{2}}\right)−\frac{\pi}{\mathrm{4}} \\ $$
Answered by Tanmay chaudhury last updated on 03/Aug/19

$${sinx}+{cosx}={a} \\ $$$$\sqrt{\mathrm{2}}\:\left(\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}{sinx}+\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}{cosx}\right)={a} \\ $$$$\sqrt{\mathrm{2}}\:{sin}\left(\frac{\pi}{\mathrm{4}}+{x}\right)={a} \\ $$$$+\mathrm{1}\geqslant{sin}\left(\frac{\pi}{\mathrm{4}}+{x}\right)\geqslant−\mathrm{1} \\ $$$${so}\:\sqrt{\mathrm{2}}\geqslant\:{a}\geqslant−\sqrt{\mathrm{2}}\: \\ $$$${tanx}+{cotx} \\ $$$$\frac{{sin}^{\mathrm{2}} {x}+{cos}^{\mathrm{2}} {x}}{{cosxsinx}} \\ $$$$\frac{\mathrm{2}}{\mathrm{2}{sinxcosx}} \\ $$$$\frac{\mathrm{2}}{{sin}\mathrm{2}{x}} \\ $$$$\frac{\mathrm{2}}{\mathrm{1}+{sin}\mathrm{2}{x}−\mathrm{1}} \\ $$$$\frac{\mathrm{2}}{\left({sinx}+{cosx}\right)^{\mathrm{2}} −\mathrm{1}} \\ $$$$\frac{\mathrm{2}}{{a}^{\mathrm{2}} −\mathrm{1}} \\ $$$${secx}+{cosecx} \\ $$$$=\frac{{sinx}+{cosx}}{{sinxcosx}} \\ $$$$=\left({sinx}+{cosx}\right)×\frac{\mathrm{1}}{{sinxcosx}} \\ $$$$=\left({sinx}+{cosx}\right)×\frac{\mathrm{2}}{\mathrm{2}{sinxcosx}} \\ $$$$={a}×\frac{\mathrm{2}}{{a}^{\mathrm{2}} −\mathrm{1}} \\ $$$$\boldsymbol{{so}}\:\boldsymbol{{sinx}}+\boldsymbol{{cosx}}+\boldsymbol{{tanx}}+\boldsymbol{{cotx}}+\boldsymbol{{secx}}+\boldsymbol{{cosecx}} \\ $$$$=\boldsymbol{{a}}+\frac{\mathrm{2}}{\boldsymbol{{a}}^{\mathrm{2}} −\mathrm{1}}+\frac{\mathrm{2}\boldsymbol{{a}}}{\boldsymbol{{a}}^{\mathrm{2}} −\mathrm{1}} \\ $$$$=\boldsymbol{{a}}+\frac{\mathrm{2}\left(\boldsymbol{{a}}+\mathrm{1}\right)}{\left(\boldsymbol{{a}}+\mathrm{1}\right)\left(\boldsymbol{{a}}−\mathrm{1}\right)} \\ $$$$=\boldsymbol{{a}}+\frac{\mathrm{2}}{\boldsymbol{{a}}−\mathrm{1}} \\ $$$$\boldsymbol{{when}}\:\boldsymbol{{a}}=\sqrt{\mathrm{2}}\: \\ $$$$=\frac{\sqrt{\mathrm{2}}}{\mathrm{1}}+\frac{\mathrm{2}}{\:\sqrt{\mathrm{2}}\:−\mathrm{1}} \\ $$$$=\sqrt{\mathrm{2}}\:+\mathrm{2}\left(\sqrt{\mathrm{2}}\:+\mathrm{1}\right) \\ $$$$=\mathrm{3}\sqrt{\mathrm{2}}\:+\mathrm{2} \\ $$$$=\mathrm{3}×\mathrm{1}.\mathrm{41}+\mathrm{2} \\ $$$$=\mathrm{6}.\mathrm{23} \\ $$$$\boldsymbol{{so}}\:\boldsymbol{{mod}}\:\boldsymbol{{of}}\:\mid\mathrm{6}.\mathrm{23}\mid=\mathrm{6}.\mathrm{23} \\ $$$$\boldsymbol{{when}}\:\boldsymbol{{a}}=−\sqrt{\mathrm{2}}\: \\ $$$$=\frac{−\sqrt{\mathrm{2}}}{\mathrm{1}}+\frac{\mathrm{2}}{−\sqrt{\mathrm{2}}\:−\mathrm{1}} \\ $$$$=\frac{−\sqrt{\mathrm{2}}}{\mathrm{1}}−\frac{\mathrm{2}\left(\sqrt{\mathrm{2}}\:−\mathrm{1}\right)}{\left(\sqrt{\mathrm{2}}\:+\mathrm{1}\right)\left(\sqrt{\mathrm{2}}\:−\mathrm{1}\right)} \\ $$$$=−\sqrt{\mathrm{2}}\:−\mathrm{2}\sqrt{\mathrm{2}}\:+\mathrm{2} \\ $$$$=\mathrm{2}−\mathrm{3}\sqrt{\mathrm{2}}\: \\ $$$$=−\mathrm{2}.\mathrm{23} \\ $$$$\boldsymbol{{so}}\:\boldsymbol{{mod}}\:\boldsymbol{{of}}\:−\mathrm{2}.\mathrm{23}\:\mid−\mathrm{2}.\mathrm{23}\mid=\mathrm{2}.\mathrm{23} \\ $$$${hence}\:{minimum}\:{value}=\mathrm{2}.\mathrm{23} \\ $$
