Menu Close

Question-65729

Tinku Tara
Pin




Question Number 65729 by aliesam last updated on 02/Aug/19
Commented by mathmax by abdo last updated on 03/Aug/19
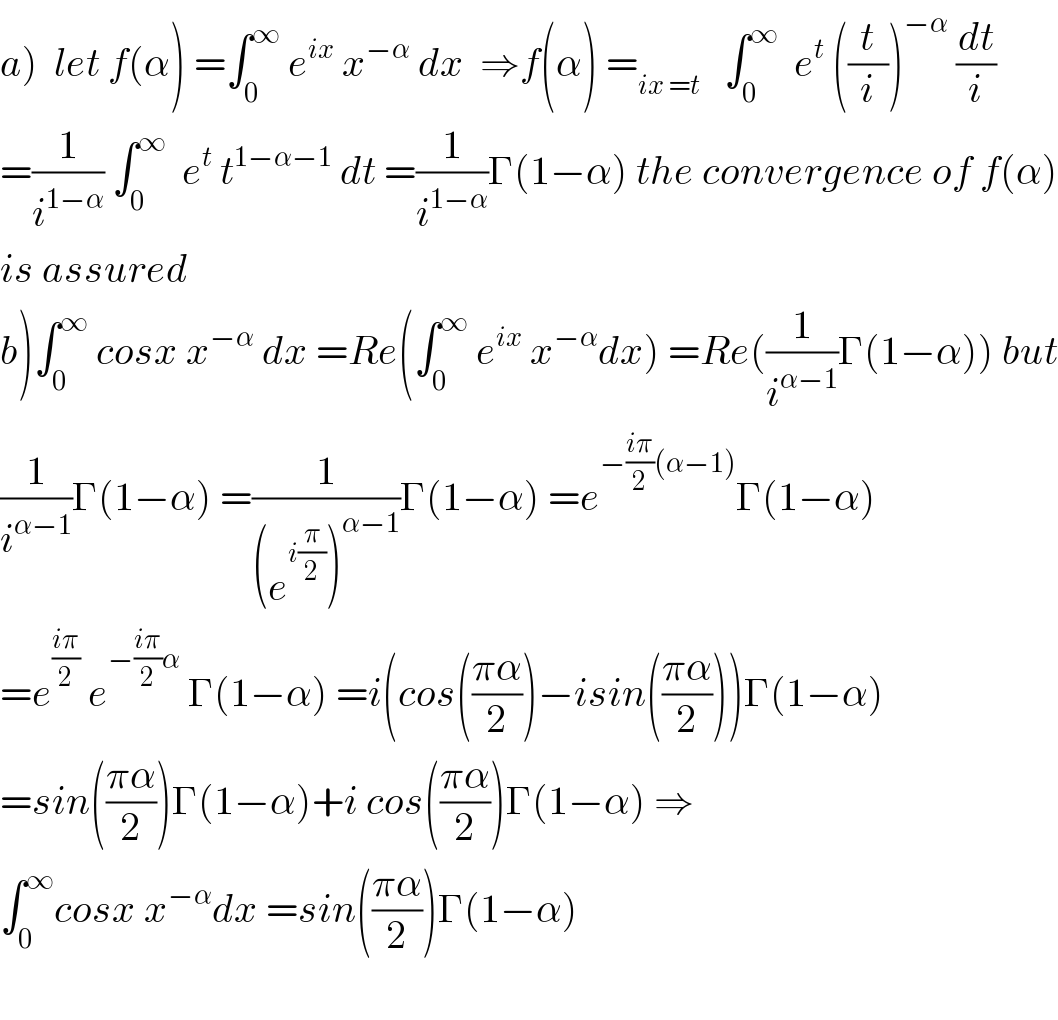
a) let f(α) =∫_0 ^∞ e^(ix) x^(−α) dx ⇒f(α) =_(ix =t) ∫_0 ^∞ e^t ((t/i))^(−α) (dt/i) =(1/i^(1−α) ) ∫_0 ^∞ e^t t^(1−α−1) dt =(1/i^(1−α) )Γ(1−α) the convergence of f(α) is assured b)∫_0 ^∞ cosx x^(−α) dx =Re(∫_0 ^∞ e^(ix) x^(−α) dx) =Re((1/i^(α−1) )Γ(1−α)) but (1/i^(α−1) )Γ(1−α) =(1/((e^(i(π/2)) )^(α−1) ))Γ(1−α) =e^(−((iπ)/2)(α−1)) Γ(1−α) =e^((iπ)/2) e^(−((iπ)/2)α) Γ(1−α) =i(cos(((πα)/2))−isin(((πα)/2)))Γ(1−α) =sin(((πα)/2))Γ(1−α)+i cos(((πα)/2))Γ(1−α) ⇒ ∫_0 ^∞ cosx x^(−α) dx =sin(((πα)/2))Γ(1−α)
$$\left.{a}\right)\:\:{let}\:{f}\left(\alpha\right)\:=\int_{\mathrm{0}} ^{\infty} \:{e}^{{ix}} \:{x}^{−\alpha} \:{dx}\:\:\Rightarrow{f}\left(\alpha\right)\:=_{{ix}\:={t}} \:\:\:\int_{\mathrm{0}} ^{\infty} \:\:{e}^{{t}} \:\left(\frac{{t}}{{i}}\right)^{−\alpha} \:\frac{{dt}}{{i}} \\ $$$$=\frac{\mathrm{1}}{{i}^{\mathrm{1}−\alpha} }\:\int_{\mathrm{0}} ^{\infty} \:\:{e}^{{t}} \:{t}^{\mathrm{1}−\alpha−\mathrm{1}} \:{dt}\:=\frac{\mathrm{1}}{{i}^{\mathrm{1}−\alpha} }\Gamma\left(\mathrm{1}−\alpha\right)\:{the}\:{convergence}\:{of}\:{f}\left(\alpha\right) \\ $$$${is}\:{assured} \\ $$$$\left.{b}\right)\int_{\mathrm{0}} ^{\infty} \:{cosx}\:{x}^{−\alpha} \:{dx}\:={Re}\left(\int_{\mathrm{0}} ^{\infty} \:{e}^{{ix}} \:{x}^{−\alpha} {dx}\right)\:={Re}\left(\frac{\mathrm{1}}{{i}^{\alpha−\mathrm{1}} }\Gamma\left(\mathrm{1}−\alpha\right)\right)\:{but} \\ $$$$\frac{\mathrm{1}}{{i}^{\alpha−\mathrm{1}} }\Gamma\left(\mathrm{1}−\alpha\right)\:=\frac{\mathrm{1}}{\left({e}^{{i}\frac{\pi}{\mathrm{2}}} \right)^{\alpha−\mathrm{1}} }\Gamma\left(\mathrm{1}−\alpha\right)\:={e}^{−\frac{{i}\pi}{\mathrm{2}}\left(\alpha−\mathrm{1}\right)} \Gamma\left(\mathrm{1}−\alpha\right) \\ $$$$={e}^{\frac{{i}\pi}{\mathrm{2}}} \:{e}^{−\frac{{i}\pi}{\mathrm{2}}\alpha} \:\Gamma\left(\mathrm{1}−\alpha\right)\:={i}\left({cos}\left(\frac{\pi\alpha}{\mathrm{2}}\right)−{isin}\left(\frac{\pi\alpha}{\mathrm{2}}\right)\right)\Gamma\left(\mathrm{1}−\alpha\right) \\ $$$$={sin}\left(\frac{\pi\alpha}{\mathrm{2}}\right)\Gamma\left(\mathrm{1}−\alpha\right)+{i}\:{cos}\left(\frac{\pi\alpha}{\mathrm{2}}\right)\Gamma\left(\mathrm{1}−\alpha\right)\:\Rightarrow \\ $$$$\int_{\mathrm{0}} ^{\infty} {cosx}\:{x}^{−\alpha} {dx}\:={sin}\left(\frac{\pi\alpha}{\mathrm{2}}\right)\Gamma\left(\mathrm{1}−\alpha\right) \\ $$$$ \\ $$
Commented by aliesam last updated on 03/Aug/19
thank you sir.but the first question ineed to prove the integral is ineed convergent before computing its value concerning .the second question,i meant by complex integration is by using the residue theorem
$${thank}\:{you}\:{sir}.{but}\:{the}\:{first}\:{question} \\ $$$$\:{ineed}\:{to}\:{prove}\:{the}\:{integral}\:{is}\:{ineed} \\ $$$${convergent}\:{before}\:{computing}\:{its}\:{value} \\ $$$${concerning}\:.{the}\:{second}\:{question},{i}\:{meant}\:{by}\:{complex}\:{integration} \\ $$$${is}\:{by}\:{using}\:{the}\:{residue}\:{theorem} \\ $$$$ \\ $$
Commented by aliesam last updated on 04/Aug/19

Pin