Menu Close

Question-65740

Tinku Tara
Pin




Question Number 65740 by rajesh4661kumar@gmail.com last updated on 03/Aug/19
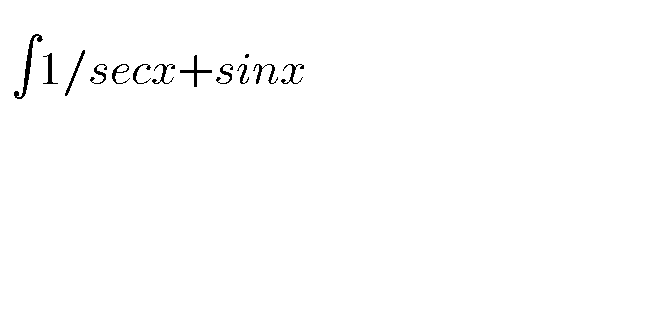
Commented by mathmax by abdo last updated on 03/Aug/19
let A = ∫ (dx/((1/(cosx)) +sinx)) ⇒ A =∫ ((cosx)/(1+cosx sinx))dx changement tan((x/(2 ))) =t give A =∫ (((1−t^2 )/(1+t^2 ))/(1+((2t(1−t^2 ))/((1+t^2 )^2 )))) ((2dt)/(1+t^2 )) = ∫ ((1−t^2 )/((1+t^2 )^2 {1+((2t(1−t^2 ))/((1+t^2 )^2 ))}))dt =∫ ((1−t^2 )/((1+t^2 )^2 +2t(1−t^2 )))dt =∫ ((1−t^2 )/(t^4 +2t^2 +1 +2t−2t^3 ))dt =∫ ((1−t^2 )/(t^4 −2t^3 +2t +1))dt let decompose F(t) =((1−t^2 )/(t^4 −2t^3 +2t +1)) t^4 −2t^3 +2t +1 =0 the roots are z_1 =1,5291 +0,7429i =α+iβ z_2 =1,5291−0,7429 i (=z_1 ^− ) =α−iβ z_3 =−0,5291 +0,2571i =−α+iλ z_4 =−0,5291 −0,2571 i(=z_3 ^− ) =−α−iλ ⇒F(t)=((1−t^2 )/((t−z_1 )(t−z_1 ^− )(t−z_3 )(t−z_3 ^− ))) =((1−t^2 )/((t^2 −2Re(z_1 )t +∣z_1 ∣^2 )(t^2 −2Re(z_3 )t +∣z_3 ^2 ∣))) =((1−t^2 )/((t^2 −2αt +α^2 +β^2 )(t^2 +2αt +α^2 +λ^2 ))) =((at +b)/(t^2 −2αt +α^2 +β^2 )) +((ct +d)/(t^2 +2αt +α^2 +λ^2 )) ....be continued...
$${let}\:{A}\:=\:\int\:\:\:\frac{{dx}}{\frac{\mathrm{1}}{{cosx}}\:+{sinx}}\:\Rightarrow\:{A}\:=\int\:\frac{{cosx}}{\mathrm{1}+{cosx}\:{sinx}}{dx}\:{changement} \\ $$$${tan}\left(\frac{{x}}{\mathrm{2}\:}\right)\:={t}\:{give}\:{A}\:=\int\:\:\:\frac{\frac{\mathrm{1}−{t}^{\mathrm{2}} }{\mathrm{1}+{t}^{\mathrm{2}} }}{\mathrm{1}+\frac{\mathrm{2}{t}\left(\mathrm{1}−{t}^{\mathrm{2}} \right)}{\left(\mathrm{1}+{t}^{\mathrm{2}} \right)^{\mathrm{2}} }}\:\frac{\mathrm{2}{dt}}{\mathrm{1}+{t}^{\mathrm{2}} } \\ $$$$=\:\int\:\:\:\frac{\mathrm{1}−{t}^{\mathrm{2}} }{\left(\mathrm{1}+{t}^{\mathrm{2}} \right)^{\mathrm{2}} \left\{\mathrm{1}+\frac{\mathrm{2}{t}\left(\mathrm{1}−{t}^{\mathrm{2}} \right)}{\left(\mathrm{1}+{t}^{\mathrm{2}} \right)^{\mathrm{2}} }\right\}}{dt}\:=\int\:\:\:\frac{\mathrm{1}−{t}^{\mathrm{2}} }{\left(\mathrm{1}+{t}^{\mathrm{2}} \right)^{\mathrm{2}} \:+\mathrm{2}{t}\left(\mathrm{1}−{t}^{\mathrm{2}} \right)}{dt} \\ $$$$=\int\:\:\:\frac{\mathrm{1}−{t}^{\mathrm{2}} }{{t}^{\mathrm{4}} \:+\mathrm{2}{t}^{\mathrm{2}} +\mathrm{1}\:+\mathrm{2}{t}−\mathrm{2}{t}^{\mathrm{3}} }{dt}\:=\int\:\:\frac{\mathrm{1}−{t}^{\mathrm{2}} }{{t}^{\mathrm{4}} −\mathrm{2}{t}^{\mathrm{3}} +\mathrm{2}{t}\:+\mathrm{1}}{dt} \\ $$$${let}\:{decompose}\:{F}\left({t}\right)\:=\frac{\mathrm{1}−{t}^{\mathrm{2}} }{{t}^{\mathrm{4}} −\mathrm{2}{t}^{\mathrm{3}} \:+\mathrm{2}{t}\:+\mathrm{1}} \\ $$$${t}^{\mathrm{4}} −\mathrm{2}{t}^{\mathrm{3}} \:+\mathrm{2}{t}\:+\mathrm{1}\:=\mathrm{0}\:\:{the}\:{roots}\:{are} \\ $$$${z}_{\mathrm{1}} =\mathrm{1},\mathrm{5291}\:+\mathrm{0},\mathrm{7429}{i}\:\:=\alpha+{i}\beta \\ $$$${z}_{\mathrm{2}} =\mathrm{1},\mathrm{5291}−\mathrm{0},\mathrm{7429}\:{i}\:\left(=\overset{−} {{z}}_{\mathrm{1}} \right)\:=\alpha−{i}\beta \\ $$$${z}_{\mathrm{3}} =−\mathrm{0},\mathrm{5291}\:+\mathrm{0},\mathrm{2571}{i}\:=−\alpha+{i}\lambda \\ $$$${z}_{\mathrm{4}} =−\mathrm{0},\mathrm{5291}\:−\mathrm{0},\mathrm{2571}\:{i}\left(=\overset{−} {{z}}_{\mathrm{3}} \right)\:=−\alpha−{i}\lambda \\ $$$$\Rightarrow{F}\left({t}\right)=\frac{\mathrm{1}−{t}^{\mathrm{2}} }{\left({t}−{z}_{\mathrm{1}} \right)\left({t}−\overset{−} {{z}}_{\mathrm{1}} \right)\left({t}−{z}_{\mathrm{3}} \right)\left({t}−\overset{−} {{z}}_{\mathrm{3}} \right)} \\ $$$$=\frac{\mathrm{1}−{t}^{\mathrm{2}} }{\left({t}^{\mathrm{2}} −\mathrm{2}{Re}\left({z}_{\mathrm{1}} \right){t}\:+\mid{z}_{\mathrm{1}} \mid^{\mathrm{2}} \right)\left({t}^{\mathrm{2}} −\mathrm{2}{Re}\left({z}_{\mathrm{3}} \right){t}\:+\mid{z}_{\mathrm{3}} ^{\mathrm{2}} \mid\right)} \\ $$$$=\frac{\mathrm{1}−{t}^{\mathrm{2}} }{\left({t}^{\mathrm{2}} −\mathrm{2}\alpha{t}\:\:+\alpha^{\mathrm{2}} \:+\beta^{\mathrm{2}} \right)\left({t}^{\mathrm{2}} +\mathrm{2}\alpha{t}\:+\alpha^{\mathrm{2}} \:+\lambda^{\mathrm{2}} \right)} \\ $$$$=\frac{{at}\:+{b}}{{t}^{\mathrm{2}} −\mathrm{2}\alpha{t}\:+\alpha^{\mathrm{2}} \:+\beta^{\mathrm{2}} }\:+\frac{{ct}\:+{d}}{{t}^{\mathrm{2}} \:+\mathrm{2}\alpha{t}\:+\alpha^{\mathrm{2}} \:+\lambda^{\mathrm{2}} }\:….{be}\:{continued}… \\ $$

Pin