Question Number 65749 by bshahid010@gmail.com last updated on 03/Aug/19

Answered by Tanmay chaudhury last updated on 03/Aug/19
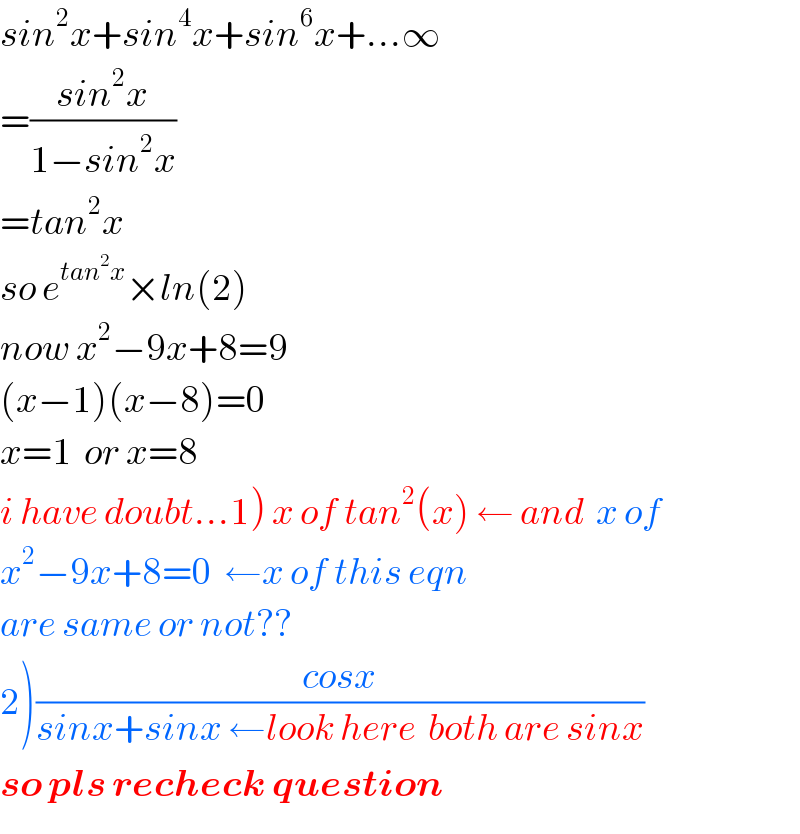
$${sin}^{\mathrm{2}} {x}+{sin}^{\mathrm{4}} {x}+{sin}^{\mathrm{6}} {x}+…\infty \\ $$$$=\frac{{sin}^{\mathrm{2}} {x}}{\mathrm{1}−{sin}^{\mathrm{2}} {x}} \\ $$$$={tan}^{\mathrm{2}} {x} \\ $$$${so}\:{e}^{{tan}^{\mathrm{2}} {x}} ×{ln}\left(\mathrm{2}\right) \\ $$$${now}\:{x}^{\mathrm{2}} −\mathrm{9}{x}+\mathrm{8}=\mathrm{9} \\ $$$$\left({x}−\mathrm{1}\right)\left({x}−\mathrm{8}\right)=\mathrm{0} \\ $$$${x}=\mathrm{1}\:\:{or}\:{x}=\mathrm{8} \\ $$$$\left.{i}\:{have}\:{doubt}…\mathrm{1}\right)\:{x}\:{of}\:{tan}^{\mathrm{2}} \left({x}\right)\:\leftarrow\:{and}\:\:{x}\:{of}\: \\ $$$${x}^{\mathrm{2}} −\mathrm{9}{x}+\mathrm{8}=\mathrm{0}\:\:\leftarrow{x}\:{of}\:{this}\:{eqn}\: \\ $$$${are}\:{same}\:{or}\:{not}?? \\ $$$$\left.\mathrm{2}\right)\frac{{cosx}}{{sinx}+{sinx}\:\leftarrow{look}\:{here}\:\:{both}\:{are}\:{sinx}} \\ $$$$\boldsymbol{{so}}\:\boldsymbol{{pls}}\:\boldsymbol{{recheck}}\:\boldsymbol{{question}} \\ $$
