Menu Close

Question-65884

Tinku Tara
Pin




Question Number 65884 by Sayantan chakraborty last updated on 05/Aug/19
Commented by Sayantan chakraborty last updated on 05/Aug/19
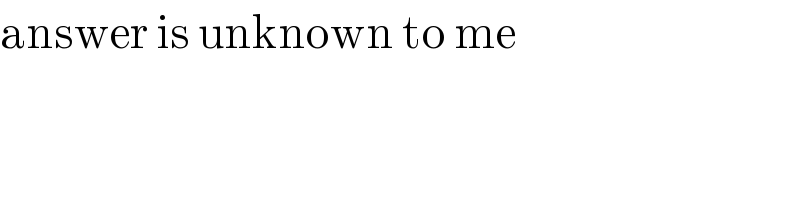
answer is unknown to me
$$\mathrm{answer}\:\mathrm{is}\:\mathrm{unknown}\:\mathrm{to}\:\mathrm{me} \\ $$
Commented by Tony Lin last updated on 06/Aug/19
let∠BAD=∠BCD=θ, ∠BDA=∅ (5/(sin∅))=((6sinθ)/(sinθ))=6 ⇒sin∅=(5/6), cos∅=−((√(11))/6) 2(DM^2 +AM^2 )=DC^2 +AD^2 DC^2 =(6cosθ)^2 =36cos^2 θ ((AD)/(sin(180°−θ−∅)))=((6sinθ)/(sinθ))=6 AD=6sin(θ+∅)=5cosθ−(√(11))sinθ AD^2 =25cos^2 θ−10(√(11))sinθcosθ+11sin^2 θ AC^2 =5^2 +6^2 −2×5×6cos(270°−2θ−∅) =61+60sin(2θ+∅) =61+60[2sinθcosθcos∅+(1−2sin^2 θ)sin∅] =61−20(√(11))sinθcosθ+50−100sin^2 θ AM^2 =((61)/4)−5(√(11))sinθcosθ+((25)/2)−25sin^2 θ 2(DM^2 +AM^2 )=DC^2 +AD^2 2DM^2 +((61)/2)−10(√(11))sinθcosθ+25−50sin^2 θ =36cos^2 θ+25cos^2 θ−10(√(11))sinθcosθ+11sin^2 θ 2DM^2 +((61)/2)+25=61(sin^2 θ+cos^2 θ) DM^2 =((11)/4)⇒DM=((√(11))/2)=((√a)/2) ⇒a=11
$${let}\angle{BAD}=\angle{BCD}=\theta,\:\angle{BDA}=\emptyset \\ $$$$\frac{\mathrm{5}}{{sin}\emptyset}=\frac{\mathrm{6}{sin}\theta}{{sin}\theta}=\mathrm{6} \\ $$$$\Rightarrow{sin}\emptyset=\frac{\mathrm{5}}{\mathrm{6}},\:{cos}\emptyset=−\frac{\sqrt{\mathrm{11}}}{\mathrm{6}} \\ $$$$\mathrm{2}\left({DM}^{\mathrm{2}} +{AM}^{\mathrm{2}} \right)={DC}^{\mathrm{2}} +{AD}^{\mathrm{2}} \\ $$$${DC}^{\mathrm{2}} =\left(\mathrm{6}{cos}\theta\right)^{\mathrm{2}} =\mathrm{36}{cos}^{\mathrm{2}} \theta \\ $$$$\frac{{AD}}{{sin}\left(\mathrm{180}°−\theta−\emptyset\right)}=\frac{\mathrm{6}{sin}\theta}{{sin}\theta}=\mathrm{6} \\ $$$${AD}=\mathrm{6}{sin}\left(\theta+\emptyset\right)=\mathrm{5}{cos}\theta−\sqrt{\mathrm{11}}{sin}\theta \\ $$$${AD}^{\mathrm{2}} =\mathrm{25}{cos}^{\mathrm{2}} \theta−\mathrm{10}\sqrt{\mathrm{11}}{sin}\theta{cos}\theta+\mathrm{11}{sin}^{\mathrm{2}} \theta \\ $$$${AC}^{\mathrm{2}} =\mathrm{5}^{\mathrm{2}} +\mathrm{6}^{\mathrm{2}} −\mathrm{2}×\mathrm{5}×\mathrm{6}{cos}\left(\mathrm{270}°−\mathrm{2}\theta−\emptyset\right) \\ $$$$=\mathrm{61}+\mathrm{60}{sin}\left(\mathrm{2}\theta+\emptyset\right) \\ $$$$=\mathrm{61}+\mathrm{60}\left[\mathrm{2}{sin}\theta{cos}\theta{cos}\emptyset+\left(\mathrm{1}−\mathrm{2}{sin}^{\mathrm{2}} \theta\right){sin}\emptyset\right] \\ $$$$=\mathrm{61}−\mathrm{20}\sqrt{\mathrm{11}}{sin}\theta{cos}\theta+\mathrm{50}−\mathrm{100}{sin}^{\mathrm{2}} \theta \\ $$$${AM}^{\mathrm{2}} =\frac{\mathrm{61}}{\mathrm{4}}−\mathrm{5}\sqrt{\mathrm{11}}{sin}\theta{cos}\theta+\frac{\mathrm{25}}{\mathrm{2}}−\mathrm{25}{sin}^{\mathrm{2}} \theta \\ $$$$\mathrm{2}\left({DM}^{\mathrm{2}} +{AM}^{\mathrm{2}} \right)={DC}^{\mathrm{2}} +{AD}^{\mathrm{2}} \\ $$$$\mathrm{2}{DM}^{\mathrm{2}} +\frac{\mathrm{61}}{\mathrm{2}}−\mathrm{10}\sqrt{\mathrm{11}}{sin}\theta{cos}\theta+\mathrm{25}−\mathrm{50}{sin}^{\mathrm{2}} \theta \\ $$$$=\mathrm{36}{cos}^{\mathrm{2}} \theta+\mathrm{25}{cos}^{\mathrm{2}} \theta−\mathrm{10}\sqrt{\mathrm{11}}{sin}\theta{cos}\theta+\mathrm{11}{sin}^{\mathrm{2}} \theta \\ $$$$\mathrm{2}{DM}^{\mathrm{2}} +\frac{\mathrm{61}}{\mathrm{2}}+\mathrm{25}=\mathrm{61}\left({sin}^{\mathrm{2}} \theta+{cos}^{\mathrm{2}} \theta\right) \\ $$$${DM}^{\mathrm{2}} =\frac{\mathrm{11}}{\mathrm{4}}\Rightarrow{DM}=\frac{\sqrt{\mathrm{11}}}{\mathrm{2}}=\frac{\sqrt{{a}}}{\mathrm{2}} \\ $$$$\Rightarrow{a}=\mathrm{11} \\ $$
Commented by Sayantan chakraborty last updated on 17/Aug/19
sir please solve question number 65886
$$\boldsymbol{\mathrm{sir}}\:\boldsymbol{\mathrm{please}}\:\boldsymbol{\mathrm{solve}}\:\boldsymbol{\mathrm{question}}\:\boldsymbol{\mathrm{number}}\:\mathrm{65886} \\ $$

Pin