Question Number 65981 by Tanmay chaudhury last updated on 07/Aug/19

Answered by jimful last updated on 07/Aug/19
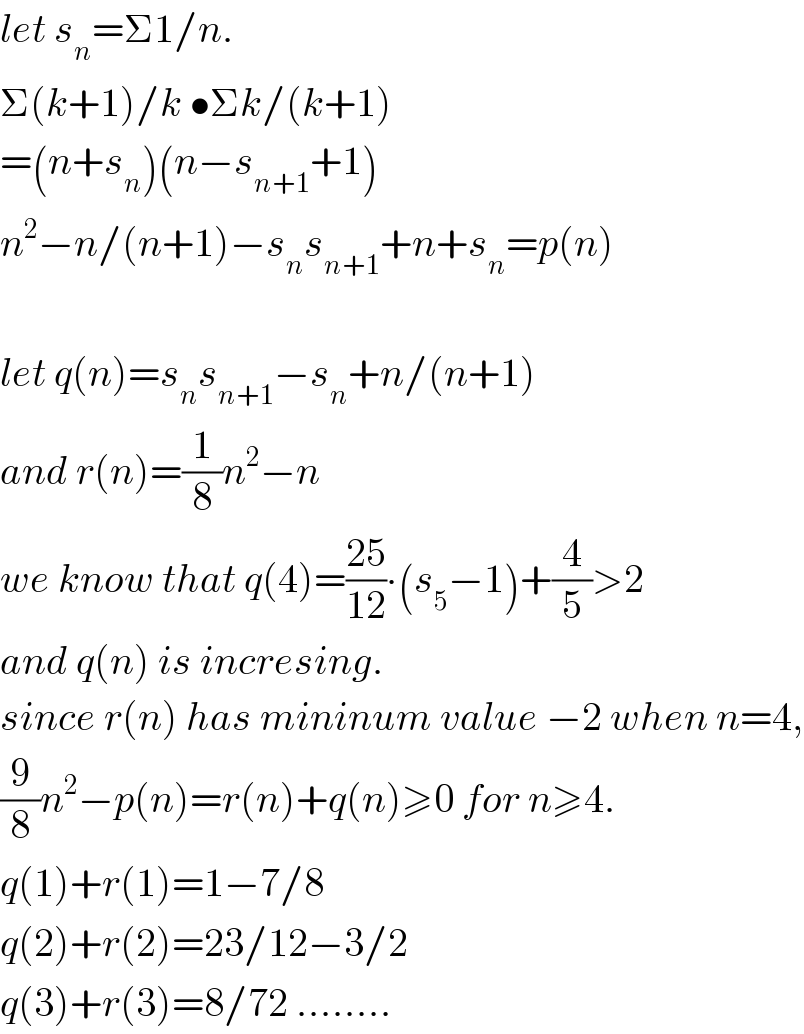
$${let}\:{s}_{{n}} =\Sigma\mathrm{1}/{n}. \\ $$$$\Sigma\left({k}+\mathrm{1}\right)/{k}\:\bullet\Sigma{k}/\left({k}+\mathrm{1}\right) \\ $$$$=\left({n}+{s}_{{n}} \right)\left({n}−{s}_{{n}+\mathrm{1}} +\mathrm{1}\right) \\ $$$${n}^{\mathrm{2}} −{n}/\left({n}+\mathrm{1}\right)−{s}_{{n}} {s}_{{n}+\mathrm{1}} +{n}+{s}_{{n}} ={p}\left({n}\right) \\ $$$$ \\ $$$${let}\:{q}\left({n}\right)={s}_{{n}} {s}_{{n}+\mathrm{1}} −{s}_{{n}} +{n}/\left({n}+\mathrm{1}\right) \\ $$$${and}\:{r}\left({n}\right)=\frac{\mathrm{1}}{\mathrm{8}}{n}^{\mathrm{2}} −{n} \\ $$$${we}\:{know}\:{that}\:{q}\left(\mathrm{4}\right)=\frac{\mathrm{25}}{\mathrm{12}}\centerdot\left({s}_{\mathrm{5}} −\mathrm{1}\right)+\frac{\mathrm{4}}{\mathrm{5}}>\mathrm{2} \\ $$$${and}\:{q}\left({n}\right)\:{is}\:{incresing}. \\ $$$${since}\:{r}\left({n}\right)\:{has}\:{mininum}\:{value}\:−\mathrm{2}\:{when}\:{n}=\mathrm{4}, \\ $$$$\frac{\mathrm{9}}{\mathrm{8}}{n}^{\mathrm{2}} −{p}\left({n}\right)={r}\left({n}\right)+{q}\left({n}\right)\geqslant\mathrm{0}\:{for}\:{n}\geqslant\mathrm{4}. \\ $$$${q}\left(\mathrm{1}\right)+{r}\left(\mathrm{1}\right)=\mathrm{1}−\mathrm{7}/\mathrm{8} \\ $$$${q}\left(\mathrm{2}\right)+{r}\left(\mathrm{2}\right)=\mathrm{23}/\mathrm{12}−\mathrm{3}/\mathrm{2} \\ $$$${q}\left(\mathrm{3}\right)+{r}\left(\mathrm{3}\right)=\mathrm{8}/\mathrm{72}\:…….. \\ $$
Commented by Tanmay chaudhury last updated on 07/Aug/19

$${thank}\:{you}\:{sir} \\ $$
