Question-66082

Question Number 66082 by aliesam last updated on 08/Aug/19

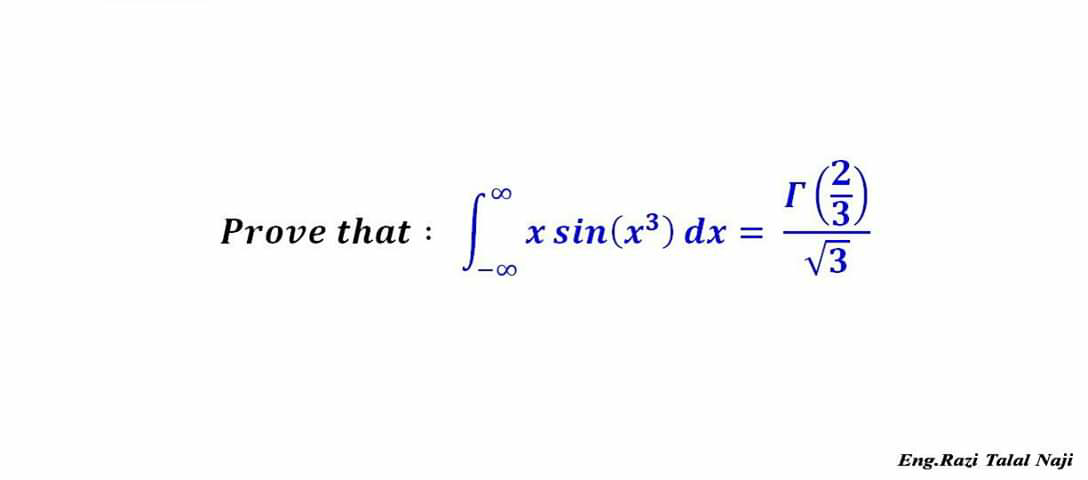
Commented by mathmax by abdo last updated on 09/Aug/19

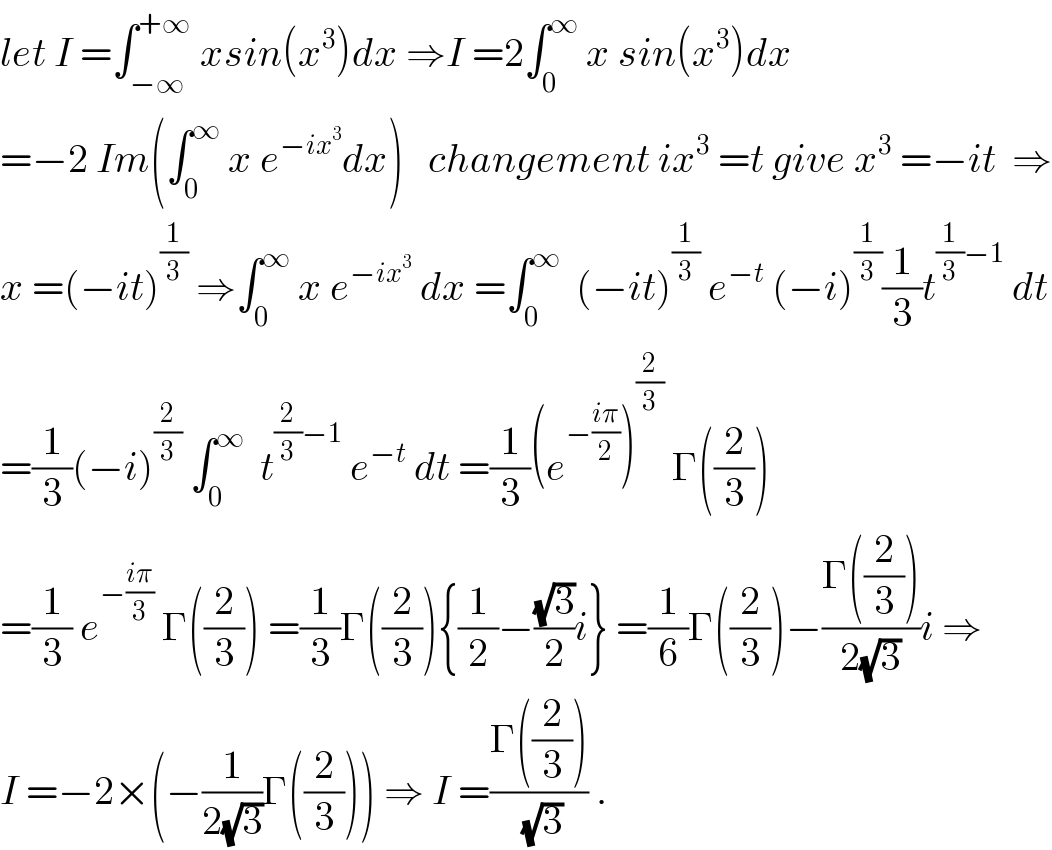
let I =∫_(−∞) ^(+∞) xsin(x^3 )dx ⇒I =2∫_0 ^∞ x sin(x^3 )dx =−2 Im(∫_0 ^∞ x e^(−ix^3 ) dx) changement ix^3 =t give x^3 =−it ⇒ x =(−it)^(1/3) ⇒∫_0 ^∞ x e^(−ix^3 ) dx =∫_0 ^∞ (−it)^(1/3) e^(−t) (−i)^(1/3) (1/3)t^((1/3)−1) dt =(1/3)(−i)^(2/3) ∫_0 ^∞ t^((2/3)−1) e^(−t) dt =(1/3)(e^(−((iπ)/2)) )^(2/3) Γ((2/3)) =(1/3) e^(−((iπ)/3)) Γ((2/3)) =(1/3)Γ((2/3)){(1/2)−((√3)/2)i} =(1/6)Γ((2/3))−((Γ((2/3)))/(2(√3)))i ⇒ I =−2×(−(1/(2(√3)))Γ((2/3))) ⇒ I =((Γ((2/3)))/( (√3))) .

$${let}\:{I}\:=\int_{−\infty} ^{+\infty} \:{xsin}\left({x}^{\mathrm{3}} \right){dx}\:\Rightarrow{I}\:=\mathrm{2}\int_{\mathrm{0}} ^{\infty} \:{x}\:{sin}\left({x}^{\mathrm{3}} \right){dx} \\ $$$$=−\mathrm{2}\:{Im}\left(\int_{\mathrm{0}} ^{\infty} \:{x}\:{e}^{−{ix}^{\mathrm{3}} } {dx}\right)\:\:\:{changement}\:{ix}^{\mathrm{3}} \:={t}\:{give}\:{x}^{\mathrm{3}} \:=−{it}\:\:\Rightarrow \\ $$$${x}\:=\left(−{it}\right)^{\frac{\mathrm{1}}{\mathrm{3}}} \:\Rightarrow\int_{\mathrm{0}} ^{\infty} \:{x}\:{e}^{−{ix}^{\mathrm{3}} } \:{dx}\:=\int_{\mathrm{0}} ^{\infty} \:\:\left(−{it}\right)^{\frac{\mathrm{1}}{\mathrm{3}}} \:{e}^{−{t}} \:\left(−{i}\right)^{\frac{\mathrm{1}}{\mathrm{3}}} \frac{\mathrm{1}}{\mathrm{3}}{t}^{\frac{\mathrm{1}}{\mathrm{3}}−\mathrm{1}} \:{dt} \\ $$$$=\frac{\mathrm{1}}{\mathrm{3}}\left(−{i}\right)^{\frac{\mathrm{2}}{\mathrm{3}}} \:\int_{\mathrm{0}} ^{\infty} \:\:{t}^{\frac{\mathrm{2}}{\mathrm{3}}−\mathrm{1}} \:{e}^{−{t}} \:{dt}\:=\frac{\mathrm{1}}{\mathrm{3}}\left({e}^{−\frac{{i}\pi}{\mathrm{2}}} \right)^{\frac{\mathrm{2}}{\mathrm{3}}} \:\Gamma\left(\frac{\mathrm{2}}{\mathrm{3}}\right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{3}}\:{e}^{−\frac{{i}\pi}{\mathrm{3}}} \:\Gamma\left(\frac{\mathrm{2}}{\mathrm{3}}\right)\:=\frac{\mathrm{1}}{\mathrm{3}}\Gamma\left(\frac{\mathrm{2}}{\mathrm{3}}\right)\left\{\frac{\mathrm{1}}{\mathrm{2}}−\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}{i}\right\}\:=\frac{\mathrm{1}}{\mathrm{6}}\Gamma\left(\frac{\mathrm{2}}{\mathrm{3}}\right)−\frac{\Gamma\left(\frac{\mathrm{2}}{\mathrm{3}}\right)}{\mathrm{2}\sqrt{\mathrm{3}}}{i}\:\Rightarrow \\ $$$${I}\:=−\mathrm{2}×\left(−\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{3}}}\Gamma\left(\frac{\mathrm{2}}{\mathrm{3}}\right)\right)\:\Rightarrow\:{I}\:=\frac{\Gamma\left(\frac{\mathrm{2}}{\mathrm{3}}\right)}{\:\sqrt{\mathrm{3}}}\:. \\ $$

Commented by aliesam last updated on 09/Aug/19

$${god}\:{bless}\:{you} \\ $$

Commented by mathmax by abdo last updated on 09/Aug/19

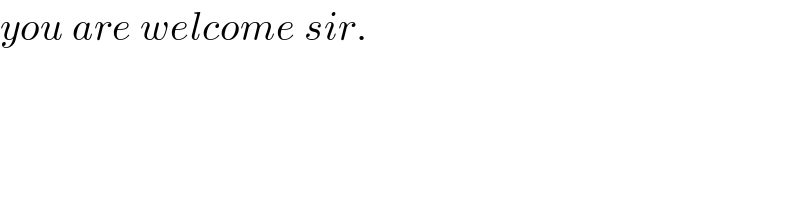
$${you}\:{are}\:{welcome}\:{sir}. \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply