Question Number 66498 by miracle wokama last updated on 16/Aug/19

Commented by MJS last updated on 16/Aug/19
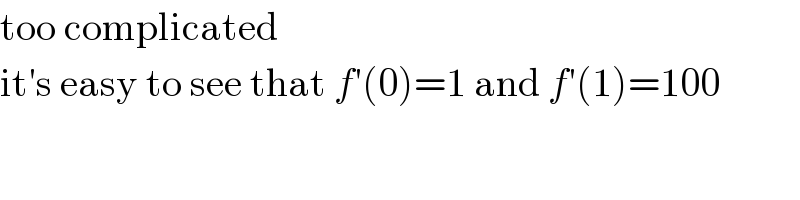
$$\mathrm{too}\:\mathrm{complicated} \\ $$$$\mathrm{it}'\mathrm{s}\:\mathrm{easy}\:\mathrm{to}\:\mathrm{see}\:\mathrm{that}\:{f}'\left(\mathrm{0}\right)=\mathrm{1}\:\mathrm{and}\:{f}'\left(\mathrm{1}\right)=\mathrm{100} \\ $$
Commented by mathmax by abdo last updated on 16/Aug/19
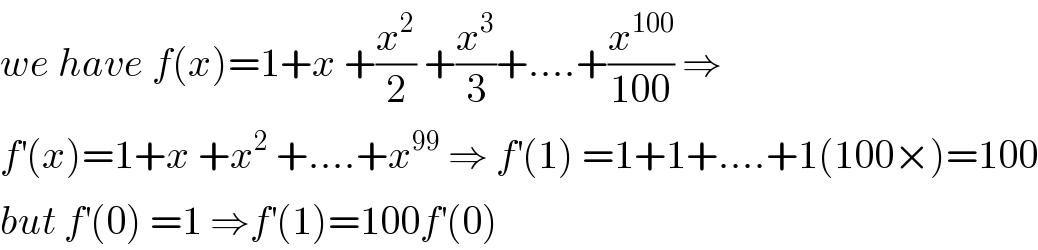
$${we}\:{have}\:{f}\left({x}\right)=\mathrm{1}+{x}\:+\frac{{x}^{\mathrm{2}} }{\mathrm{2}}\:+\frac{{x}^{\mathrm{3}} }{\mathrm{3}}+….+\frac{{x}^{\mathrm{100}} }{\mathrm{100}}\:\Rightarrow \\ $$$${f}^{'} \left({x}\right)=\mathrm{1}+{x}\:+{x}^{\mathrm{2}} \:+….+{x}^{\mathrm{99}} \:\Rightarrow\:{f}^{'} \left(\mathrm{1}\right)\:=\mathrm{1}+\mathrm{1}+….+\mathrm{1}\left(\mathrm{100}×\right)=\mathrm{100} \\ $$$${but}\:{f}^{'} \left(\mathrm{0}\right)\:=\mathrm{1}\:\Rightarrow{f}^{'} \left(\mathrm{1}\right)=\mathrm{100}{f}^{'} \left(\mathrm{0}\right) \\ $$
Commented by mathmax by abdo last updated on 16/Aug/19
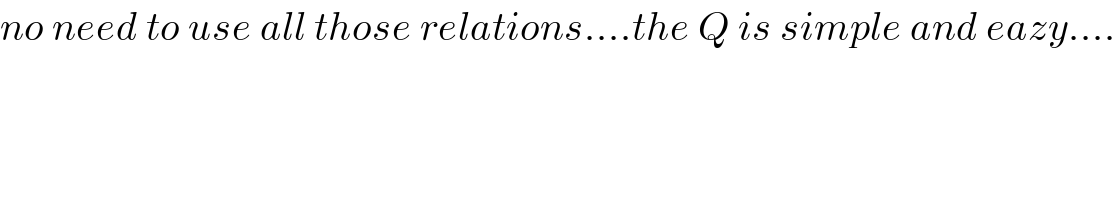
$${no}\:{need}\:{to}\:{use}\:{all}\:{those}\:{relations}….{the}\:{Q}\:{is}\:{simple}\:{and}\:{eazy}…. \\ $$
Answered by Cmr 237 last updated on 17/Aug/19
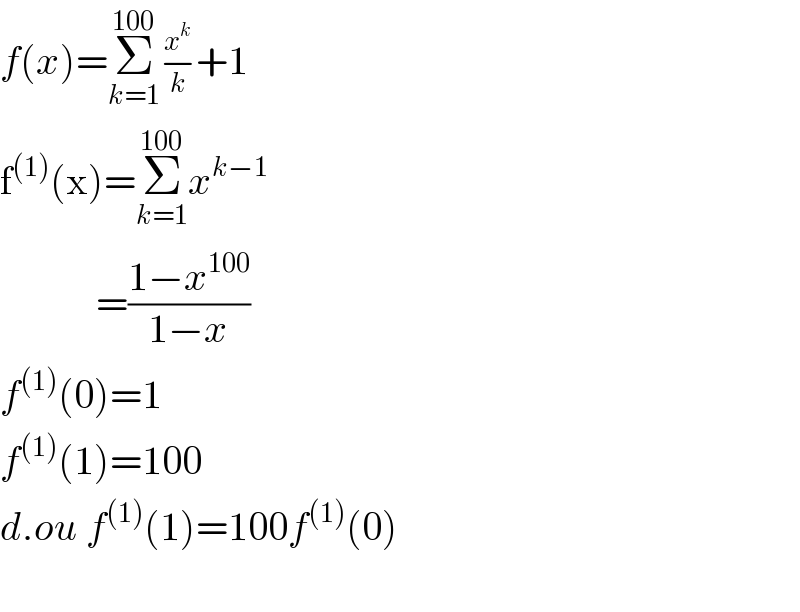
$${f}\left({x}\right)=\underset{{k}=\mathrm{1}} {\overset{\mathrm{100}} {\sum}}\underset{{k}} {\overset{{x}^{{k}} } {−}}+\mathrm{1} \\ $$$$\mathrm{f}^{\left(\mathrm{1}\right)} \left(\mathrm{x}\right)=\underset{{k}=\mathrm{1}} {\overset{\mathrm{100}} {\sum}}{x}^{{k}−\mathrm{1}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:=\frac{\mathrm{1}−{x}^{\mathrm{100}} }{\mathrm{1}−{x}} \\ $$$${f}^{\left(\mathrm{1}\right)} \left(\mathrm{0}\right)=\mathrm{1} \\ $$$${f}^{\left(\mathrm{1}\right)} \left(\mathrm{1}\right)=\mathrm{100} \\ $$$${d}.{ou}\:{f}^{\left(\mathrm{1}\right)} \left(\mathrm{1}\right)=\mathrm{100}{f}^{\left(\mathrm{1}\right)} \left(\mathrm{0}\right) \\ $$$$ \\ $$
