Question Number 66518 by Masumsiddiqui399@gmail.com last updated on 16/Aug/19
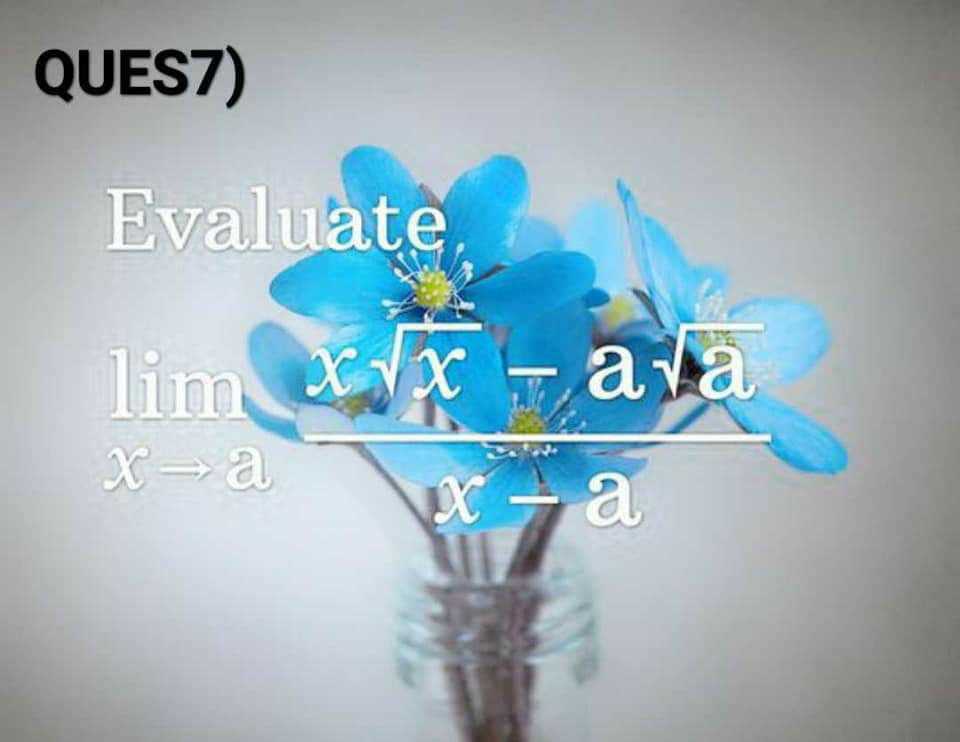
Commented by mathmax by abdo last updated on 16/Aug/19
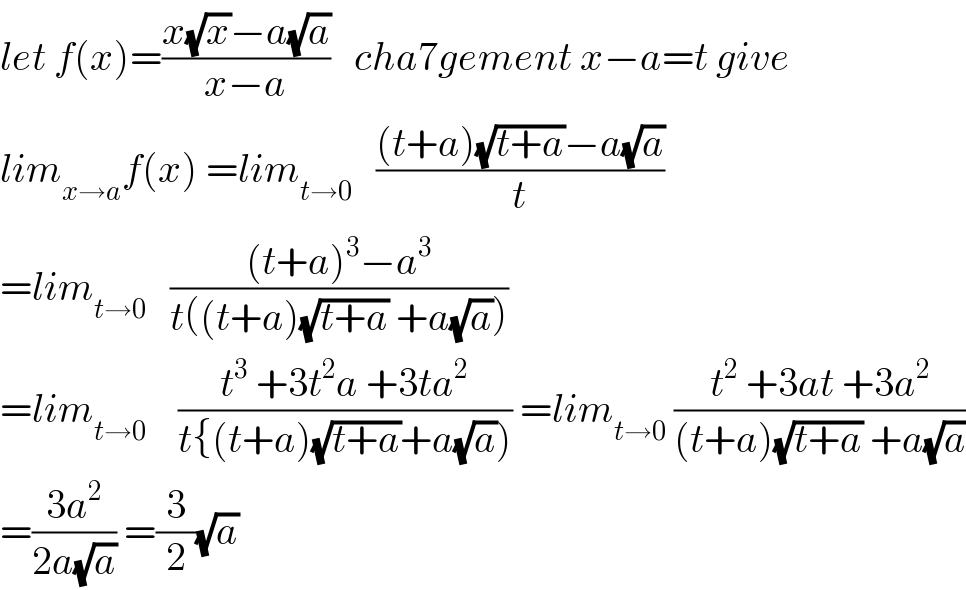
$${let}\:{f}\left({x}\right)=\frac{{x}\sqrt{{x}}−{a}\sqrt{{a}}}{{x}−{a}}\:\:\:{cha}\mathrm{7}{gement}\:{x}−{a}={t}\:{give} \\ $$$${lim}_{{x}\rightarrow{a}} {f}\left({x}\right)\:={lim}_{{t}\rightarrow\mathrm{0}} \:\:\:\frac{\left({t}+{a}\right)\sqrt{{t}+{a}}−{a}\sqrt{{a}}}{{t}} \\ $$$$={lim}_{{t}\rightarrow\mathrm{0}} \:\:\:\frac{\left({t}+{a}\right)^{\mathrm{3}} −{a}^{\mathrm{3}} }{{t}\left(\left({t}+{a}\right)\sqrt{{t}+{a}}\:+{a}\sqrt{{a}}\right)}\: \\ $$$$={lim}_{{t}\rightarrow\mathrm{0}} \:\:\:\:\frac{{t}^{\mathrm{3}} \:+\mathrm{3}{t}^{\mathrm{2}} {a}\:+\mathrm{3}{ta}^{\mathrm{2}} }{{t}\left\{\left({t}+{a}\right)\sqrt{{t}+{a}}+{a}\sqrt{{a}}\right)}\:={lim}_{{t}\rightarrow\mathrm{0}} \:\frac{{t}^{\mathrm{2}} \:+\mathrm{3}{at}\:+\mathrm{3}{a}^{\mathrm{2}} }{\left({t}+{a}\right)\sqrt{{t}+{a}}\:+{a}\sqrt{{a}}} \\ $$$$=\frac{\mathrm{3}{a}^{\mathrm{2}} }{\mathrm{2}{a}\sqrt{{a}}}\:=\frac{\mathrm{3}}{\mathrm{2}}\sqrt{{a}} \\ $$
Commented by Tony Lin last updated on 16/Aug/19
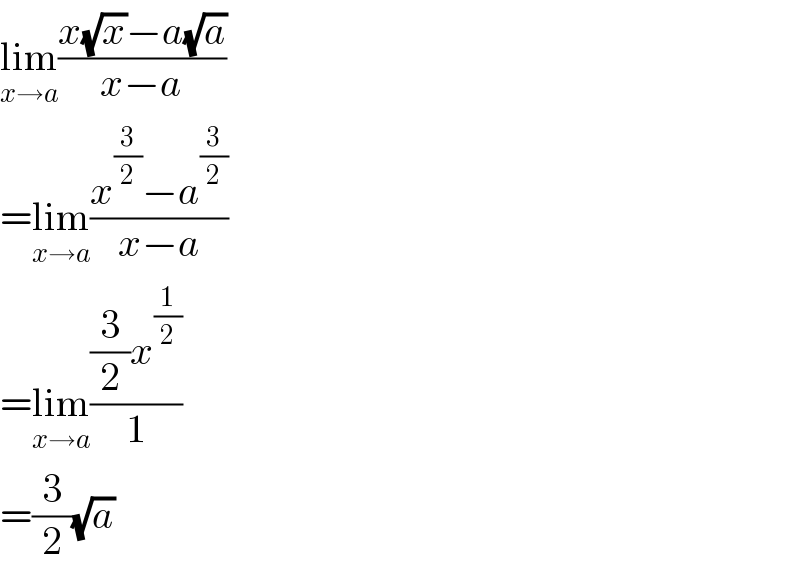
$$\underset{{x}\rightarrow{a}} {\mathrm{lim}}\frac{{x}\sqrt{{x}}−{a}\sqrt{{a}}}{{x}−{a}} \\ $$$$=\underset{{x}\rightarrow{a}} {\mathrm{lim}}\frac{{x}^{\frac{\mathrm{3}}{\mathrm{2}}} −{a}^{\frac{\mathrm{3}}{\mathrm{2}}} }{{x}−{a}}\: \\ $$$$=\underset{{x}\rightarrow{a}} {\mathrm{lim}}\frac{\frac{\mathrm{3}}{\mathrm{2}}{x}^{\frac{\mathrm{1}}{\mathrm{2}}} }{\mathrm{1}} \\ $$$$=\frac{\mathrm{3}}{\mathrm{2}}\sqrt{{a}} \\ $$
