Question Number 66683 by Tinkutara@ last updated on 18/Aug/19

Commented by mr W last updated on 18/Aug/19
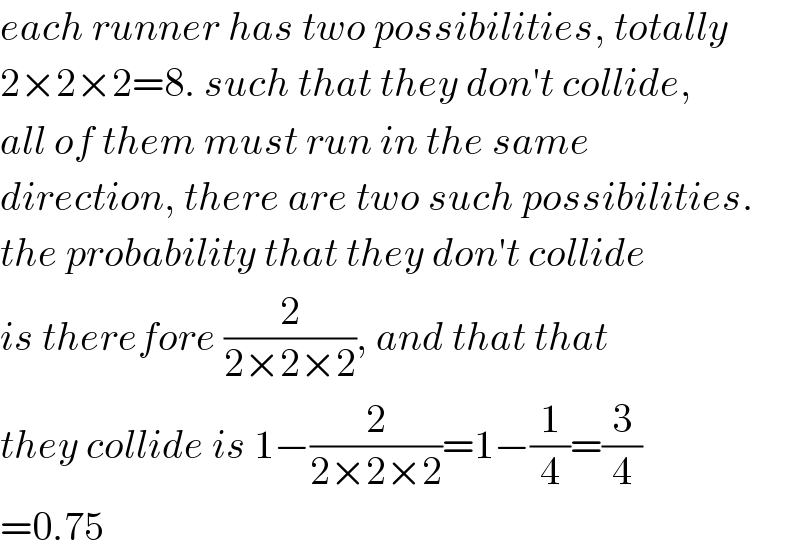
$${each}\:{runner}\:{has}\:{two}\:{possibilities},\:{totally} \\ $$$$\mathrm{2}×\mathrm{2}×\mathrm{2}=\mathrm{8}.\:{such}\:{that}\:{they}\:{don}'{t}\:{collide}, \\ $$$${all}\:{of}\:{them}\:{must}\:{run}\:{in}\:{the}\:{same} \\ $$$${direction},\:{there}\:{are}\:{two}\:{such}\:{possibilities}. \\ $$$${the}\:{probability}\:{that}\:{they}\:{don}'{t}\:{collide} \\ $$$${is}\:{therefore}\:\frac{\mathrm{2}}{\mathrm{2}×\mathrm{2}×\mathrm{2}},\:{and}\:{that}\:{that} \\ $$$${they}\:{collide}\:{is}\:\mathrm{1}−\frac{\mathrm{2}}{\mathrm{2}×\mathrm{2}×\mathrm{2}}=\mathrm{1}−\frac{\mathrm{1}}{\mathrm{4}}=\frac{\mathrm{3}}{\mathrm{4}} \\ $$$$=\mathrm{0}.\mathrm{75} \\ $$
Commented by Tinkutara@ last updated on 18/Aug/19

$${thanks}\:{sir}! \\ $$
Answered by JDamian last updated on 18/Aug/19

$$\mathrm{0}.\mathrm{75} \\ $$
