Question Number 66718 by otchereabdullai@gmail.com last updated on 18/Aug/19

Commented by Tony Lin last updated on 19/Aug/19
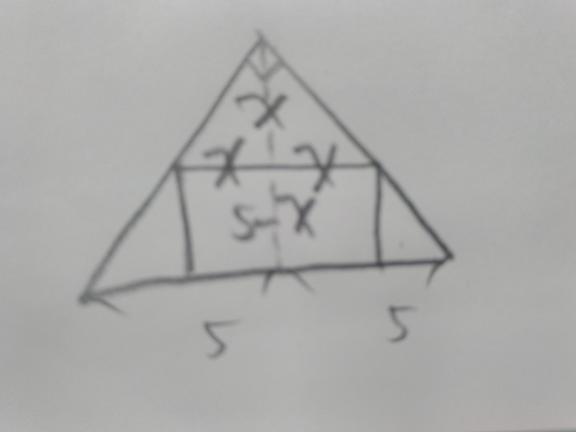
Commented by Tony Lin last updated on 19/Aug/19
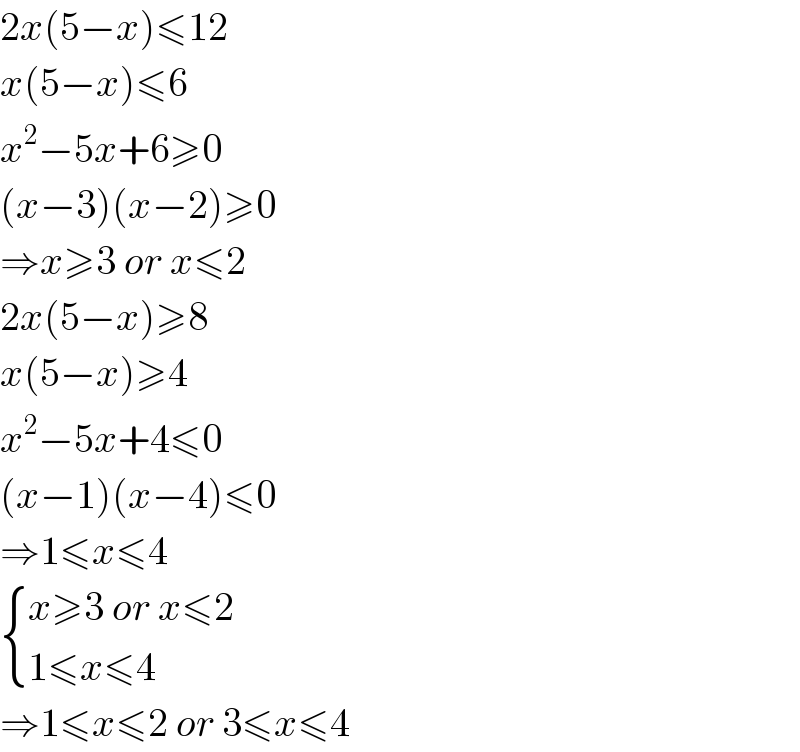
$$\mathrm{2}{x}\left(\mathrm{5}−{x}\right)\leqslant\mathrm{12} \\ $$$${x}\left(\mathrm{5}−{x}\right)\leqslant\mathrm{6} \\ $$$${x}^{\mathrm{2}} −\mathrm{5}{x}+\mathrm{6}\geqslant\mathrm{0} \\ $$$$\left({x}−\mathrm{3}\right)\left({x}−\mathrm{2}\right)\geqslant\mathrm{0} \\ $$$$\Rightarrow{x}\geqslant\mathrm{3}\:{or}\:{x}\leqslant\mathrm{2} \\ $$$$\mathrm{2}{x}\left(\mathrm{5}−{x}\right)\geqslant\mathrm{8} \\ $$$${x}\left(\mathrm{5}−{x}\right)\geqslant\mathrm{4} \\ $$$${x}^{\mathrm{2}} −\mathrm{5}{x}+\mathrm{4}\leqslant\mathrm{0} \\ $$$$\left({x}−\mathrm{1}\right)\left({x}−\mathrm{4}\right)\leqslant\mathrm{0} \\ $$$$\Rightarrow\mathrm{1}\leqslant{x}\leqslant\mathrm{4} \\ $$$$\begin{cases}{{x}\geqslant\mathrm{3}\:{or}\:{x}\leqslant\mathrm{2}}\\{\mathrm{1}\leqslant{x}\leqslant\mathrm{4}}\end{cases} \\ $$$$\Rightarrow\mathrm{1}\leqslant{x}\leqslant\mathrm{2}\:{or}\:\mathrm{3}\leqslant{x}\leqslant\mathrm{4} \\ $$
Commented by otchereabdullai@gmail.com last updated on 19/Aug/19
$$\mathrm{Thank}\:\mathrm{you}\:\mathrm{very}\:\mathrm{much}\:\mathrm{sir}! \\ $$
